智能电网数据挖掘及隐私保护方法研究

闫嵩琦

(国网陕西省电力公司 电力科学研究院， 西安 710000)

0 引言

近年来，随着智能电网建设力度的加大，产生了海量的用户用电数据信息，这些数据可以通过数据挖掘的方法反映出电力用户的用电习惯，从而给电网公司合理的制定供电计划提供支撑，但是传统的信息安全方法已不适用保障大数据时代数据的完整性，保密性，智能电网下的数据安全需要从全面进行考虑，包括供电设备，配电系统，数据采集系统，服务，管理等各个方面。所以，对智能电网数据挖掘及隐私保护进行研究对我国电网智能化的进程有重大意义[1-5]。

智能电网涉及了电力，控制，通信，计算机等领域，具有可靠性高，安全性高的特点。当在电网中检测到用户有异常能量消耗的时候，表明用户具有非日常用电活动，这就暴露了用户的隐私[6-7]。在电网数据挖掘之前进行隐私保护一方面可以保证数据挖掘的可靠性，另一方面又可以保护电力信息的隐私。

智能电网主要包括智能信息系统，智能计量系统，数据交易系统和智能服务系统[8]。智能计量系统指的是用户用电信息的统计，电网节点电压电流的记录等。智能信息系统用于电力系统中电力信息的采集，系统配置的功能[9]。智能服务系统用于为客户提供业务更改及查询等服务。数据交易系统用于实现数据信息的交换。

目前对于智能电网的隐私保护和数据挖掘的研究并不是很多，文献[10]针对智能电网的大数据安全和隐私保护问题，提出了加法秘密共享方案，并在安全聚合协议下汇总电表数据，该方法能够使电力公司在不泄露客户隐私信息的前提下提高服务质量[10]。文献[11]提出采用支持多属性泛化的随机化的隐私保护方法对电力数据进行保护，通过与传统的MBF算法进行对比，验证了所提方法隐私保护效率得到了大大提高[11]。

为了提高智能电网数据挖掘的效率并提高隐私保护性能，本文提出了采用熵差法对智能电网进行信息挖掘，采用HP滤波正则化方法对电网数据进行隐私保护。

1 基于熵差法的智能电网信息挖掘

在智能电网中，用户的隐私主要表现为用电信息及用户利益，智能电网的隐私维度一般包括以下四点[12-14]。

个人信息。个人信息包括身体，生理，住址，经济等各个方面，个人具有是否能让其他人访问个人信息的权利。

个人。指个人的身体情况，健康情况等。

个人行为。通过个人的活动总结的行为知识。

个人通信。指的是个人的通信受到相应的保护。

在智能电网中，个人信息包含了智能电表采集到的用户各种用电数据，包括了用电的时间，总量等[15]。电力用户具有这些数据信息使用情况的知情权。其他维度也会随着智能电网的数据采集而被采集，但与传统电网的其他维度信息一致，所以其他维度的信息也存在着安全隐患问题。所以智能电网与传统电网在数据挖掘上的区别在于智能电网的数据挖掘能够体现出用户的行为习惯，且一定要经过用户允许才能对其进行访问。

本文提出了基于内在模式和外在模式的熵差异常检测算法。熵差法借鉴了关键词检测方法，认为关键词会按照聚簇的形式出现，而普通词均匀出现。熵差法在电力用户异常行为中的应用则认为异常用电聚集在某一时间段，而平时为正常用电行为。采用熵差法时，熵值越大则不确定性越大，反之则越小。从统计上来看，聚集的簇和平均分布的组具有各自的分布特性，我们称之为内在模式和外在模式。内在模式体现了数据聚簇行为，外在模式表示聚簇消失的行为，两者的差值反映了数据的分布情况。在智能电网中将用户用电数据按时间戳进行划分，采用熵差法判别数据的聚类特性来确定异常点[16]。通常认为电力用户的用电情况是有规律的，当出现聚簇行为时认为是异常用电。求取过程如下所述。

1.数据量化。电力系统中采集上来的电力用户数据都是以时间为基准进行排列的，为了求取电力系统数的熵差，将数据进行空间划分，原本按秒为单位的数据划分成以分、小时为单位的数据。

2.求取熵差。对量化后的数据求取熵差，认为熵差值小的为正常点，熵差值较大的为异常点。假设某用电等级出现的位置为xi，求取过程表示为，假设平均距离为μ，则内部熵和外部熵表示如式(1)～式(3)。

dI={di|di<μ}

(1)

dE={di|di>μ}

(2)

S=v∩λ

di=xi+1-xi

(3)

求取同一等级用电量前后距离d，其内外熵表示如式(4)。

内部熵：

(4)

其中，Pd是d在dI发生的可能性,如式(5)。

外部熵：

(5)

其中，Pd是d在dE发生的可能性。

内部熵与外部熵的差值记作,如式(6)。

EDq(d)=(H(dI))q-(H(dE))q

(6)

对于日常非异常的用电等级，则其值均匀分布且满足如下条件,如式(7)。

P(d)=p(1-p)d-1

(7)

其中，p是用电等级出现的概率。对于服从几何分布的用电等级，熵差记为式(8)。

(8)

为了使均匀分布的用电等级得到稳定的熵，采用式(9)。

(9)

然后求取小时，分，秒的熵差异常点。并将不同等级的熵差结果进行排序，熵差值越大认为该点越有可能为异常值。

2 智能电网隐私保护

对电力用户数据进行数据挖掘之前，要保证用户的隐私信息不被泄露，也不能改变数据的性质。本文采用滤波器加正则的方法进行数据隐私保护。

2.1 HP滤波器

HP(High-Pass, HP)是基于时间序列的谱分析方法。将时间序列分成变化趋势分量τt和循环分量ct[17],如式(10)。

yt=τt+ct,t=1,2,…,T

(10)

采用最小化原理，将ct从yt中隔离,如式(11)。

(11)

其中，λ为惩罚参数。为方便求解，将HP滤波问题表示为式(12)。

(12)

M分别对x1,x2,…,xn求导，令导数为0，表示如式(13)。

X=[I+λF]-1Y

(13)

其中，I为单位矩阵，X为平滑后的数据，F表示为式(14)。

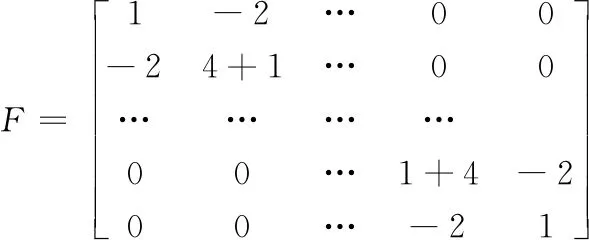
(14)

2.2 范数规则化

目标问题表示为式(15)。

(15)

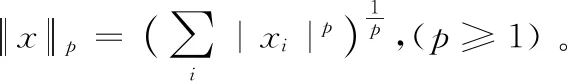
S={x|∀i,g(i)(x)=0 and ∀j,h(i)(x)≤0}

(16)

g(i)(x)是等式约束，h(i)(x)为不等式约束。对式(16)采用拉格朗日方法，求取目标函数f(x,y)与约束函数g(x,y)相切的点，如式(17)。

(17)

构造广义拉格朗日函数，λ和a为固定值,如式(18)。

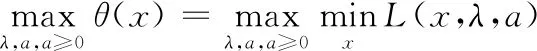
(18)

式(16)一定存在x使h(j)(x)<0。式(16)对所有待求项进行求导，导数为0则为正则化成立条件。

2.3 基于HP正则化的智能电网隐私保护

在HP滤波的基础上，引入正则化约束，建模过程如下所述。

1.将智能电网隐私保护问题转化为最小化问题，如式(19)。

(19)

2.KKT求解时要求矩阵正定，式(19)重写为式(20)。

(20)

K+F为正定矩阵。

3.用于电力用户的用电特征较少，认为用户行为是主要特征。用户的用电特征主要体现在，用电高峰，低谷。正则项约束的是用电数据的相似性，参数M为两天用电数据的距离,如式(21)。

(21)

X和Xt-1是第t天用电数据与第t-1天用电数据。

4.求解M与单位矩阵I的距离，距离越小则越相似,如式(22)。

(22)

则最终优化目标表示为式(23)。

s.t.X≥0,M≥0

(23)

令Q=I+λ(F+K),则有式(24)、式(25)。

(24)

(25)

a,β是正则参数，当迭代的X收敛认为是隐私保护后的用电量。

3 算例仿真

3.1 实验环境

为了验证本文所提的数据挖掘与隐私保护方法的可靠性，采用算例仿真，对其进行性能验证。实验环境如表1所示。

表1 实验环境

用于测试的智能电网数据集采集于某电力公司，包含电流电压等信息。用电数据主要为总体用电及用电器用电情况。

在对隐私数据进行挖掘时，还没有统一的评判标准，设数据集S，敏感数据为v，非敏感数据为λ，S=v∩λ。隐私测量指标定义为，当只给λ时，能够测量到隐私的可能性。分别采用标准差法，Z-Score C法，密度波动法对电网数据等级进行异常点挖掘并排序对比。选用不同的λ值，验证其对电网数据隐私保护的性质。

3.2 实验结果

根据以上的设计方法，分别计算四种方法的隐私得分，并进行量化处理，如图1所示。

由于电网数据集较多且数据中包含着异常点和非异常点。本文提取第20 000-40 000的数据，分别求取λ在不同值时的实验结果，如图2-图7所示。

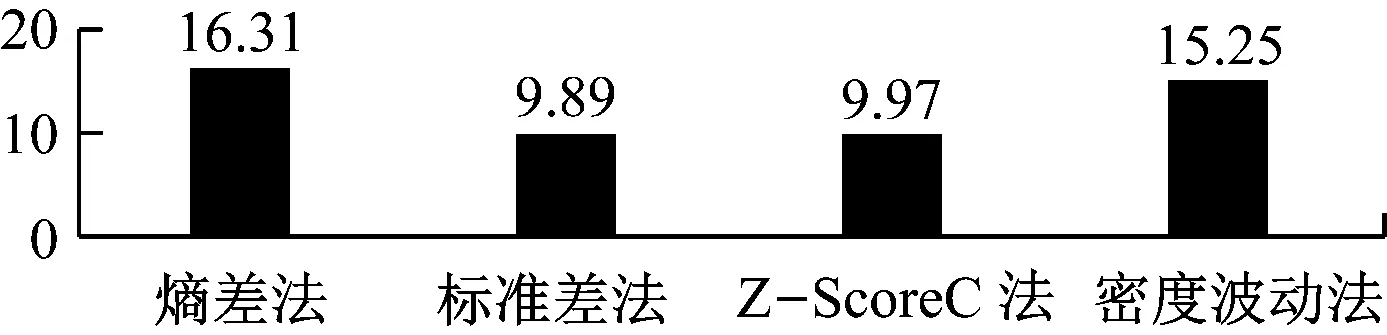
图1 隐私保护对比实验

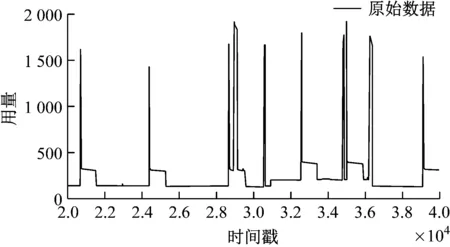
图2 原始数据

图3 λ=0.01的实验结果

图4 λ=0.05的实验结果

图5 λ=0.1的实验结果

图6 λ=0.5的实验结果

图7 λ=1的实验结果

3.3 结果分析

通过图1的隐私保护对比实验可以看出，熵差法在检测异常用电行为时，相比于标准差法，Z-Score C法和密度波动法均表现出了优势。在对某电网数据进行测试时，熵差法比标准差法提升了6.4，比Z-Score C提升了6.34，比密度波动法提升了1.06。当在电网数据隐私挖掘中找到的隐私数据越多，则越能为电网数据的隐私保护提供更高的保护，表明本文提出的熵差法在隐私保护中具有一定的优势。由图2-7所示可知，当λ取值在[0.5,1]的时候，能够更好的实现数据的保护功能，既能保护数据特征，又能实现与原始数据有很大的差异。

4 总结

本文提出了基于熵差法的智能电网数据挖掘方法及基于HP滤波正则化的隐私保护方法，对其数学模型进行了解析。通过熵差法的数据挖掘实验仿真，验证了熵差法比准差法，Z-Score C法，密度波动法具有更好的隐私挖掘效果，能够更好的识别隐私数据，为保障电网数据的隐私性提供了技术支持。采用HP滤波正则化方法对电网数据进行隐私保护，当选择合适的参数后，能够实现保证电网数据特征的前提下对电网数据进行隐私保护。实验验证了本文所提方法的可靠性及实用性。