离心风机流场大涡模拟与管中噪声数值预报

李亚，刘忠族 ，许影博 ，张楠

1船舶振动噪声重点实验室，江苏无锡214082

2中国船舶科学研究中心，江苏无锡214082

3中国船舶科学研究中心水动力学重点实验室，江苏无锡214082

0 引 言

离心风机管道中的噪声一般来源于叶轮辐射声、蜗壳和管道壁面边界层噪声、尾流场的湍流噪声、蜗壳和管道振动引起的噪声。噪声在离心风机管道中传播时，还会受到管道噪声模态的影响。另外，离心风机运行时，电机噪声和环境噪声也会传入管道。叶轮辐射声和壁面边界层噪声属于偶极子类型，辐射效率高于四极子类型的湍流噪声，离心风机振动噪声相比气动声小很多［1］。

将计算流体动力学（CFD）与计算声学相结合，可以进行气动噪声预报。Kato等［2］运用大涡模拟（Large Eddy Simulation，LES）方法得到叶片表面的脉动压力，采用Lighthill声类比理论计算远场辐射声。Younsi等［3］采用滑移网格方式及SST k-ω湍流模型计算了离心风机内部流场，利用非定常流场参数作为FW-H方程［4］输入项预报了辐射声。陈敏等［5］运用多块混合网格和动网格技术对螺旋桨的水动力性能进行大涡模拟，并结合FW-H方程预报了螺旋桨的低频流噪声。在上述噪声预报中，采用的是自由空间格林函数，其必须假设离心风机的几何尺寸满足声学紧致结构特征的要求。实际上，由于风机蜗壳和叶轮壁面的存在，机壳内部声源激发的噪声会在叶轮和蜗壳内壁面上发生多次反射及散射，最终通过风机进、出口向外辐射。

早在 1974 年，Moreland［6］就通过实验证实了蜗壳腔体结构对声波反射及散射会导致部分频段向外辐射的声功率大大增强。刘厚林等［7］采用大涡模拟方法获得了离心泵内部瞬态流场，在计算叶片表面偶极子辐射声场时，将叶片分为10个部分，分别积分得到3个方向的时域力，以此作为叶片旋转偶极子声源；以进、出口为吸声边界，其他壁面作为全反射壁面条件，声场计算结果与实验结果吻合良好。

离心风机形状复杂，过去流场模拟多采用非结构化网格，本文拟采用ICEM-CFD软件绘制结构化网格，使用Fluent软件模拟流场，通过得到的声源预报叶轮辐射声和壁面边界层这2种途径下的管道噪声，并将两者叠加结果与实际结果进行比较分析。

1 基于大涡模拟的风机流场模拟

1.1 模拟对象

计算对象为某型离心风机，如图1所示。离心风机重约117 kg，高约1.25 m；叶轮为后向叶轮，包含10个叶片，叶轮直径为503 mm；转速为1 470 r/min。采用管道进口、管道出口方式［8］对离心风机进行实验。进口管道与出口管道直径均为267 mm，进口管道长约12.3 m，出口管道长约11.6 m。测量情况如图2所示，其中传声器安装鼻锥，迎着来流，气体从鼻锥光顺地流过，可减少湍流脉动的影响。

图1 离心风机与叶轮Fig.1 Centrifugal fan and impeller

图2 离心风机噪声实验Fig.2 Noise measurement of the centrifugal fan

1.2 网格划分

根据实验中离心风机管道的连接情况，建立了整个流域的几何模型。流域含旋转叶轮，因此采用滑移网格方法模拟风机叶片的旋转运动：在风机叶片所在区域划分出一个小圆柱体区域（图3），部分管道伸入叶轮内部，导致交界面有阶梯。小圆柱体内包含叶片，此区域作为内域，为转动部分；其他区域作为外域，为静止部分。静止部分和转动部分设置交界面并进行数据交换，以此来保证各物理量守恒。

采用结构化网格形式划分网格，内域网格如图4所示；外域网格存在由方变圆段，无法保证结构化网格质量，因此也分为2部分，网格划分如图5所示。

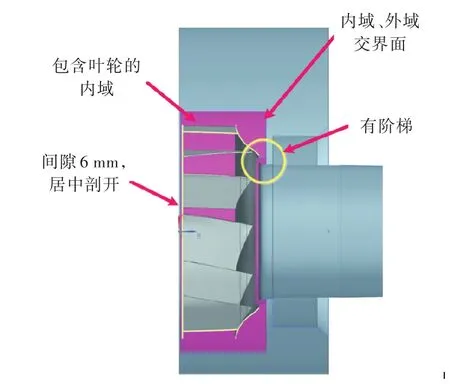
图3 交界面划分示意图Fig.3 Schematic diagram of interface division

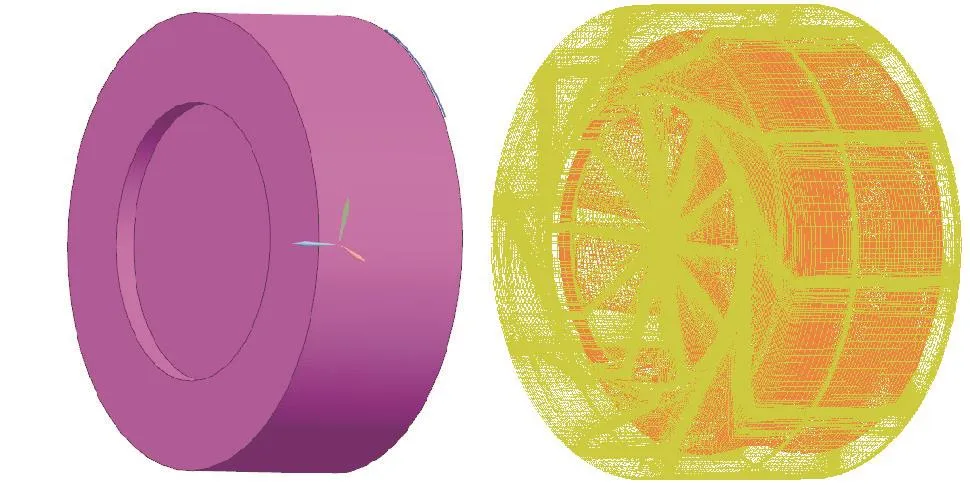
图4 风机内域结构化网格Fig.4 Structured grid of internal zone of the centrifugal fan

图5 风机外域结构化网格Fig.5 Structured grid of exterior zone of the centrifugal fan

在大涡模拟之前，采用划分方式相同而网格数量不同的多套网格（第1层网格厚度保持不变）进行稳态流场模拟，以出口流量为判据进行网格收敛性分析，考虑到大涡模拟网格数量要求以及单机计算能力，选取了其中1套网格：内域网格数为 5.19×106，蜗壳与管道网格数为 2.34×106，出口管道网格数为2.7×105；蜗壳第1层网格尺度设置为0.6 mm，叶片为0.3 mm，出口段为0.3 mm。在运算稳定后，无因次壁面法向高度 y+的范围为5～35，满足计算要求。

1.3 大涡模拟计算风机内部流场

湍流数值模拟方法可以分为直接数值模拟（DNS）方法和非直接数值模拟方法。大涡模拟既有直接模拟又有非直接模拟特征。它将流动分解为大、小2种尺度的湍流，对大尺度湍流进行直接模拟，而对小尺度湍流做近似处理。由于小尺度涡不直接依赖边界条件，而且一般具有各向同性性质，可以采用合适的湍流模型模拟。

大涡模拟计算对初始条件要求较高。首先采用RNG k-ε湍流模式下的结果作为初始条件，然后采用壁面自适应局部涡粘性（Wall-Adapting Local Eddy-viscosity，WALE）亚格子模型，进行大涡模拟计算，其中内域采用运动参考系。在计算稳定后，内域采用网格运动形式进行模拟，在运行一段时间后进行数据采集。数据采集的起始步数为第4 200步，对应时刻为0.105 s，采样间隔时间为2.5×10-5s。

叶轮旋转1/10周（即一个叶片旋转到上一个叶片位置）需要163步，1/10周再分为3个部分，分别绘制截面的压力分布云图，如图6所示。从图中可以看出，在计算过程中，叶片在不断旋转。在第4 212步与第4 374步，下一个叶片来到了同样位置，但叶轮附近的压力分布并不一致，这说明受涡流影响，叶轮所受压力并不是完全重复的。在第4 212步时，叶片离涡舌部位很近，气体受到挤压导致压强增大，叶片转过之后，压力下降。

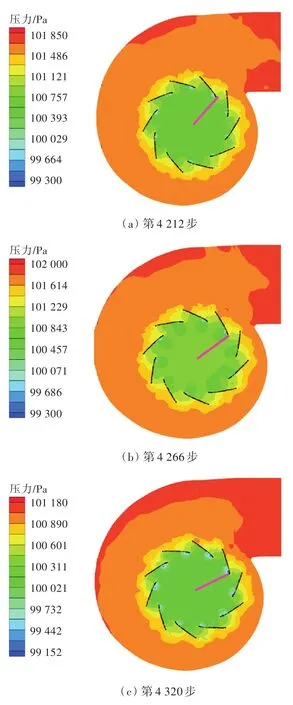
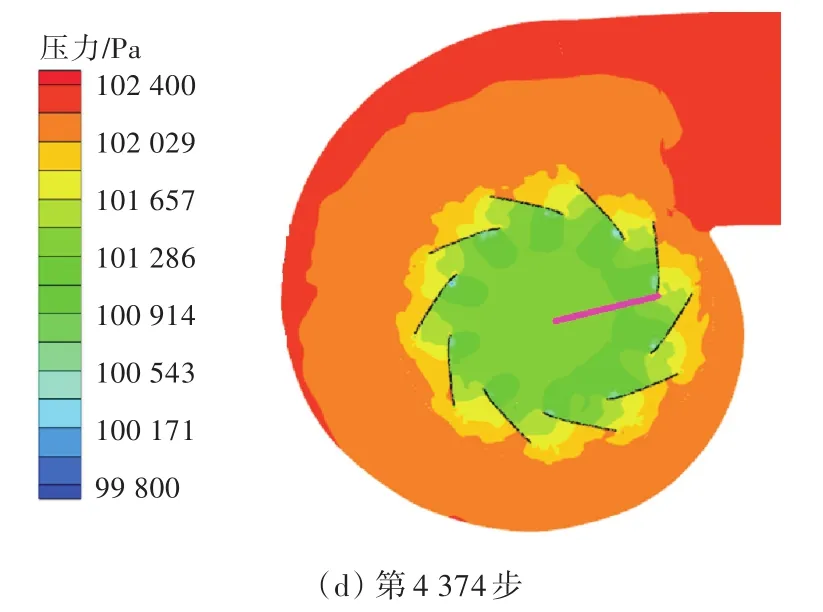
图6 叶轮旋转1/10周时流场绝对压力的变化Fig.6 Absolute pressure changes of flow field in the 1/10 cycle of impeller

2 离心风机管中噪声预报

离心风机管中噪声主要来源于旋转叶片的气动噪声，另外蜗壳表面压力脉动也会辐射噪声，这2个激励源均由大涡模拟计算得到。噪声在管中传播时还应考虑管道的影响。

2.1 叶轮辐射声计算

2.1.1 旋转噪声理论

首先，分析旋转机械在自由场的辐射声。叶轮工作时，叶片面元上会产生脉动压力，特别是在叶轮出口附近存在涡脱落时，压力脉动更明显，这些压力脉动会产生噪声。而且叶轮在不断旋转，因此叶轮噪声相当于旋转偶极子辐射声。

对于其中一块面元，F={Fx，Fy，Fz} ，可以得到各分力产生的总声压［9］：

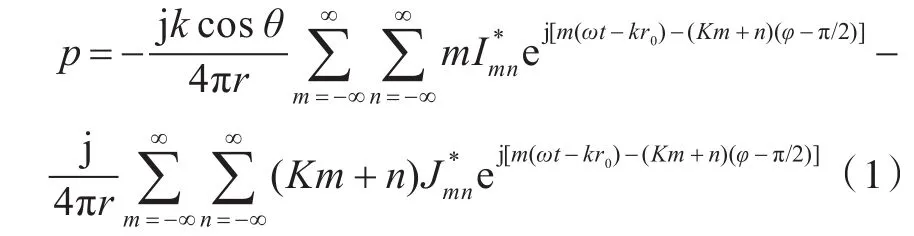
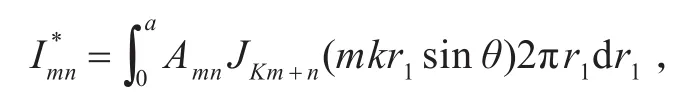
2.1.2 声学有限元计算原理

叶轮在蜗壳中旋转时，其噪声传播会受到管道声模态的影响。对于有限空间中的辐射声问题，一般采用边界元法或有限元法。边界元法尽管可以将维数降低，但求解速度慢［10］。声学有限元法的一般思路是：声场满足微分方程（含边界条件），可以构建与之等价的泛函，整个声场泛函可以用网格单元的形函数表达，对其求极值，即其变分为0，可以构建整体的矩阵方程。

在均匀介质、非粘性和绝热状态下，流体内的声学波动方程为

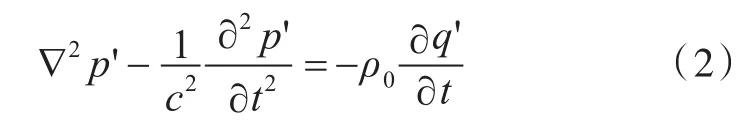
式中：ρ0为静态密度；c=ω/k。令声压p'=p(x，y，z)ejωt，声源q'=q(x，y，z)ejωt，代入式（2），得到Helmholtz方程：

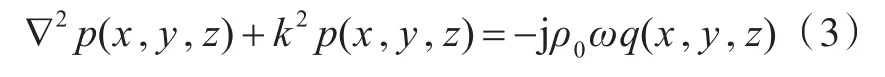
采用加权余量法，可以得到声场满足的矩阵方程［11］：

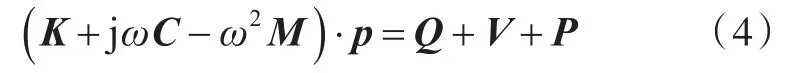
式中：K为声学刚度矩阵；C为声学阻尼矩阵；Μ为质量矩阵；p为声压向量；Q为声源向量；V为速度向量；P为输入声压向量。这些量均由计算域单元的形函数表达。

2.1.3 叶轮辐射声预报

采用大涡模拟计算叶轮旋转1周（从4200步到5831步）时的流场，输出了叶轮表面在每一步的受力情况，文件格式为计算流体力学通用符号系统数据（CFD General Notation System Data，CGNS）。在Virtual.Lab软件中导入相应文件，由于采用有限体积法计算得到的脉动压力结果存储在网格形心上，需要将形心结果传递到网格各节点［10］。经过传递，在某一时刻的压力云图如图7所示。

图7 第4 265步时叶片上的压力云图Fig.7 Pressure contours on impeller at the 4 265thstep

在Virtual.Lab软件中进行扇声源计算时，扇声源被当作一类专门的计算对象。将其叶轮等效为一个个旋转偶极子，即将叶片表面进行划分，得到的每个小区域相当于1个声源。声源数与计算的最高频率有关。图8（a）所示的彩色色块为在设置计算频率后叶轮表面区域自动划分的结果。然后，添加扇声源的边界条件，旋转速度设置为1 470 r/min，傅里叶变换加窗选择汉宁（Hanning）窗。图8（b）为叶轮旋转参数设置结果，由图可以看出旋转方向以及各个面积块的离散力分布。

图8 在Virtual.Lab软件中的叶轮设置Fig.8 Impeller setting in software Virtual.Lab

通常在划分声学有限元网格时，1个波长不少于6个单元，但由于外域尺度大，网格数量较多，计算时间长且对计算机硬件要求高，所以采用自适应阶次有限元（FEM Adaptive Order，FEMAO）算法，其主要原理是采用高阶多项式表达单元内的参数，比较粗糙的网格也能得到同样精度的计算结果［12］。

原来蜗壳入口处有部分伸到叶轮中，如图9（a）所示，这是由于蜗壳厚度为2 mm，而且有卷边。单个网格尺寸比较大，难以拟合其边界，导致网格生成质量不高，所以将卷起部分进行了简化，如图 9（b）所示。图9（c）为划分好的网格，其中网格均为四面体，单元最大边长为64 mm，网格数为12.9×104。

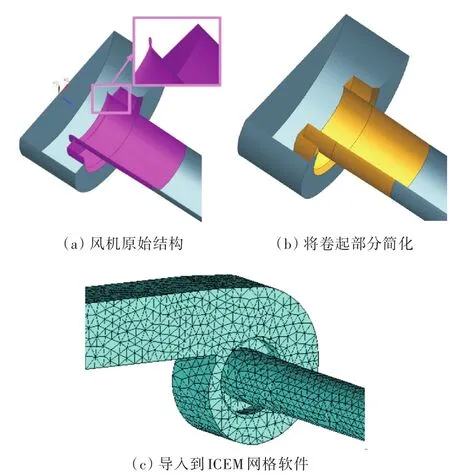
图9 声场区域网格划分过程Fig.9 Meshing process of sound field

进风管口与出风管口暴露在空气中，所以管口可作为无反射边界条件。在进、出风管口处的单元组上定义声阻抗来模拟无反射边界，将阻抗设置为416.5 N·s/m3。最大计算频率为6 kHz，频率间隔为24.5 Hz。求解场点坐标分别为：进风管（0 mm，0 mm，8 860 mm），出风管（-8 150 mm，368.7 mm，175.5 mm），这2点与实际测量点位置一样。图10为1/3倍频程噪声预报结果。由图可看出，噪声最大值为85 dB，进、出风管测点的噪声在高频时比较接近。

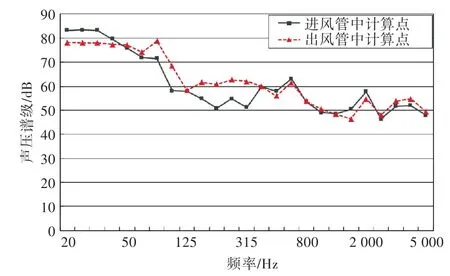
图10 叶轮辐射声预报结果Fig.10 Prediction results of impeller noise

2.2 蜗壳脉动压力辐射声计算

2.2.1 有固体壁面时湍流辐射声

当湍流区内存在刚性表面时，湍流区内的密度变化量可用Curle方程表示［13］：

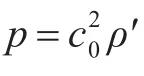
2.2.2 蜗壳壁面脉动压力辐射声预报

在大涡模拟时，蜗壳表面力无法同时输出，可以采用另外一种软件操作方法：即输出计算过程中整体域的解，文件格式仍为CGNS。由于输出文件包含了整个流体域的结果，自然也包括蜗壳与管道界面的结果。采用该方法后，每个文件均较大，因此步长增加1倍，为5×10-5s。数值计算从第4 200步开始，共计算816步，即叶轮旋转1周。

管道内表面是光顺的，湍流强度低，仅产生边界层的噪声，且该噪声的量级很低；而蜗壳内表面有大量的涡分离，所以本次只对蜗壳内表面部分进行积分计算。

数据存储于体单元中，实际计算只需要蜗壳表面网格上的数据，所以要进行数据传递。流场计算时的网格较密，而壳体单元组的网格较稀疏，本文采用无能量损失算法（Conservative Maximum Distance）将力从流体网格映射到蜗壳壳体网格。在CFD时域计算时，考虑到声学分析需要，对其进行快速傅里叶变换，图11为150 Hz时的脉动压力云图。

图11 150 Hz时的蜗壳壁面脉动压力云图Fig.11 Pressure fluctuation contours of volute wall at 150 Hz

同样，在入口单元和出口单元组分别定义无反射边界条件，将完成数据传递后的结果作为边界条件，物理类型为表面偶极子（Surface Dipole）。最大计算频率6 kHz，频率间隔为25 Hz。1/3倍频程噪声计算结果如图12所示。由图12的噪声预报结果可以看出，不同位置处的辐射声在低频时有差别、在高频时趋于一致。

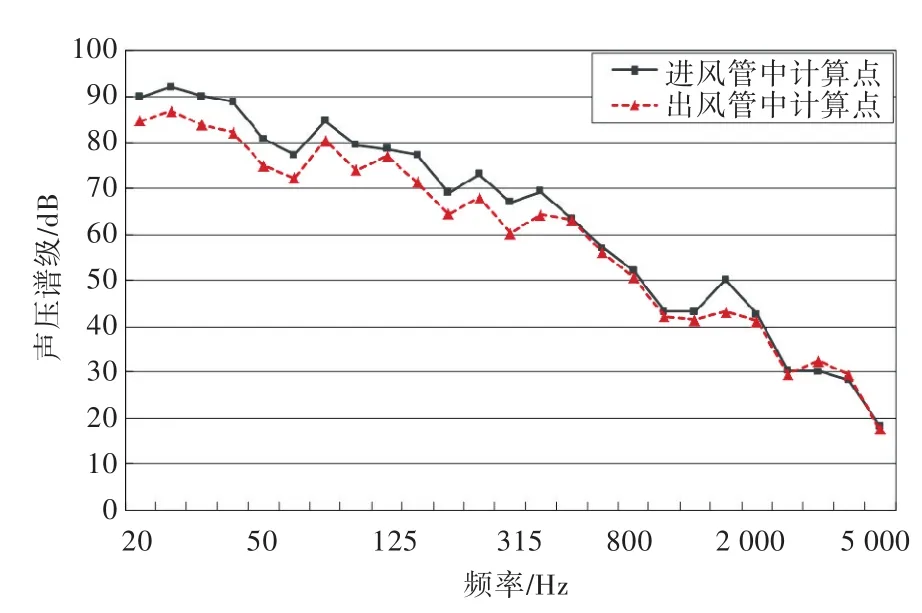
图12 蜗壳壁面脉动压力辐射声预报结果Fig.12 Prediction results of volute wall pressure fluctuation noise

3 风机管中噪声计算结果

3.1 进风管中叶轮辐射声与蜗壳壁面脉动压力辐射声对比

图13为前述进风管中叶轮辐射声与蜗壳壁面脉动压力辐射声的对比结果。由图可以看出，进风管内蜗壳流噪声在低频部分高于叶轮辐射声，而在高频时又低于叶轮辐射声。这表明叶轮和蜗壳壁面的非定常力是离心风机最主要的气动噪声源，证实了文献［14］中的结论。

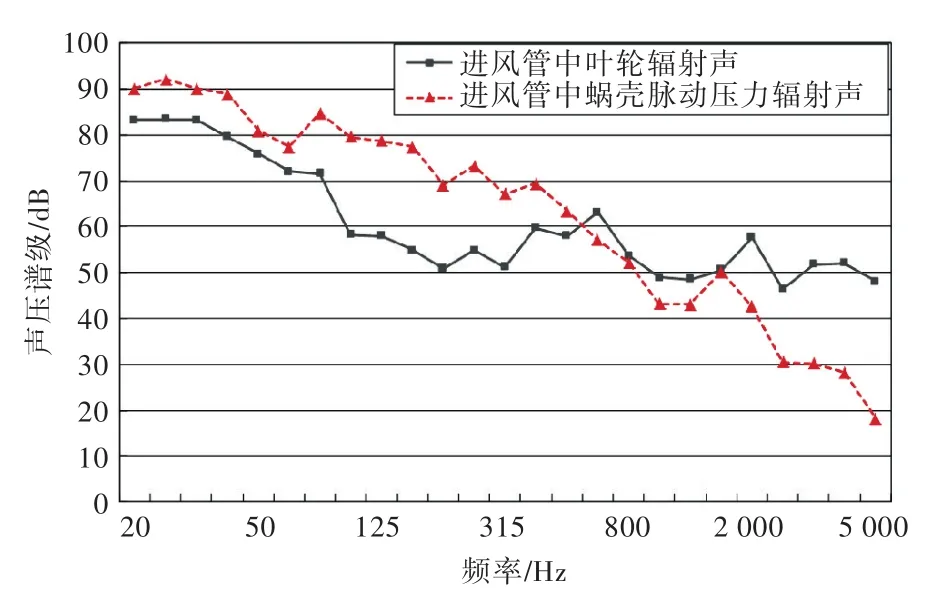
图13 进风管中叶轮辐射声与蜗壳脉动压力辐射声的对比结果Fig.13 Contrast between impeller noise and volute pressure fluctuation noise

一般叶片噪声较大，但本例中离心风机叶轮与蜗壳距离非常近，在蜗舌部位距离仅有28.5 mm，表明分离的涡（脱离涡将造成较大的脉动，从而产生较大辐射声）尾流还会直接作用于蜗壳表面。另外，从声源作用面积来讲，10个叶片的总面积（含叶面和叶背2面）为0.36 m2，而蜗壳内表面面积为2.2 m2，后者远大于前者。这些因素导致蜗壳内流噪声较大。但高频部分叶轮辐射声又增加了，这部分跟直接涡发放有关。在大于临界雷诺数（Re＞2×106）情况下，叶片涡的发放频率满足以下公式［15］：

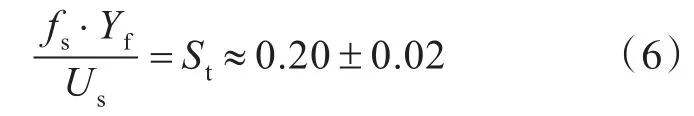
式中：Yf为靠近叶片出气边处尾流的剪切层厚度，实际相当于涡街的横向宽度；Us为出气边处的切向速度，St为斯特劳哈尔数。由于叶片为厚2.5 mm的直平头，Yf厚度为2.25 mm；叶轮出气边速度由流场得到，约为38 m/s，由此得到涡发放频率为3 378 Hz。一般在涡发放频率附近的噪声会明显增高，由图13可知，在3 150～4 000 Hz中心频段处噪声级较大，跟3 378 Hz这一频率吻合。

3.2 计算结果与实验验证

叶轮与蜗壳表面脉动力虽然从同一时刻开始计算，但步长不一样，所以将他们当作无规相位声波进行叠加，并对比叠加结果与实验结果（图14），由图可以看出，与试验结果相比，数值计算结果在中低频处偏低，在高频处有点偏高，最大偏差约14 dB，两者整体趋势一致。

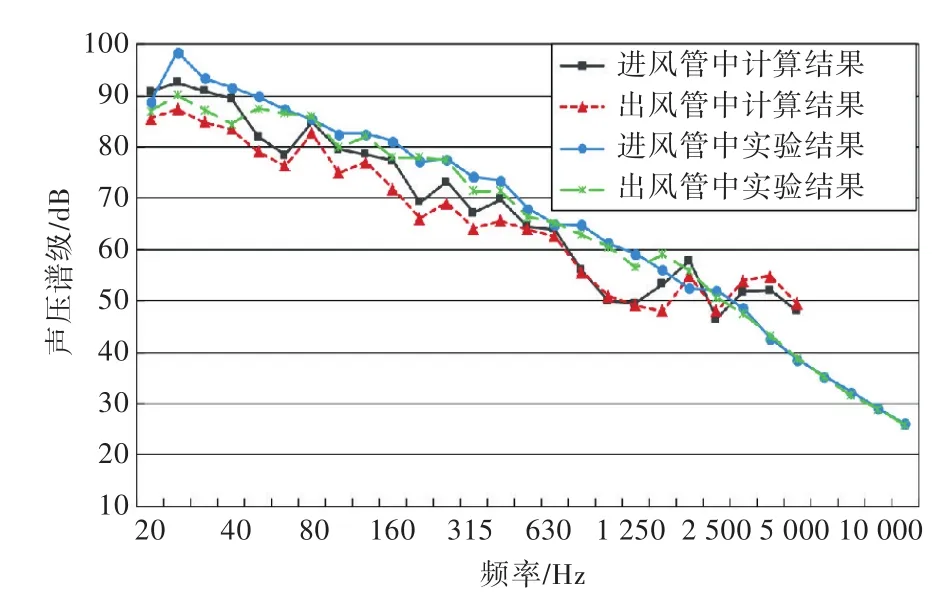
图14 实验结果与数值计算结果对比Fig.14 Comparison between experimental results and predicted results

数值计算结果的精度与整个预报过程的每个环节都有关系：在流域建模、流场预报、辐射声预报都会存在影响。其中流场预报时与网格个数、交界面设置（由于内域旋转需设置此项）、大涡模拟计算本身精度有关；声学计算只考虑力源项的结果，采用软件Virtual.Lab求解时，将叶轮表面划分为上千个集中面源，这也降低了精度。另外，由图14还可以看出，预报结果出现了较多的尖峰，这与采样时间短、在计算时没有将采样结果当作随机信号有关。而且叶轮对声场的反射无法计算，流速对声传播的影响也未考虑。

4 结 论

本文采用结构化网格，使用大涡模拟方法获得了离心风机流场多个时刻的压力分布，分别计算了风机管中叶轮辐射声和蜗壳脉动压力辐射声，得出以下结论：

1）叶轮辐射声和蜗壳脉动压力辐射噪声相比，在低频时前者明显低于后者，这与蜗壳辐射声面积较大有关；在高频时前者又会高于后者，这与叶片较强的涡发放有关。

2）与噪声实验结果相比，噪声数值计算结果在低频时偏低，在高频时偏高，两者整体趋势基本一致，能够满足工程分析需要。

3）数值计算结果与实验结果较吻合，验证了叶轮辐射声和蜗壳压力脉动辐射噪声预报方法的有效性，也从侧面反映出两者是管中噪声主要的噪声源。