舱室复合材料结构的抗爆性能数值仿真

吴广明，许亚东，李正国，王志凯，姚熊亮

1中国舰船研究设计中心，上海201108

2哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

0 引 言

战斗部舱内爆炸是水面舰艇生命力的重要威胁之一。对于战斗部舱内爆炸，舱室除了受高温、高压气体产生的局部破坏外，还会使破片对舱室围壁产生侵彻破坏，导致舱内人员和设备等无法正常工作［1-3］。因此，研究舱内爆炸作用下的破坏作用及防护结构的防护效果，对减少爆炸产物对舱室人员和设备的损伤具有十分重要的意义。玻璃纤维是抗爆防护领域最早应用的复合材料，具有质量轻、抗侵彻性能好及冲击波吸收效率高等优点，这对于舰船抵抗爆炸冲击、保温隔热及抗侵彻具有重要意义［4］。凯夫拉是一种新型合成纤维，其强度是普通钢的5～6倍，韧性是普通钢的2倍，密度约为钢材的1/6，且在高温下能够保持良好的力学性能，目前已逐渐成为舱室重要的防护材料［5］。

本文将采用LS-DYNA有限元软件，首先建立凯夫拉/钢板结构的有限元模型，并根据文献［6］中的实验结果验证本文建模方法，验证计算凯夫拉板和钢板局部破坏响应问题的准确性。然后，在此基础上将凯夫拉材料应用于复杂船体模型上，研究该材料对冲击波的吸收效果，计算凯夫拉/钢板结构在爆炸载荷作用下的动态响应。

1 模型与方法

1.1 流固耦合算法理论

在LS-DYNA有限元分析中，采用任意拉格朗日—欧拉（ALE）流固耦合算法，计算舱室内板架在爆载荷作用下的变形情况。ALE法避开了单一拉格朗日算法或单一欧拉算法的缺点，其将物理量定义在任意运动的网格上，可处理运动边界和大变形问题［7］。在流固耦合算法中，炸药和流场为ALE单元。在拉格朗日网格当中，1个单元中只能存在1种物质，而对于ALE网格，1个单元中最多能存在7种物质，本文利用*ALE_MULTI_MATERIAL_GROUP将炸药和流场这2种材料的单元定义为多物质材料耦合网格单元类型。舱室结构为拉格朗日单元，通过关键字*CONSTRAINED_LAGRANGE_IN_SOLID对结构、流场及炸药进行耦合。

1.2 几何模型及边界条件

船体有限元模型主要由板单元与梁单元构成，其中板单元主要包括甲板、舷侧板、横舱壁等，梁单元主要包括横梁、纵骨及舱壁桁材等，船体网格大小为0.2 m。本文选取典型的船舯三舱段模型为研究对象，对于垂向1甲板和2甲板间、图1所示舱壁四周，铺设厚20 mm的芳纶材料，采用5层实体单元建立装甲防护层，对舱室围壁上单元节点与凯夫拉材料单元节点采用tie约束，当应变达到0.25时，约束失效。需确保钢材和装甲结构同时受到冲击波的破坏作用。TNT当量为100 kg，爆心位置选取在舱室中心的横舱壁与纵舱壁交界处，炸药爆心位置如图1所示，舱室装甲防护结构如图2所示，具体工况如表1所示。

图1 药包位置平面布置图Fig.1 The plan of TNT charges positions

图2 舱室装甲防护结构有限元模型Fig.2 FE cabin model of armored protection structure

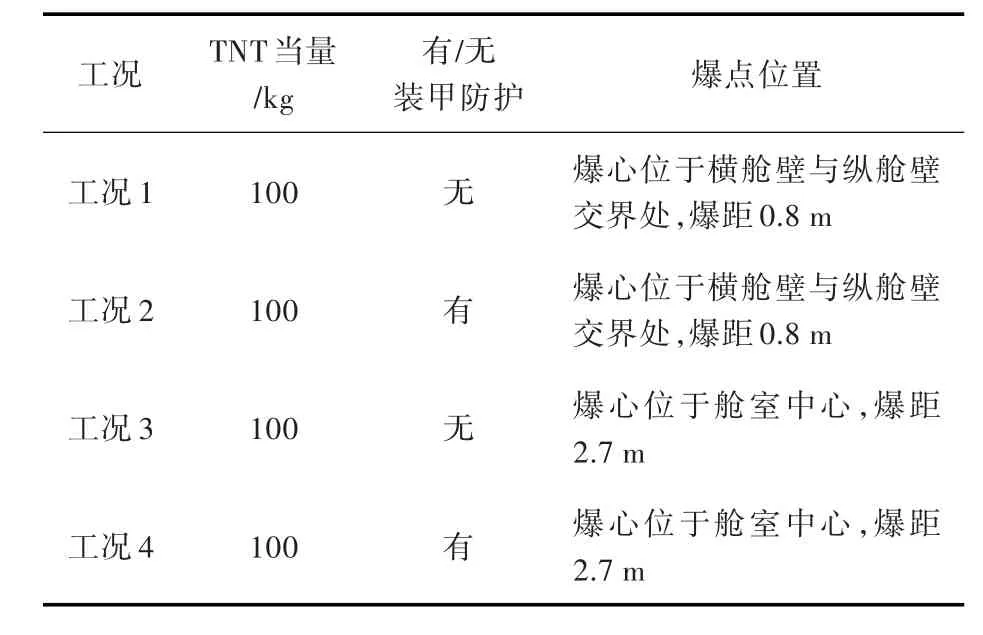
表1 工况设置Table 1 Working condition setting

1.3 模型材料参数

1.3.1 凯夫拉材料参数

凯夫拉纤维采用拉格朗日八节点六面体实体单元建模。本构关系采用材料库中关键字*MAT_COMPOSITE_DAMAGE对凯夫拉材料正交各向异性的弹性材料进行定义，并使用*MAT_ADD_EROSION对材料的失效进行定义。根据文献［8］，给出凯夫拉复合纤维材料的具体参数如表2所示。其中，E11，E22和E33为材料3个方向的杨氏模量，G12，G13和G23为材料3个方向的剪切模量。

表2 凯夫拉材料参数Table 2 Parameters of Kevlar fiber material

1.3.2 空气域及药包参数的确定

相关资料显示，目前反舰导弹多以近似圆柱形装药为主，且柱形装药由于长径比变化多，爆炸后压力场的分布规律也比较复杂。由于本文研究不考虑爆源形状对毁伤结果的影响，为此，借鉴Hammond［9］关于柱形装药与等质量球形装药等效性的研究成果，将柱形装药简化为球形装药，装药和空气单元均采用欧拉单元，船体结构采用拉格朗日单元，并通过采用Van Leer+HIS（二阶精度）方法进行计算，以提高模型的计算精度。当TNT当量为100 kg时，计算得出药包半径为0.24 m，空气模型为49倍药包半径的球形区域。为精细捕捉冲击波传播规律并节省计算时间，划分网格时采用渐变式网格，空气流场与炸药实体单元接触处网格大小为0.01 m，最外侧流场的网格尺寸与舱段网格尺寸相近，大小约为0.3 m，采用关键字*BOUNDARY_NON_REFLECTING模拟无限流场，以此来避免流场边界对空气流场的反射作用。炸药和1/8个空气流场有限元模型如图3所示。

图3 1/8个空气流场有限元模型Fig.3 FE model of 1/8 air flow field

采用关键字*MAT_high_explosive_burn模拟炸药模型，采用*EOS_JWL模拟炸药状态方程，相关参数见表3。JWL状态方程如式（1）所示［10］：

式中：P和V0分别为爆轰产物的压力与初始相对体积；E0为单位体积炸药的初始内能；A，B，R1，R2，ω为与炸药性质相关的常数；e为自然数。

表3 炸药状态方程参数Table 3 Parameters of explosives state equation

采用关键字*MAT_null材料模型模拟流场，采用*EOS_linear_polynormal模拟空气状态方程，相关参数见表4。线性多项式状态方程如式（2）所示［8］：

式中，C0～C6为该线性多项式状态方程系数，针对不同的流体状态方程，取不同值；E为单位体积内能；μ=ρa/ρ0-1，为密度比系数，其中 ρa为空气密度，ρ0为参考密度。

表4 流场状态方程参数Table 4 Parameters of flow field state equation

考虑材料应变率敏感性的本构方程有很多，本次采用与实验数据吻合较好的Cowper-Symonds模型来充当结构材料，材料相关参数如表5所示。

表5 钢材料状态方程参数Table 5 Parameters of steel material state equation

本文根据舱室结构，利用通用有限元软件ANSYS进行建模，模型主要由板单元与梁单元构成。所用材料屈服强度均为390 MPa［11］。爆炸载荷与船体结构的耦合关系采用ALE算法计算，通过关键字*CONSTRAINED_LAGRANG E_IN_SOLID定义船体舱段结构与药包空气的耦合关系，采用*CONTACT_AUTOMATIC_GEN ERAL模拟爆炸过程中船体结构间的相互接触。船体舱段长13 m、宽12.5 m、高13 m，空气流场半径12 m。对于船体结构，采用 PLASTIC_KINEMATIC模型［12］计算，并计及了材料的应变率效应影响。由于舱室内爆结构会产生高应变率响应的情况，故需合理考虑材料应变率效应对材料造成破坏所带来的影响，同时通过等效失效应变定义材料的失效，并根据文献［13］取材料的失效应变为0.25。

1.4 模型验证

采用文献［6］中公布的实验结果，验证上述数值计算方法的有效性。图4所示为在近场爆炸冲击载荷作用下，根据钢板/芳纶复合材料双层防护结构防爆性能数值计算得到的钢板和芳纶的变形模式，并与实验结果进行对比。模型验证采用的芳纶复合材料参数如表6所示。

数值结果与实验结果的对比如表7所示。从表7中可以看出，采用实验和数值这2种方法，钢板和芳纶复合材料均发生了穿孔和背面开裂现象，破损区域呈正方形，芳纶复合材料还伴随分层现象。图4中，钢板和凯夫拉板均产生了破口，并沿背板方向出现了弯曲变形。实验中，钢板的破口尺寸为13 mm×13 mm，钢板背板凸起高度为16 mm，凯夫拉背板凸起高度为17 mm；数值模拟钢板的破口尺寸为12.7 mm×12.7 mm，钢板背板凸起高度为14.6 mm，凯夫拉背板凸起高度为15.8 mm，误差均在10%以内。可见，钢板/芳纶复合材料双层防护结构抗爆性能数值模拟结果与实验结果吻合较好，验证了本文数值计算方法的有效性。

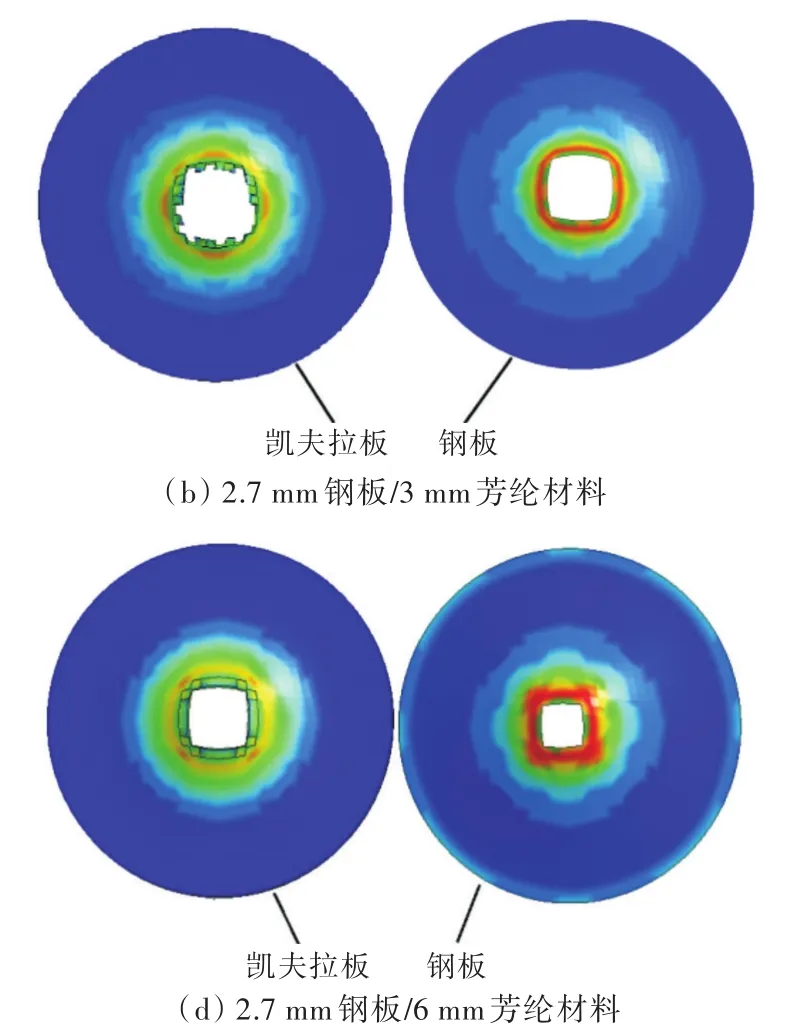
图4 不同厚度芳纶防护材料损伤情况Fig.4 Damage of aramid protection materials with different thickness

表6 芳纶复合材料参数Table 6 Parameters of aramid fiber composites

表7 抗爆特性的数值与实验结果对比Table 7 Comparison of damage features between numerical and testing results

2 计算结果分析

2.1 爆炸冲击波传播分析

载荷是一切物理过程计算的基础，载荷输入正确，才能保证计算结果的精确性。因此，本节将流场压力载荷与经验公式进行对比，以保证所建流场及炸药模型输入的正确性。在自由场爆炸领域，国内外学者基于大量的实验，通过实验研究和理论推导提出了一系列TNT冲击波超压峰值计算公式。其中，亨利奇公式［14］以大量的实验为基础，使用范围较广，可信度较高。通过有限元软件计算了TNT当量为100 kg时，在自由场中存在平板的爆炸冲击波时历曲线，如图5所示，并与亨利奇公式行了对比分析。亨利奇公式如式（3）所示：

图5 100 kg TNT药量下的冲击波时历曲线Fig.5 Time history curves of shock wave for 100 kg TNT charge

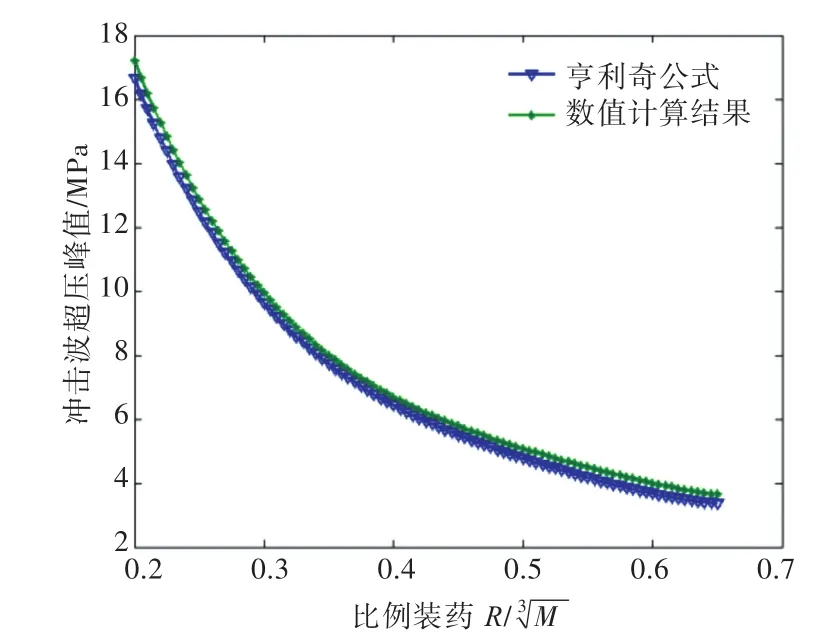
图6 100 kg TNT药量下冲击波峰值压力Fig.6 Peak pressure of shock wave for 100 kg TNT charge

2.2 舱室毁伤效果

数值计算中，采用100 kg TNT当量的球形药包在舱室引爆，爆点分别位于舱室中心的中纵剖面横舱壁与纵桁交界处以及舱室中心。利用LS-DYNA有限元软件自带的后处理器，提取典型位置的毁伤效果，如图7～图10所示。

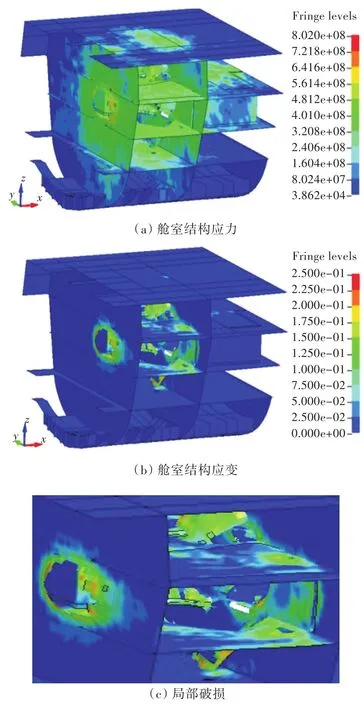
图7 工况1舱室内爆局部结构破坏云图Fig.7 Partial structure damage contours of internal explosion under condition 1

图8 工况2舱室内爆局部结构破坏云图Fig.8 Partial structure damage contours of internal explosion under condition 2

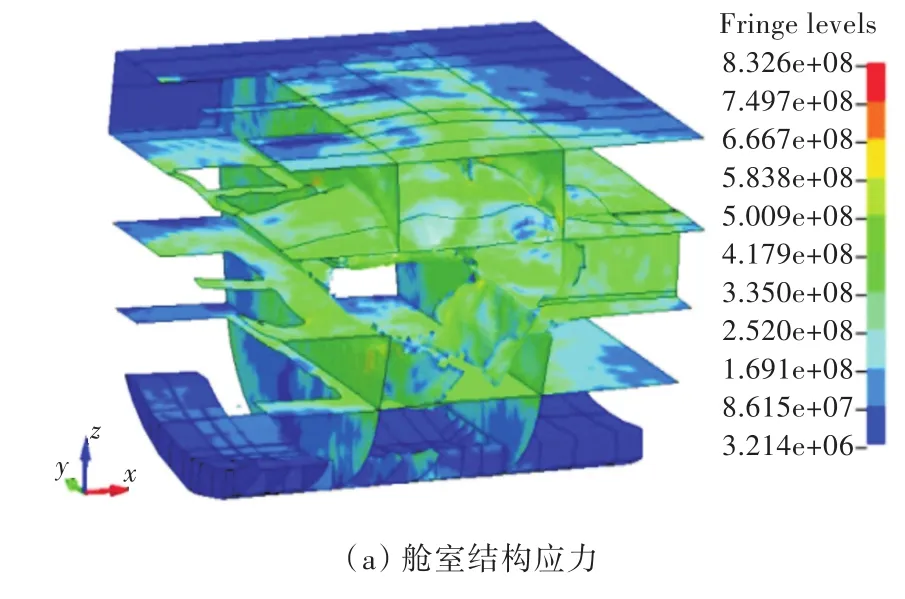
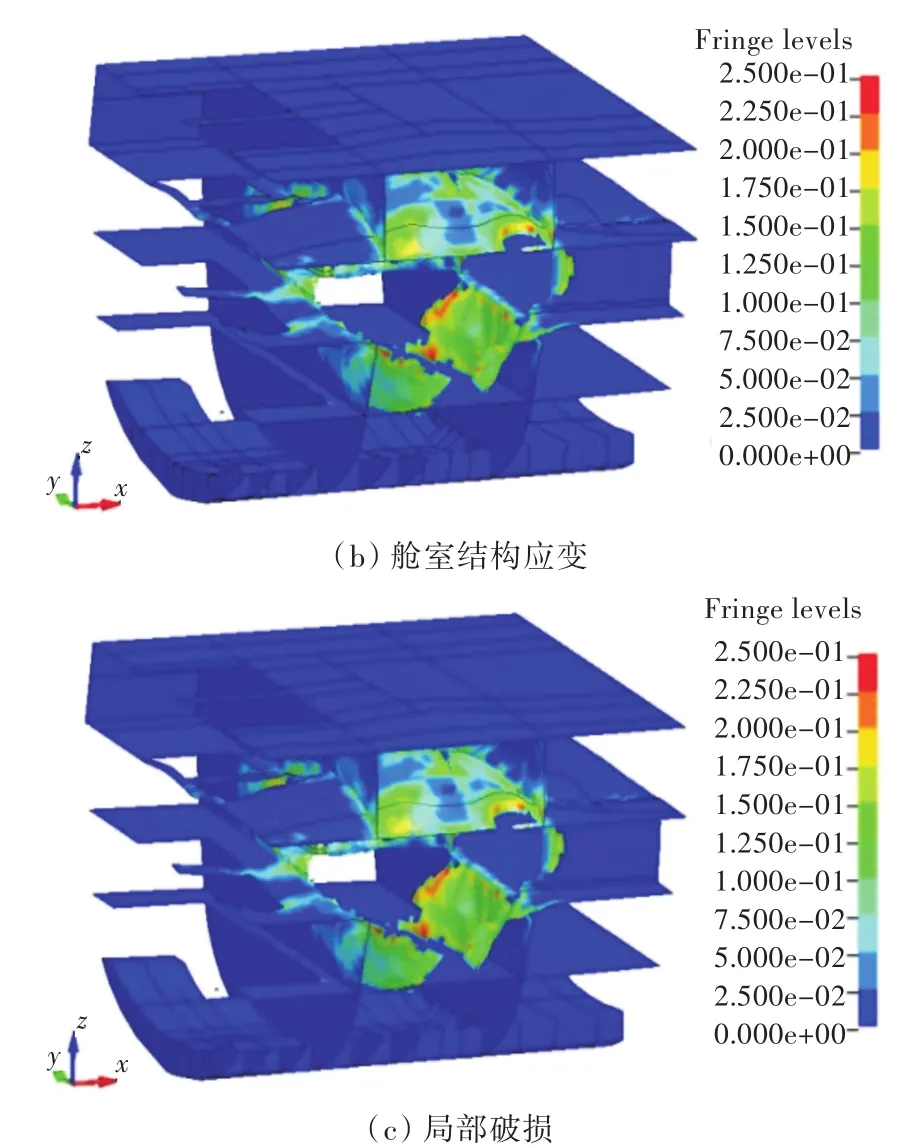
图9 工况3舱室内爆局部结构破坏云图Fig.9 Partial structure damage contours of internal explosion under condition 3

图7、图8（a）和图8（b）所示为船体结构的米赛斯应力及塑性应变云图。冲击波以球面波的形式作用在结构上，在距离较近的位置首先产生破口和塑性区域；与药包邻近的甲板和舱壁结构在瞬态强冲击载荷作用下，材料失效形成破口。然后，随着时间的推移，距离药包较远的结构相继受到冲击波和应力波的作用。由于冲击波能在空气中传播，在结构上具有透射反射等作用，因而冲击波能量衰减速度较快，导致在应力云图区域形成了以药包中心为球心的球形区域。对于舱室内爆工况，只在爆炸舱室周围产生了明显的塑性变形，较远位置则未发生塑性变形。这是由于空气具有较强的可压缩性，冲击波能量耗散较快，且药包附近结构吸收了大量冲击波能，导致较远处结构受力较小，只发生了弹性振动，未产生塑性变形。图中，应变云图呈现为蓝色，说明空中接触爆炸具有明显的局部效应。

图8（c）和图 8（d）所示为凯夫拉材料在爆炸载荷作用下的米赛斯应力云图及位移云图。从图中可以看出，凯夫拉材料发生了严重的扭曲变形，部分单元失效；米赛斯应力小于结构上的应力，凯夫拉板和钢板同时受到瞬态强冲击载荷作用，产生破损。由于钢板密度 ρs=7 800 kg/m3，弹性波速cs≈5 000 m/s；凯夫拉密度 ρk=1 200 kg/m3，弹性波速ck≈2 510 m/s，冲击波穿透钢板的透射系数η=2/(1+ρscs/ρkck)=0.14＜1，由此说明，冲击波透过钢板进入凯夫拉材料时强度是逐渐减弱的。冲击波是先到达钢板，经钢板透射再到达凯夫拉材料，这样一方面冲击波的强度会减弱，另一方面凭借凯夫拉材料的强抗拉伸能力，也能有效避免其背面的设备以及人员受到严重损伤。

图9、图 10（a）和图 10（b）所示为船体结构的米赛斯应力及塑性应变云图。由于药包位于舱室中心，开始时爆炸舱室周围舱壁均未发生破坏，舱室板架结构在板架和角隅处冲击波的多次反射作用下，在强、弱构件交接处明显发生撕裂现象。

未采用防护材料的横舱壁受到爆炸载荷作用后发生了完全撕裂破坏，而采用了防护材料的横舱壁则只在冲击波正对位置产生了部分撕裂破坏。对比工况3和工况4可以发现，没有铺设防护层的舱壁和甲板均有一定的破坏，且破坏程度相差不大，而有防护结构的舱壁破坏则较轻。

图10（c）和图 10（d）为凯夫拉材料受爆炸载荷作用后的米赛斯应力云图及位移云图。凯夫拉材料的抗拉强度很大，可以达到3.9 GPa，而在该过程中，所受最大等效应力为191 MPa，没有产生失效破坏。

通过对工况1～工况4进行的数值计算，可以得到不同位置处破口和塑性应变区的尺寸如表8所示。

表8 不同位置的破口和塑性应变区尺寸Table 8 Sizes of crevasse and plastic strain zones at different positions

3 结 论

本文采用LS-DYNA有限元软件，对铺设凯夫拉防护材料的舰船舱段在舱室内爆载荷作用下的动态响应进行了数值模拟研究，通过对比舰船结构在不同爆炸工况下的数值，得出以下主要结论：

1）通过模拟自由场中冲击波的传播规律，以及与装甲钢板/芳纶复合材料双层防护结构防爆轰实验的对比验证LS-DYNA有限元软件ALE模块可模拟炸药、空气、结构间的耦合关系以及结构的破坏形式。

2）对于舱室内爆，在强、弱构件交界处，由于存在冲击波反射作用，故会产生应力集中现象，进而产生撕裂现象或破口破坏，其为舱室结构的薄弱环节。

3）当爆心位于舱室中心时，对舱壁周围的破坏较严重。由于当爆心离舱壁较近时，结构在很短时间内会发生破坏并产生破口，破口能起到很好的泻压作用。高温、高压气体向舱室周围流动能够有效减小准静态压力对结构的破坏作用，因此，在适当位置增设泻爆孔能够有效减小空爆载荷的破坏作用。

4）本文通过数值计算，给出了舱内爆炸舱壁、甲板等处破口及塑性区的尺寸，能为舱内爆炸的毁伤效果提供参考，更准确的结果还有待舱室爆炸模型实验的验证。