内爆炸后燃烧反应率时间历程理论预估及能量释放常数确定方法

徐维铮，吴卫国 ，况正

1高性能舰船技术教育部重点实验室，湖北武汉430063

2武汉理工大学交通学院，湖北武汉430063

0 引言

针对约束空间内爆炸问题，爆炸后燃烧效应是需要重点关注的内爆炸物理现象。大多数炸药（例如TNT、温压炸药、SDF（Shock-Dispered-Fuel）混合型炸药［1］等）的爆轰产物具有负氧性，在膨胀的过程中会与周围空气中氧气发生剧烈的燃烧反应，释放出大量能量，形成爆炸后燃烧效应［2］。当爆炸发生在约束空间内时，因壁面限制，相比空爆会进一步加剧后燃烧效应，从而对冲击波的壁面反射压力、准静态压力等产生一定的增强效应。

迄今，针对约束空间内后燃烧效应对爆炸载荷的影响规律，国内外学者开展了大量的实验和数值模拟研究。国内的相关研究主要集中在西安近代化学所和西北核技术研究所。例如，姬建荣等［3］在小型爆炸容器内，实验测量了在密闭和半密闭爆炸工况下TNT-AL炸药的后燃烧性能，结果表明当铝粉质量分数为20%时，TNT-AL炸药在小型爆炸容器中较易发生后燃烧反应。研究人员用高速摄影仪观测到了后燃烧反应及其发展过程，发现后燃烧反应在爆炸腔内形成了一定的准静态压力，持续时间达数十毫秒。钟巍和田宙［4-5］基于理想气体状态方程和能量守恒定律，将准静态压力划分为爆炸压力（等熵假设/等压假设）和化学反应压力2个部分进行计算，推导了考虑爆炸产物发生化学反应后在密闭空间内的准静态压力计算公式；金朋刚等［6］在密闭容器内通过实验测量了含有3种粒度（0，13，130 μm）的铝粉HMX基炸药的准静态压力，结果表明，铝粉可以提高HMX基炸药在密闭空间爆炸的准静态压力，小颗粒铝粉相比大颗粒铝粉更有利于提高准静态压力。在国外，美国劳伦斯·利弗莫尔国家重点实验室的 Kuhl等［1，7-11］采用自主开发的三维自适应网格加密程序（AMR3D），数值模拟了1.5 g SDF炸药在不同容积柱形、矩形密闭容器内的爆炸过程。该程序采用两相模型构建SDF炸药模型，即将PETN或TNT炸药爆轰产物视为连续介质气相进行模拟，将片状铝粉视为连续介质固相进行模拟，气相和固相间通过简化经验模型来描述质量、动量及能量的转换。Balakrishnan等［12-14］提出了气相和固相耦合的数值计算模型，研究了开敞环境下TNT-AL炸药爆炸产物的界面失稳及其与铝粒子相互作用的过程，并考虑了铝粒子与多组分爆轰产物的后燃烧反应，其中气相被视为连续介质来处理，固相被视为离散介质并采用拉格朗日方法来捕捉。为近似描述内爆炸的后燃烧效应，徐维铮等［15］提出了一种应用于内爆炸数值计算的简化反应率模型，探讨了模型中能量释放常数及后燃烧能量释放大小对爆炸超压载荷的影响规律。然而，该反应率模型中能量释放常数需根据实际的内爆炸过程来确定，而文献［15］中尚未给出具体的确定方法。为此，本文将提出一种近似预估反应率时间历程的理论公式，在此基础上进一步根据内爆炸化学反应的时间确定能量释放常数。

1 控制方程及数值求解

爆炸后燃烧涉及爆轰产物与周围空气复杂的多组分化学反应过程，若详细考虑各组分的反应流动，不仅程序编写复杂，且网格尺寸需设置得很密，计算时间也很长，这些缺点均不便于在实际工程中快速计算。为近似考虑爆炸的后燃烧效应，文献［15］中提出了一种简化反应率模型，即

式中：a为能量释放常数；α为内爆炸后燃烧反应率（初始时α=1，反应完成后α=0）；p为气体压力；l，n分别为反应率指数和压力指数，l=1 2，n=1/6［16］。

将上述反应率模型耦合到二维可压缩欧拉方程，即

其中，

式中：U为守恒变量；F，G分别为 x，y方向上的数值通量；S为能量源项；ρ为气体密度；u，v分别为 x，y方向上的速度分量；E为单位体积气体的总能量；e为气体内能；Qaf为爆炸后燃烧过程中单位质量释放能量；γ为气体绝热指数，本文中γ=1.4。

本文依次采用五阶WENO格式和三阶TVD龙格—库塔（TVD-RK）法对上述方程中的对流项和时间项分别进行数值重构及数值离散［17］。

2 内爆炸后燃烧反应率数值计算

本节将采用自主开发的程序对约束空间内爆炸后燃烧反应率的时间历程进行数值计算，主要探讨能量加入对反应率的时间历程的影响规律。

2.1 舱室尺寸及测点布置

计算舱室为长方形，具体尺寸如图1（a）所示。在炸药中心处设置了4个典型测点来监测爆炸载荷及反应率的时间历程。均匀网格步长取为10 mm，如图1（b）所示。

图1 舱室尺寸及网格划分Fig.1 Sizes of cabin and mesh division

2.2 初始条件和边界条件

基于瞬时爆轰假定［18］，将方形炸药等效为均匀的高压气团，具体参数如下：边长44.4 mm，密度 1 630 kg/m3，压力 3.057 9×109Pa。炸药设置在舱室中间，周围区域为空气域，空气密度为1.0 kg/m3，压力为1.0×105Pa。初始时刻反应率分布如下：在炸药所在区域，α=1；在舱室其他区域，α=0。壁面边界条件设置为刚性边界。由于冲击波与结构变形耦合效应十分复杂，这里暂时不考虑舱室结构的变形。

2.3 计算工况

为了探讨能量释放常数a和后燃烧过程中单位质量释放能量Qaf对反应率时间历程的影响规律，本文选取了2种典型工况进行计算。这里没有针对具体的实际爆炸工况，而是任意选取系列参数。对于工况1，Qaf=4.69×106J/kg，并保持其他参数不变，取4种不同的能量释放常数（a=10，20，30，40）。对于工况 2，a=10，并保持其他参数不变，取4种爆炸后燃烧过程单位质量释放能量（Qaf=1.0×106，2.0×106，3.0×106，4.69×106J/kg）。

2.4 能量加入对反应率时间历程的影响

图2（a）和图2（b）分别给出了工况1和工况2下测点4处反应率的时间历程曲线。

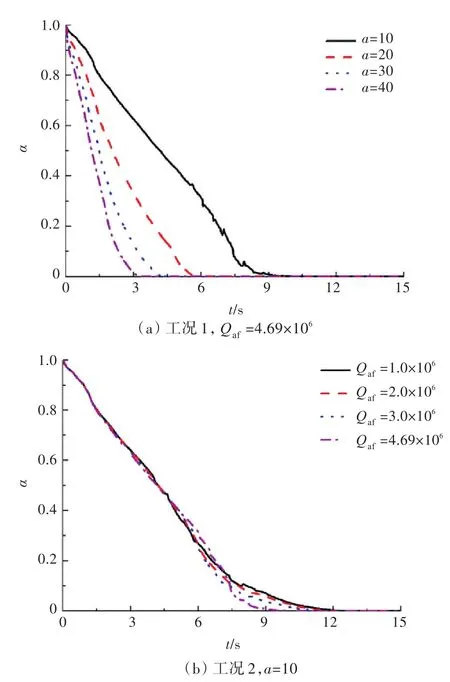
图2 不同工况下测点4处的反应率时间历程曲线Fig.2 Time history curves of reaction rate at gauging point-4 for different cases

由图2（a）可看出，在后燃烧能量Qaf一定时，能量释放常数a对反应率时间历程曲线的影响显著，反应率衰减速度随着a的增大而增大。

由图2（b）可看出，当能量释放常数a一定时，Qaf对反应率时间历程的影响较小，在爆炸初期，各反应率时间历程曲线基本重合，仅在爆炸后期存在一定的差异，且随着Qaf的增大，反应率衰减速度加快。

3 反应率时间历程理论预估

由2.4节的算例可知，后燃烧能量的加入对反应率时间历程具有一定的影响规律，那么能否采用简化理论对上述影响规律进行阐释和预估？为了对炸药中心处测点4的反应率时间历程曲线进行理论预估，对式（1）进行变量分离，得

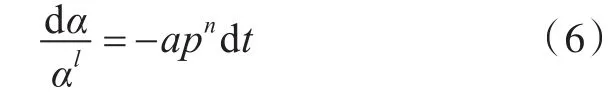
由于气体压力 p在内爆炸过程中随着时间的变化而变得非常复杂，为了近似预估反应率的时间历程，并考虑到密闭空间内爆炸载荷中准静态压力占主要成分，得到如图3所示结果。

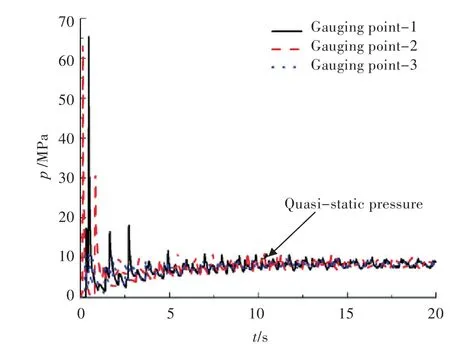
图3 密闭舱室内爆炸超压载荷时间历程曲线（a=10，Qaf=4.69×106）Fig.3 Overpressure time history curves of explosion in closed cabin（a=10，Qaf=4.69×106）

这里选取准静态压力峰值 pQS代替 p对式（6）进行积分，可得

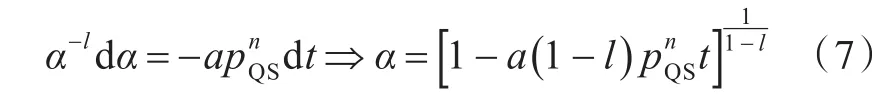
若令式（7）中的α=0，可得反应结束时刻tf：

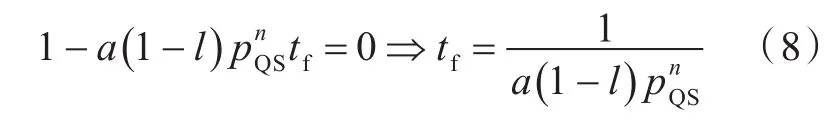
其中，pQS的计算公式为［19］

式中：m为炸药质量；V为舱室体积；Qtol=QTNT+Qaf，为爆炸过程中释放的总能量，其中 QTNT为炸药爆热，QTNT=4.69×106J/kg；p0为初始大气压力；ρE为炸药密度，ρE=1 630 kg/m3。

由式（7）～式（9）得到密闭空间内爆炸炸药中心处测点4的反应率时间历程理论预估公式。主要计算流程如下：对某爆炸工况，首先根据式（9）计算 pQS，然后根据式（8）计算反应结束时刻tf，最后，根据式（7）得到反应率的理论时间历程。

为了验证理论预估公式的可靠性，对工况1和工况2炸药中心处测点4的内爆炸后燃烧反应率进行数值计算，得到了如图4和图5所示时间历程曲线的数值与理论计算对比结果。由图4和图5可知，虽然在爆炸初期和爆炸后期理论值与数值计算结果存在一定的差异（pQS代替 p造成的），但总体趋势吻合较好。

图4 工况1测点4的反应率时间历程曲线数值与理论值对比Fig.4 Comparisons of reaction rate time history curves at gauging point-4 between numerical and theoretical results in explosion case 1

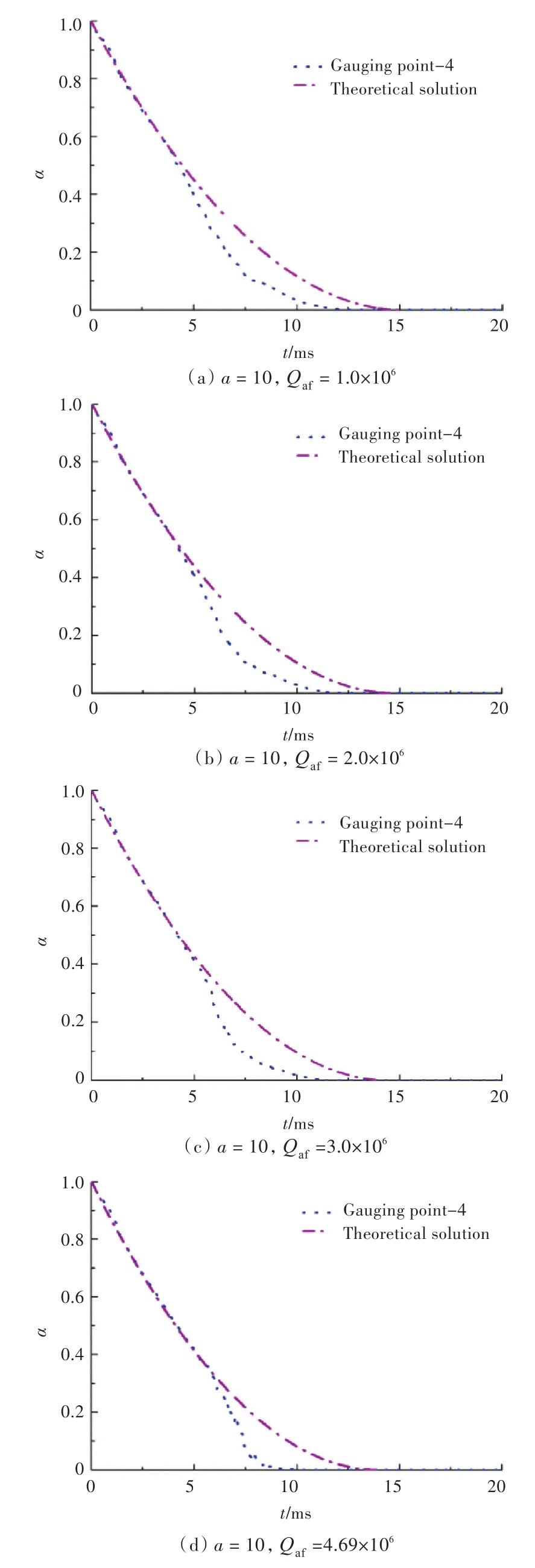
图5 工况2测点4的反应率时间历程曲线数值与理论值对比Fig.5 Comparisons of reaction rate time history curves at gauging point-4 between numerical and theoretical results in explosion case 2

4 能量释放常数的确定

在2.3节计算工况中，能量释放常数a是任意选取的，然而若要模拟真实爆炸过程中的后燃烧效应，还需确定简化反应率模型中的a值。本节给出一种近似确定方法。根据式（8），可进一步得到a的表达式为

由式（10）可知，若可以近似预估密闭舱室内爆炸的化学反应结束时刻tf，则可确定a值。文献［20］中给出了基于化学反应动力学确定tf的方法。这里以TNT炸药舱室内爆炸为例，简要说明确定tf的方法。

TNT炸药爆炸的化学反应式为

根据式（11）及舱室内爆炸时TNT的质量m和摩尔质量MTNT，可得到如下爆轰产物中各组分的浓度：

式中，c为组分浓度，mol/m3。

排除炸药占据的体积，可得周围空气所占体积VKQ为

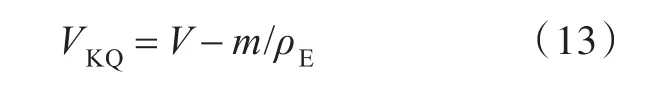
根据舱室内VKQ及对 N2，O2这2种组分体积分数（79%，21%）的基本假定，可得到空气中各组分浓度为

式中，Vmol为气体的摩尔体积，Vmol=0.024 m3/L。

文献［20］中给出的典型算例：药量体积比m/V=0.6 kg/m3、炸药密度 ρE=1 640 kg/m3。根据式（12）和式（14）的计算，可得舱室内各组分的初始时刻浓度如下：

根据舱室内药量体积比对化学反应的划分［4］，可知在此爆炸算例下（m/V=0.6 kg/m3），舱室内将依次发生如下3种化学反应：

针对式（15）的化学反应1，其反应速率常数k=0.072 6（mol·m-3）-2/ms。这里，反应速率常数根据Arrhenius定理k=Ae-Ea/RT（其中Ea为活化能，R为理想气体常数，R=8.314（J·mol-1）/K，T为热力学温度，A为指数前因子）计算得到。

进一步，可列出各组分化学动力学控制方程为

其中，各组分浓度初始条件的计算结果为：

通过采用龙格—库塔法进行数值求解，得到如图6所示结果。由图6可知，该反应结束时刻tf近似为15 ms。

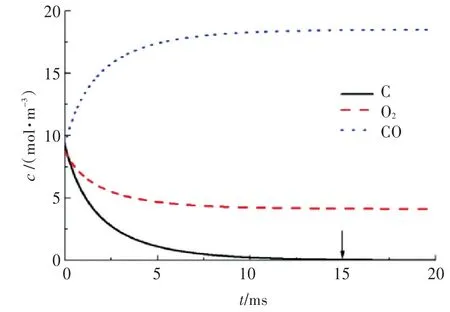
图6 反应1（式（15））各组分浓度随时间变化曲线Fig.6 Concentration of each component time history curves for reaction one（Eq.（15））

同理，针对式（16）的化学反应2，将其划分为两步反应进行计算。

式中，反应速率常数 k1=0.021 4（mol·m-3）-2/ms，k2=0.022 4（mol·m-3）-2/ms。

进一步，可列出各组分化学动力学控制方程为

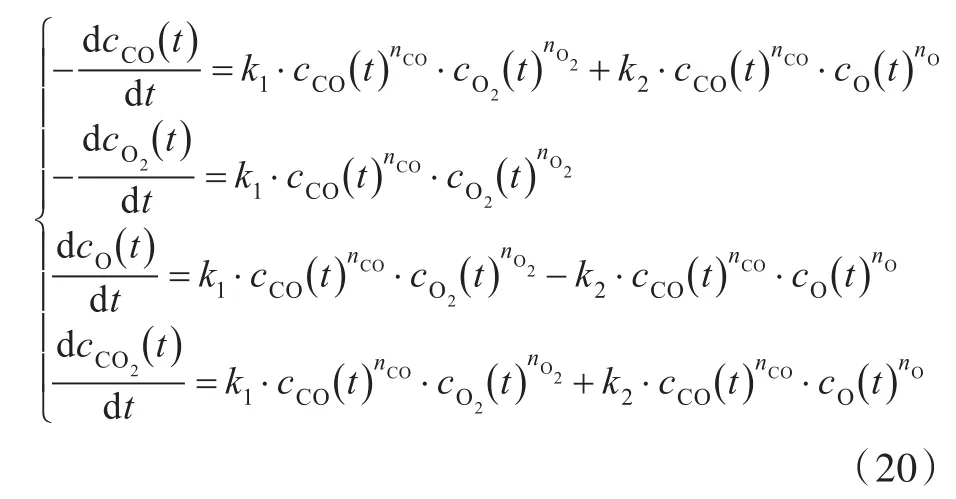
式中，nCO，nO2，nO分别为组分CO，O2，O所对应的化学反应级数。其中，各组分的化学反应级数为

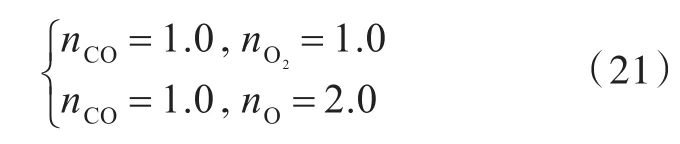
根据式（18），反应后各组分浓度初始条件的计算结果为：

通过采用龙格—库塔法进行数值求解，得到如图7所示结果。由图7可知，该反应结束时刻tf近似为15 ms。

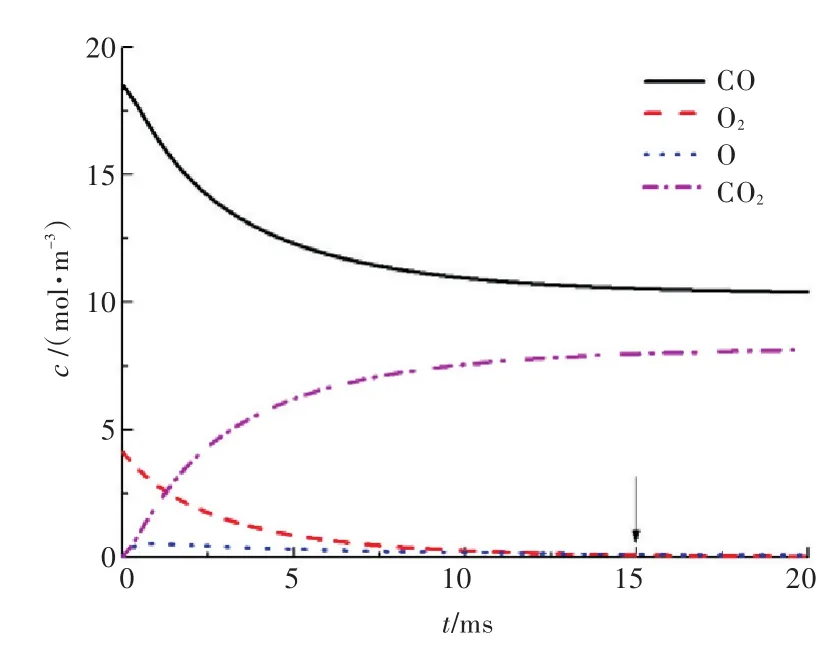
图7 反应2（式（16））各组分浓度随时间变化曲线Fig.7 Concentration of each component time history curves for reaction two（Eq.（16））

同理，针对式（17）的化学反应3，其反应速率常数 k=0.222 4（mol·m-3）-2/ms，进一步可列出各组分化学动力学控制方程为

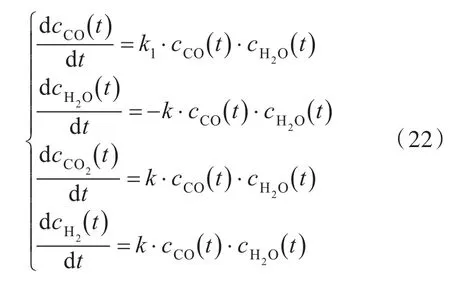
根据式（20），反应后各组分浓度初始条件的计算结果为：

通过采用龙格—库塔法进行数值求解，得到如图8所示结果。由图8可知，该反应结束时刻tf近似为5.0 ms。

图8 反应3（式（17））各组分浓度随时间变化曲线Fig.8 Concentration of each component time history curves for reaction three（Eq.（17））

由于以上3种反应在真实的内爆炸过程中不一定严格按照上述反应顺序进行（可能各个反应同时在进行中），作为对内爆炸时间尺度的一种估算，将以上3种反应时刻的平均值作为总的化学反应结束时刻。由上述结果可知，在m/V=0.6 kg/m3药量体积比工况下，tf≈11.7 ms。文献［20］针对此工况下的TNT内爆炸开展了实验测量研究，实验测量的准静态超压曲线如图9所示。

图9 在m/V=0.6 kg/m3下反应3的准静态超压时间曲线［20］Fig.9 Quasi-static overpressure time history curves of reaction three at m/V=0.6 kg/m3［20］

由图9可知，在爆炸初期冲击波壁面反射形成多峰值载荷特征；在爆炸中期，爆炸产物与舱室内部气体充分混合后开始发生剧烈的化学反应并释放能量，导致准静态压力回升；在爆炸后期，化学反应逐渐完成，准静态压力也趋于稳定。此外，化学反应起主要作用的时间段约为10 ms，这也初步说明了按照上述化学反应动力学分析方法近似确定的化学反应结束时刻tf具有一定的合理性和可靠性。

这里需要注意的是，由于确定化学反应时间具有一定的难度，它涉及详细的化学反应分析及其与爆炸流场的耦合；同时，实验手段并不能直接测量得到化学反应的时间历程，只能通过可测物理量（例如，压力和温度）等数据进行反推或估算；用上述基于简化的化学反应分析来近似预估化学反应时间，仍需要更多的内爆炸实验数据进行系列验证及分析。

5 结 论

通过本文的研究，得到如下主要结论：

1）当内爆炸后燃烧能量大小一定时，能量释放常数a对反应率时间历程曲线的影响显著，反应率衰减速度随着a的增大而增大。在a一定时，后燃烧能量大小对反应率时间历程的影响较小，在爆炸初期，各反应率时间历程曲线基本重合，仅在爆炸后期存在一定的差异。

2）所提的用于近似预估反应率时间历程的理论公式具有一定的可靠性，作为一种近似方法，在数值计算前可近似预估反应率时间历程。

3）根据化学反应动力学分析方法，近似确定化学反应结束时刻tf具有一定的合理性和可靠性，按照反应率理论预估公式，可进一步确定反应率模型中的能量释放常数a，这可为模拟真实的内爆炸后燃烧效应提供一定的参考和指导。