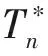不同协方差下高维数据的MANOVA检验问题

李顺勇,王一静

(山西大学 数学科学学院,山西 太原 030006)

0 引言

本文就高维数据下总体均值假设检验问题寻求更好的检验统计量,做了进一步的工作。下面首先介绍高维数据下多样本的总体均值假设检验问题:

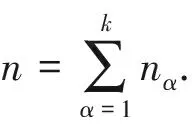
H0:μ1=μ2=…=μkVSH1:H0不成立。

(1)

该假设问题也称为多变量k样本Behrens-Fisher问题或MANOVA检验问题。

近十几年来,基于上述假设检验问题,许多学者进行了大量的研究,其中Zhang等[2]及Xu等[3]分别在2009年和2015年都给出了k-样本Behrens-Fisher问题的近似解;Srivastava等[4]于2006年在多元线性回归模型下提出了一个标度不变量的GLHT检验方法;2012年,Yamada等[5]研究了在高维线性回归中的GLHT假设检验问题;Srivastava等[6]在2013年针对非正态数据推广了Yamada的检验方法;2015年,Yamada等[7]提出了一种不需要假设共同协方差阵的MANOVA检验方法。但当样本协方差不同时,应用上述方法可能会出现错误的结果。为了解决这个问题,曹明响等[8]于2015年在Chen的思想上进行扩展从而提出了一个新的检验统计量;2017年,Zhou等[9]基于C-Q[10]和Feng等[11]的理论并利用 U统计量[12]也得到一个新检验统计量。

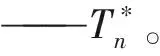
1 新检验统计量及其渐近分布

1.1 构建检验统计量

本文构造的新检验统计量是基于Chen等[13]的思想提出来的,实现了数据从两样本到多样本的提升。记

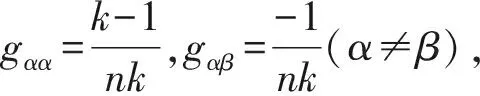
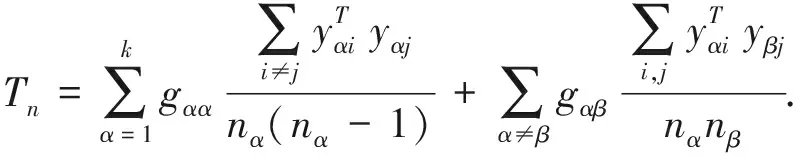
(2)

本文基于Tn提出了一个新的检验统计量:

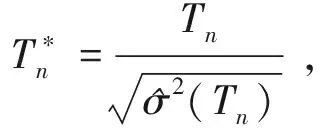
(3)

其中,

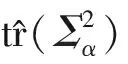
式(2)经过线性运算,可以得到(4)和(5)两种Tn表达式:

式中,

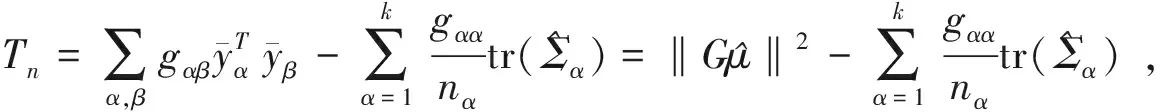
(4)

为了更好说明Tn的方差,令xαi=yαi-μα,i=1,2,…,nα,α=1,2,…,k.对于每一个α=1,2,…,k,xα1,xα2,…,xαnα是独立同分布的,并且满足Ε(xα1)=0,cov(xα1)=Σα.故Tn又可写成下式:

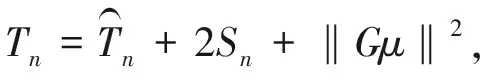
(5)

式中,

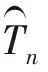
由此得出了在原假设下Tn的方差:

1.2 新检验统计量的渐近性

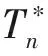
yαi=μα+Λαzαi,i=1,2,…,nα,α=1,2,…,k，

(6)

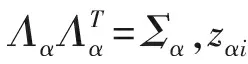
xαi=Λαzαi,i=1,2,…,nα,α=1,2,…,k.

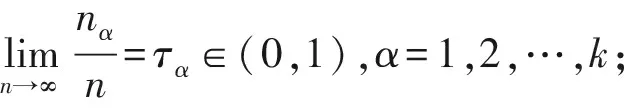
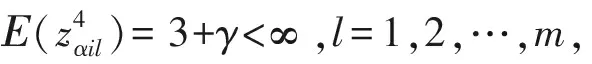
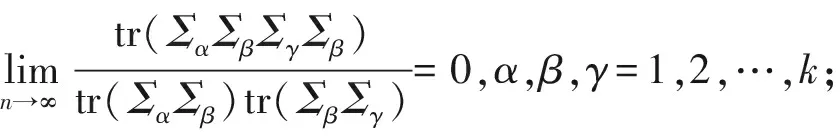
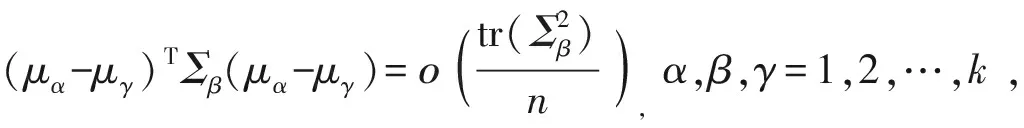
其中Ⅳ是高维检验问题中经常使用的一个表达式,它衡量了不同总体间均值的差异性。

其中,

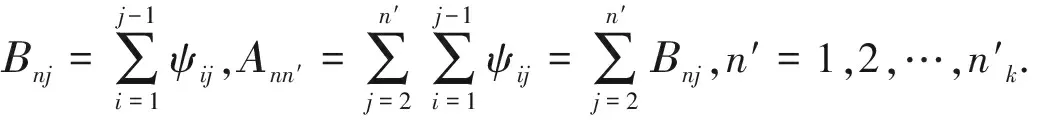
引理2[9]在假设条件Ⅰ-Ⅲ下,有

其中gαβ和gβγ是矩阵G中的元素。再根据假设Ⅳ得到:

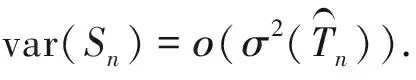
(7)

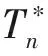
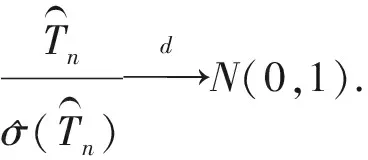
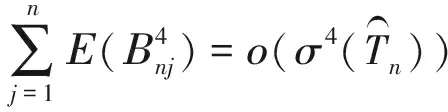
进而可以得到林德伯格条件:

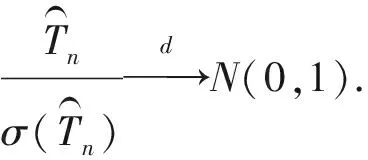
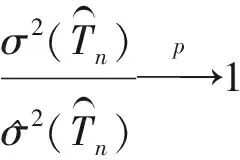
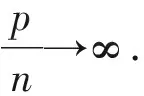
定理2在同定理1一样的假设条件以及模型(6)和式(7)下,当n,p→∞可以得到:

其中zα和Φ(·)分别表示标准正态分布的上侧α分位数和累积分布函数。

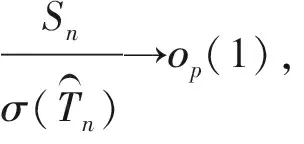
再根据(5)有

2 数值模拟

对于高维MANOVA问题(1),Zhou等[9]提出的TZ可以重新表示为:

TY-H是Yamada和Himeno在2015年提出的检验统计量,则标准化后的统计量为:

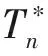
表1 检验水平(百分比)

表2 检验功效(百分比)

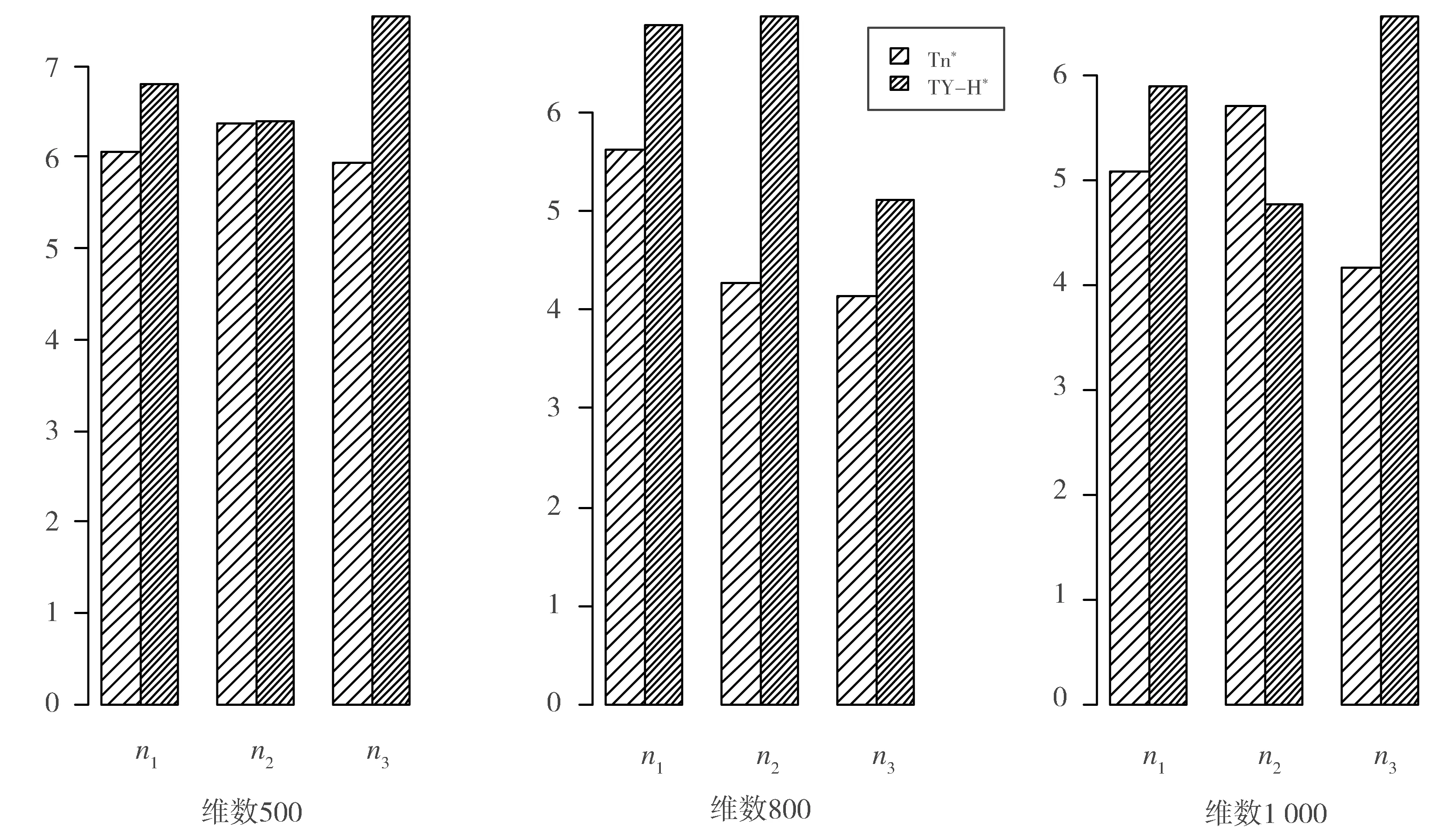
Fig.1 Comparison of test levels between 图 与的检验水平对比图

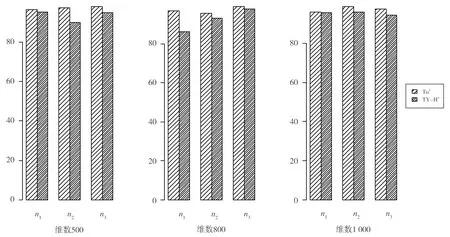
Fig.2 Comparison of test efficiency between 图 与的检验功效对比图

3 结论