基于进化粒子群算法的军事训练计划智能优化

杜尚华,樊率军,赵玉建

(国防大学联合作战学院,河北石家庄 050000)

军事训练中的补差训练计划生成与优化是基层部队日常组训的难点,其核心问题在于解决对薄弱训练课目、组训者和参训人员的最优化分配,以保证在有效时间内最大限度利用训练场地和装备器材资源,达成训练效益最大化,提升官兵整体训练水平。补差训练计划优化问题可看做是经典排课问题的延伸,其在20世纪70年代已被证明属于NP完全问题[1]。随着计算机运算能力的日益提升,众多智能优化算法被设计提出,为补差训练计划优化问题提供了技术可行解法。智能优化算法的发展可分为经典公式阶段和实践应用阶段,前期的优化算法主要有拉格朗日松弛法[2]、切割平面法[3]、整数规划法[4]等,其原理是通过公式演算找到局部极值,用以模拟全局最优值,算法约束条件较为苛刻,必须具备线性连续、可微等函数特点;应用阶段的优化算法则通过模拟生物种群习性设计算法框架,代表性的优化算法有遗传算法[5]、蜂群算法[6]、蚁群算法[7]、蛙跳算法[8]、萤火虫算法[9]、鱼群算法[10]、粒子群算法[11]等,其原理是通过伪随机变量模拟生物某项生理特征,通过多代演化使局部最优解逼近全局最优解。此类算法突破了线性约束条件限制,为工程应用奠定了技术基础,但也普遍存在收敛效率低、收敛时间不确定、易于陷入局部最优陷阱等问题。本文在总结前人研究基础上,通过对比分析粒子群算法和遗传算法的异同,提出融合了生物进化特征的进化粒子群算法,并将其应用于补差训练计划优化工程实践中,实现了训练计划的自动生成和智能优化。

1 问题描述

补差训练计划智能优化问题可划归排课问题,但又有其独立特征,区别主要在于:1)组训者只在前日制定当天的补差训练计划,而排课通常为未来数日课程进行统一编排;2)补差训练课目和组训者由组训者手工输入,而排课通常由规则限制自动生成课目和授课人;3)补差训练计划以参训人员历史成绩作为优化依据,而排课通常以参训人员选课情况作为优化依据。基于此,补差训练计划优化问题描述如:算法输入为组训者手工选定当日的训练课目、训练时间段、组训者。设组训课目集合为K,训练时间段集合为T,参训人员集合为R。定义补差训练计划的评估指标如下:

1)平均分:用以衡量训练计划下所有参训人员在该训练课目此前1个月内的平均成绩,记为T1。

2)参训率:用以衡量训练计划下所有参训人员在该训练课目此前1个月内参加训练天数占该课目训练总天数的比例,记为T2。

3)优秀率:用以衡量训练计划下所有参训人员在该训练课目的成绩达到优秀成绩的比例,记为T3。

4)训练强度:用以衡量训练计划下所有参训人员在训练当日的累计疲劳程度,参训课目越多越疲劳,则训练强度指标越大,记为T4。

5)同班率:用以衡量训练计划下每个训练课目的参训人员来自相同班级的程度,班级越多人员越零散,则同班率指标越低,记为T5。

设补差训练计划的综合评分为F,则建立数学模型如下

(1)

模型描述为:在(K,T)输入限制条件下,合理调整R范围,使T1-4取得最小值,T5取得最大值,并使综合评分F(K,T,R)达到全局最大值。考虑到补差训练计划的工程应用性,还应引入如下硬约束条件:

1)训练时间段有冲突的组训课目内不得有重复人员出现。

2)同一组训课目内不得有重复人员出现。

3)从未参加过某课目训练的人员记为不参训该课目。

2 算法构建

根据问题描述,算法要实现当日训练课目、训练时间段、组训者的手工输入,通过进化粒子群算法实现参训人员的智能优化。即要设计3个子算法:1)课目、组训者排序算法;2)训练计划综合评分算法;3)智能优化算法。算法流程如图1所示。

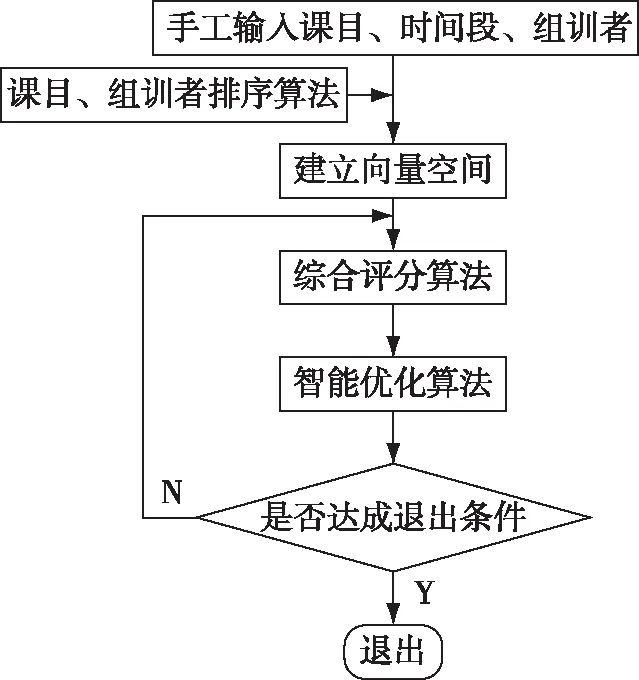
图1 补差训练计划优化算法流程图

2.1 课目、组训者排序算法

该算法计算目的在于为组训者提供手工输入量化排序结果,便于找到训练薄弱课目和与该课目对应的最高成绩所在班班长(组训者默认从各班班长中优选)。课目排序参照指标为此前1个月该参训课目的平均优秀率,组训者排序参照指标为此前1个月各班人员在该参训课目的平均分。设此前1个月内共有m个课目参训,参训人员总数为n,其中第i个人在第j个训练课目的平均成绩为fij,则其优秀率yij计算公式为

(2)

课目j的优秀率Yj计算公式为

(3)

设第k个班级内共有r个人,则该班平均分Pkj计算公式为

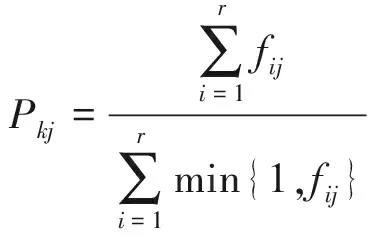
(4)

2.2 综合评分算法

本文设计使用熵权法和理想点法融合的熵权理想点方法作为多指标融合评分算法,将补差训练计划的平均分、参训率、优秀率、训练强度、同班率指标合并为综合评分结果代入智能优化。

2.2.1 评估指标计算

某项补差训练计划中,设同班率为T,平均分为F,优秀率为Y,训练强度为Q,参训率为C;共安排了p个训练课目,其中第j个补差班级内的人员数为nj;此前1个月内,课目j共组织考核m次,其中人员i的该课目平均分为fij,则优秀率yij计算公式同公式(2),参训率cij的计算公式如下

(5)

设人员i在补差训练中共参与训练xi次,则人员i的训练强度qi计算公式为

qi=exi-xi

(6)

则补差训练计划的各评估指标计算公式为：

(7)

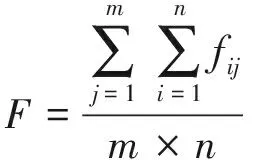
(8)

(9)

(10)

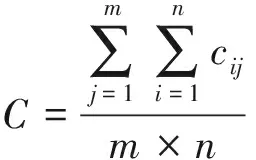
(11)

2.2.2 多指标融合计算

熵权法借鉴了自然界熵的概念,引入熵权重作为各评估指标的权重,使个体区分度大的评估指标获取更大权重[12]。设平均分、参训率、优秀率、训练强度、同班率分别对应T1至T5评估指标,共有n个补差训练计划参与综合评分计算,则构建出评估指标矩阵X,对应的子项xij表示第i个计划中的第j项评估指标值。熵权重计算步骤如下:

1)归一化处理矩阵X,生成归一化矩阵P。

(12)

2)计算熵值ej。

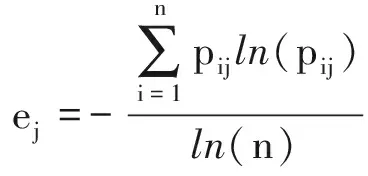
(13)

式中,若pij=0,则ej=0。

3)计算熵权重tj。

(14)

理想点法构思利用评估指标建立多维空间,每个参评对象映射为多维空间中的向量,将最优的评估指标值汇总生成正理想点位,最差评估指标值汇总生成负理想点位,通过计算每个参评对象和正负理想点位之间的距离,获取综合评分[13]。融合熵权重的熵权理想点法计算步骤如下:

1)生成正负理想点位A+和A-。设归一化矩阵P值为pij,则最优评估指标值pj+和最差评估指标值pj-计算公式为:

(15)

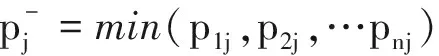
(16)

2)计算第i个补差训练计划距离A+和A-的距离d+和d-。考虑到各评估指标区分度差异,将熵权重tj代入,熵权理想点法计算公式为:

(17)

(18)

3)计算各补差训练计划的综合评分Mi。计算公式为

(19)

2.3 粒子群算法

粒子群算法由Kennedy和Eberhart在1995年提出,借鉴生物界中鸟群的觅食行为,算法建立多维空间,向空间释放多个随机个体,将综合评分结果看作食物,则参评个体会根据空间中各位置的综合评分高低自发向食物丰沛区游走,并在多代游走后找到全局最优位置[14]。具体算法如下:

Step1:建立D维空间,设补差训练计划共参训m个课目,第j个课目参训人数为nj,则D的维度计算公式如下

(20)

Step2:设置初始种群。设种群中包含1 000个个体,个体内部存储当前位置和历史最优位置及其对应分值，其结构体如表1所示。

表1 粒子群个体结构表

Step3:计算每个个体下一步的游走位置。设个体当前位置为Xi,Pi为个体第i次游走遍历到的最优位置,Qi为种群经过i次游走的最优位置,Vi为个体第i次游走的步长;r1和r2为[0,1]之间的随机实数。则个体第i+1次游走的步长Vi+1计算公式为

Vi+1=0.5Vi+0.3r1(Pi-Xi)+0.3r2(Qi-Xi)

(21)

个体的第i+1次游走位置Xi+1计算公式为

Xi+1=Xi+Vi+1

(22)

Step4:调用熵权理想点法计算该位置的综合评分。

Step5:使用冒泡法更新个体的历史最优评分位和种群的当前最优综合评分位。

Step6:重复Step3-Step5。并判断是否满足退出条件:种群最优评分的多代差值到达收敛阈值。满足退出条件则退出算法,输出种群最优位置及其对应综合评分。其算法流程如图2所示。

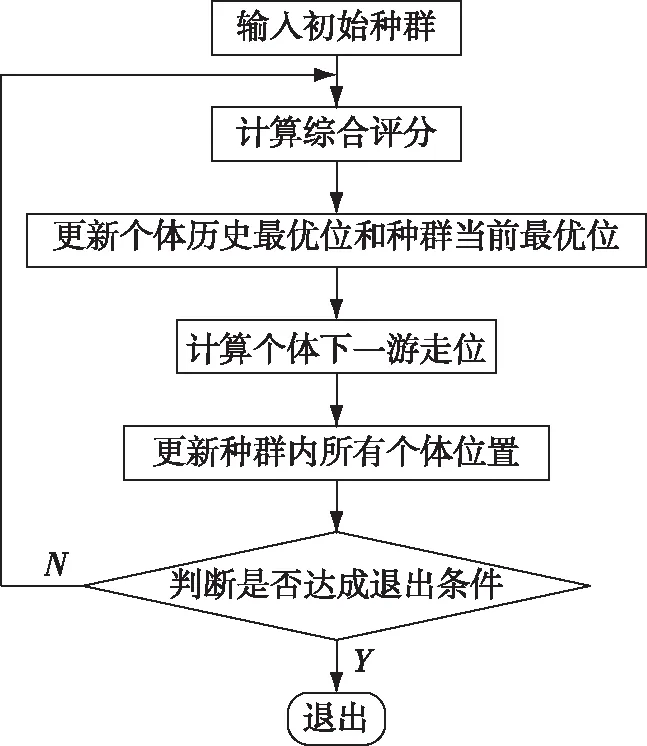
图2 标准粒子群算法流程图

2.4 量子粒子群算法

粒子群算法虽然在多代游走后能够使最优位置趋向于全局最优,但也易于陷入局部最优陷阱,为解决上述问题,Sun等人提出量子粒子群算法,将量子迁移思想引入个体位置计算中,使个体具备全空间迁移能力,一定程度上解决了全局寻优问题[15]。与标准算法相比,量子粒子群算法的步长Vi+1计算公式为

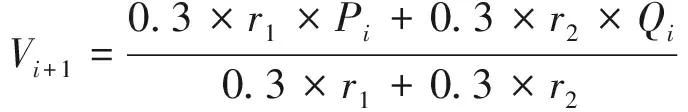
(23)

设种群内个体数目为n,Pij表示种群内第j个个体在第i次游走后的历史最优位。引入第i次游走的迁移系数Mi计算公式为

(24)

设u为[0,1]之间的随机实数。位置Xi+1计算公式为

(25)

算法其余部分同标准粒子群算法。

2.5 遗传算法

遗传算法借鉴自然界物种优胜劣汰的进化机制,通过构建生物种群,模拟出生物的繁殖、变异、适应和淘汰进程,通过多代进化使后代个体具备更强的适应度,取得更高的综合评分[16]。具体算法如下:

Step1:设置初始种群。种群中包含随机产生的1000个个体。

Step2:计算1 000个体的综合评分。

Step3:个体淘汰。首先删除寿命超过上限的个体,其次依据“高分个体淘汰概率小,低分个体淘汰概率大”的原则使用轮盘法优选个体,最终优选出100个个体。

Step4:种群繁殖变异。使用轮盘法挑选出高分个体作为父代个体,然后以千分之一的概率使其参训人员发生变异,产生与父代个体相似的子代个体,最终使种群规模达到1 000。

Step5:重复Step2-Step4。并判断是否满足退出条件:种群最优个体综合评分是否收敛。满足退出条件则退出算法,输出最优个体及其对应综合评分。

通过上述算法分析可以发现,粒子群算法和遗传算法作为智能优化算法具有较多相似点,如建立初始种群、设置随机变量、随机变异游走、以局部最优收敛至全局最优等。区别主要在于:1)遗传算法可以在最优个体的基础上不断回溯变异,粒子群算法作为随机游走算法无法回溯,这就造成了粒子群算法较遗传算法更容易陷入局部最优陷阱;2)遗传算法的变异是随机行为,粒子群算法的变异受个体最优和全局最优解的制约,使随机行为可控,这就造成了遗传算法收敛效率相比粒子群算法更低。

2.6 进化粒子群算法

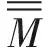
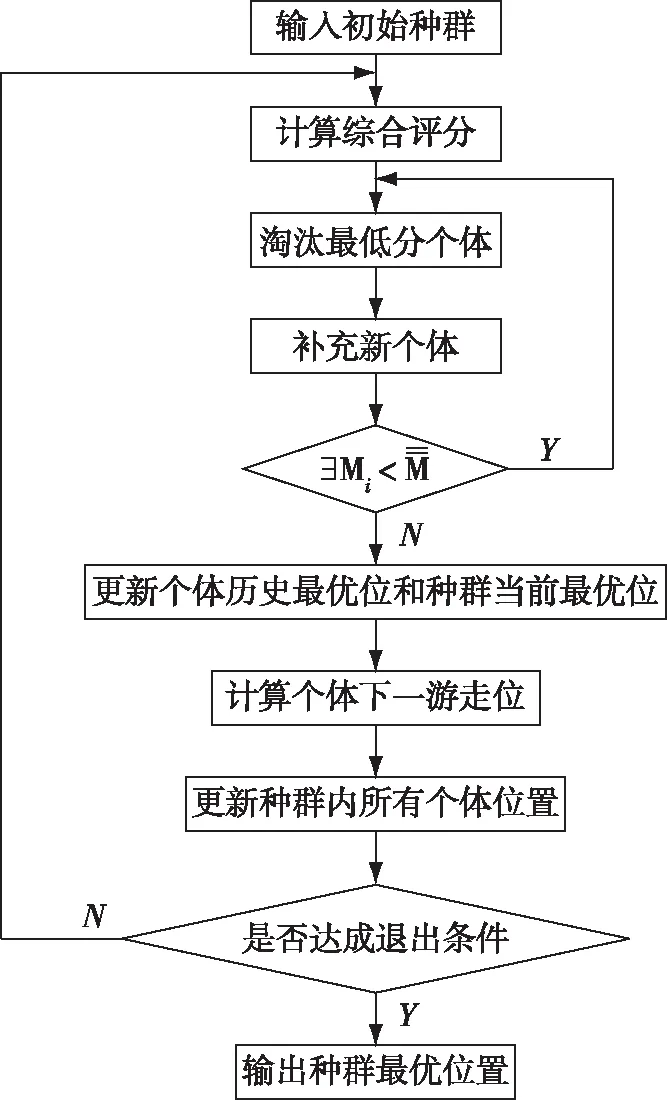
图3 进化粒子群算法流程图

具体算法如下:

Step1-Step4:同量子粒子群算法。

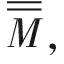
Step6:补充新个体。使用轮盘法挑选出高分个体的历史最高分值位置,在此位置产生子代个体,最终使种群规模达到1 000。

Step7:更新个体和种群的最优评分位置。

Step8:重复Step3-Step7。并判断是否满足退出条件:种群最优位置评分值是否收敛。满足退出条件则退出算法,输出种群最优位置及其对应综合评分。

3 仿真实验

为了检验遗传算法、粒子群算法、量子粒子群算法、进化粒子群算法等4种智能优化算法在补差训练计划智能优化中的性能,本文依托工程实例项目设计开发“军事训练分析系统”中的“补差训练模块”,模块整体界面如图4所示。

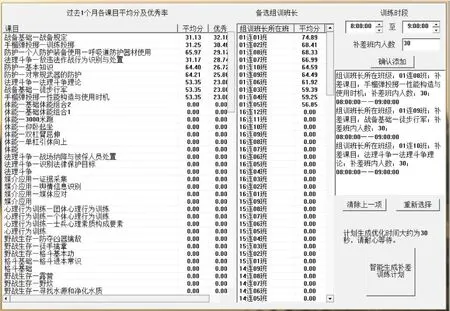
图4 补差训练智能优化模块整体界面

计算机配置:Intel酷睿双核T7300 2.0 GHz中央处理器;3 G内存;32位Win7操作系统;vc6.0系统开发环境。

3.1 各智能优化算法收敛性比较

实验设计使用统一的补差训练计划评估指标(平均分、参训率、训练强度、优秀率、同班率)和综合评分算法(熵权理想点法),演化相同代数(650代),各智能优化算法的各代最优个体综合评分结果如图5所示。

图5 各智能优化算法各代综合评分结果

实验结果表明:在进化相同代数时,遗传算法综合评分效果最差,量子粒子群法和本文设计的进化量子粒子群法效果最好,标准粒子群法效果居中;相比较而言,本文设计的进化量子粒子群法能够利用淘汰和繁殖时机达成个体分值的突变陡增,使群体综合评分整体上升,该特性也存在于遗传算法的统计图中,标准粒子群法和量子粒子群法不具备此特性。

3.2 各智能优化算法结果比较

分析各智能优化算法达成综合评分收敛的代数统计情况,对比分析如表2所示。

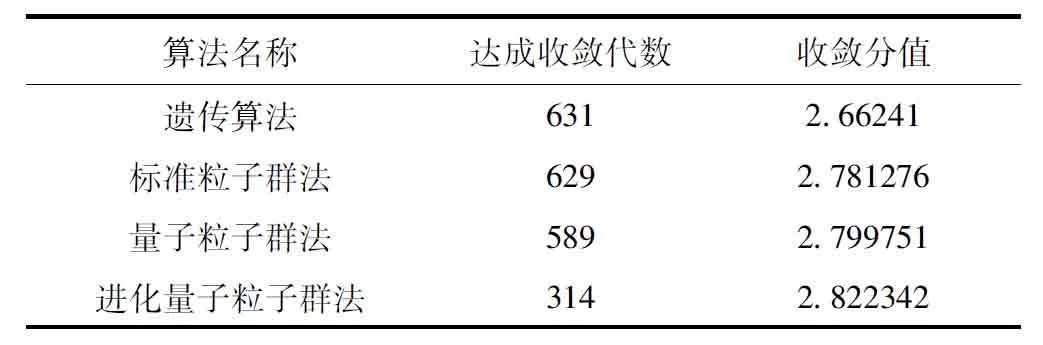
表2 各智能优化算法收敛代数统计表

实验结果表明:相比较而言,进化量子粒子群法在收敛代数和收敛分值上均要优于主流智能优化算法。

3.3 各智能优化算法效率比较

在进化相同代数时,分别选取2-10个训练课目,分析各智能优化算法的计算耗时如图6所示。

实验结果表明:遗传算法的计算耗时最短,进化量子粒子群法的计算耗时最长,10课目时的耗时差异为14.75 s。相比于传统的手工拟制补差训练计划,各智能优化算法的计算耗时都在可容忍范围内。

3.4 补差训练计划结果分析

通过上述实验分析,本文设计的进化量子粒子群法综合性能较其他对比智能优化算法优化效果更显著,将该算法代入补差训练计划智能优化模块,得到补差训练计划如表3所示。

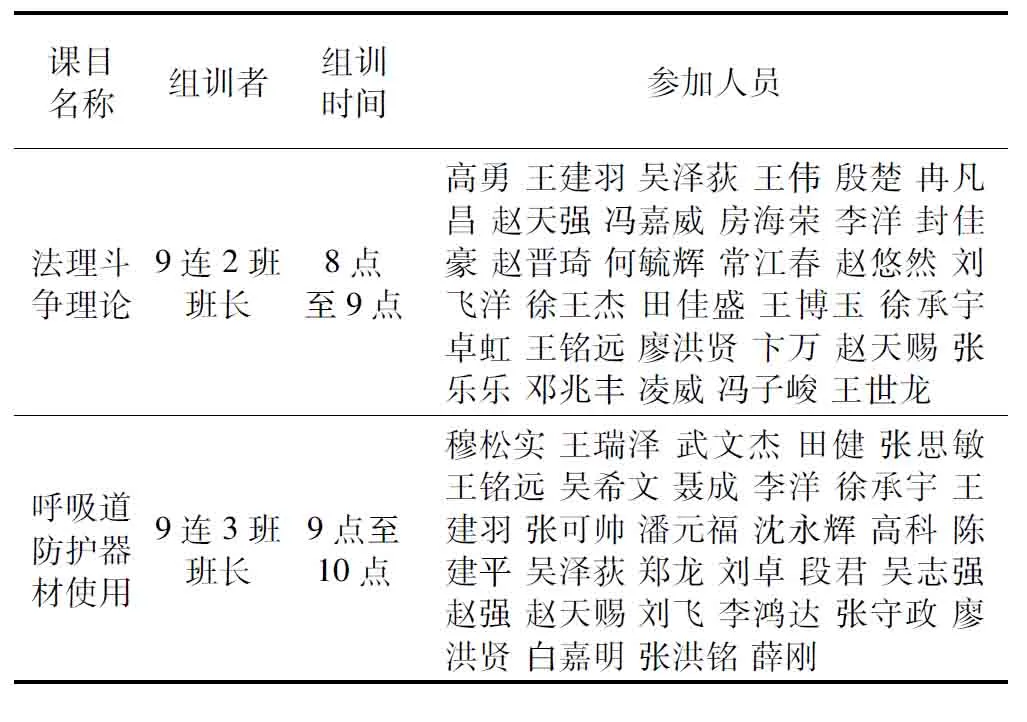
表3 补差训练计划示例

4 结束语

本文结合遗传算法和粒子群算法的优化原理,设计出兼具遗传算法优势的进化粒子群算法,并将其引入补差训练计划工程应用中,通过和同类智能优化算法的综合对比,验证了该算法的有效性,并实现了补差训练计划的智能优化。创新点有:1)根据补差训练计划工程实际,设计了符合工程特点的熵权理想点法作为多指标融合评分算法；2)设计出兼具遗传算法优势的进化粒子群算法,通过实验证明了该算法较标准粒子群算法和遗传算法收敛效率更高,能有效避免个体在游走中陷入局部最优陷阱；3)将算法引入工程项目实践中,使用效果相比于人工拟制训练计划提升明显。进化粒子群算法作为智能优化算法,具有原理易懂、结构简单的特征,不仅用于补差训练计划的智能优化,具有广泛的智能优化应用前景。