电动汽车永磁同步电机电流谐波抑制研究

林巨广 吴仕统

（合肥工业大学，合肥 230009）

主题词：永磁同步电机 谐波电压注入 电流谐波抑制 前馈控制 多同步旋转坐标系

1 前言

永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）是新能源汽车驱动系统的重要组成部分[1]。在PMSM实际运行过程中，扭矩输出质量是衡量电机性能的重要指标之一。功率器件存在死区效应及导通压降等使三相电流产生高次时间谐波；电机齿槽不对称、铁心磁饱等引起气隙磁场畸变产生空间谐波[2]。这些电流脉动使电机输出扭矩平滑度下降[3]，对定子绕组和铁芯的损耗增大[4]。

国内外学者针对这两种谐波开展了大量研究。对于时间谐波：文献[5]、文献[6]基于PMSM定子电压模型，通过计算谐波电压分量抵消相电流中高次谐波，但电压模型主要针对隐极电动机，对于凸极电动机并不适用；文献[7]、文献[8]在电流控制环上并联谐振控制器达到抑制电流畸变的效果，但易造成不同频率谐波之间相互干扰且可能增大其他频率谐波量；由于d、q轴变量之间存在耦合，文献[9]采用自动搜索算法进行交叉搜索实现解耦，并实现对d-q轴电压的前馈补偿；文献[10]利用坐标变换原理得到d-q轴变量分离计算公式进行前馈控制；文献[11]根据测试信号和测量的速度谐波实现最佳谐波电流设计，以实现转矩脉动最小化；文献[12]应用遗传算法优化定子谐波电流幅度和相位角，以减小峰值转矩波动。

针对三相电流畸变引起电机扭矩输出脉动的问题，本文提出一种电流环并联前馈电压的控制策略，前馈控制能够提高系统动态响应速度并有效防止超调。针对时间谐波，如负序5次、正序7次谐波[10]，利用n次坐标系下n次谐波分量为直流量，进行谐波电流提取、坐标变换并通过上述控制策略将谐波电压补偿量注入电机控制系统，以期达到抑制谐波电流的目的。

2 永磁同步电机电压模型

2.1 高次坐标变换原理

永磁同步电机各变量间强耦合性使控制系统较为复杂，但Park、Clark变换能使电感矩阵和PMSM数学模型得到极大简化。

为提取高次谐波电流，将1次d1-q1轴旋转坐标系变换到k次dk-qk轴旋转坐标系，由于5次谐波电流为负序，7次谐波电流为正序，所以坐标系旋转方向不同。dk-qk轴旋转坐标系下k次负序谐波电流如图1所示。

图1 k次负序dk-qk轴旋转坐标系

结合图1及Park变换推导出两相静止坐标系变换到k次dk-qk轴坐标变换矩阵为：

式中，θ为电机转子位置。

根据反Park变换矩阵推导出1次d-q轴坐标系变换到k次dk-qk轴坐标系变换矩阵为：

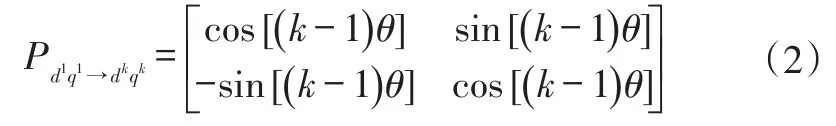
坐标系变换到5次、11次时，坐标系旋转方向和d1-q1轴旋转坐标系旋转方向相反，所以式（2）中k取负数。进行反高次坐标变换时只需将式（2）取逆可得k次dk-qk轴坐标系变换到1次d-q轴坐标系变换矩阵为：

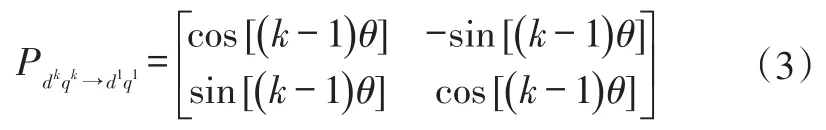
2.2 高次坐标系下PMSM谐波电压数学模型

d1-q1轴坐标系下定子电压方程为[13]：

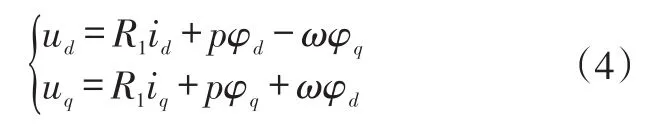
式中，R1为定子电阻；p为微分算子；ω为电角速度；φd和φq分别为d轴、q轴磁链；ud和uq分别为d轴、q轴电压；id和iq分别为d轴、q轴电流。

令k=-5，代入式（3）并在两边对t求导可得：

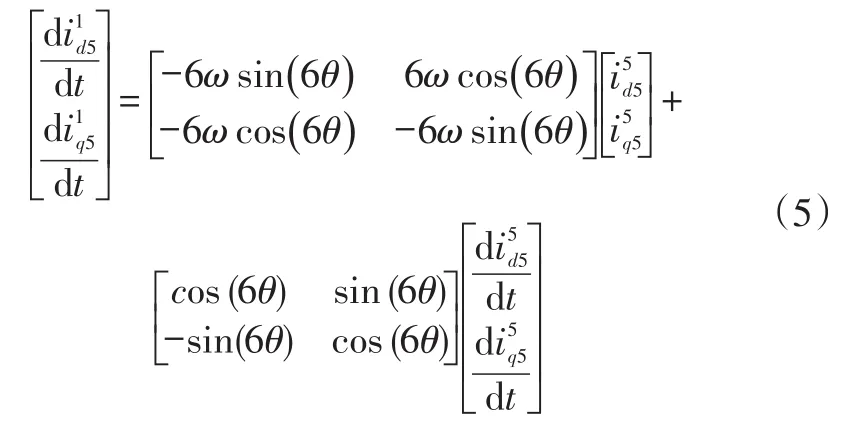
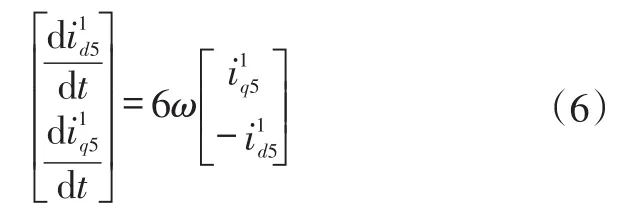
永磁体磁链φf包含φf5和φf7，即5次、7次谐波磁链，在电机高速稳定运行过程中可忽略不计。对φd和φq求导后结合式（6）代入式（4），则5次电压谐波d1-q1轴分量表示为：

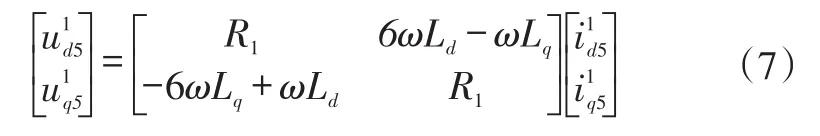
式中，Ld、Lq分别为d轴和q轴电感。

同理，7次电压谐波d1-q1轴分量表示为：

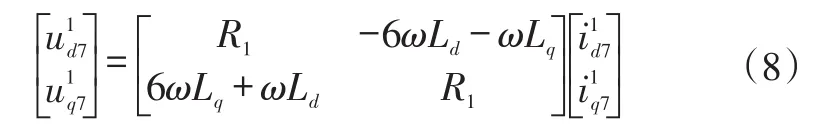
将式（7）和式（8）相加可得：

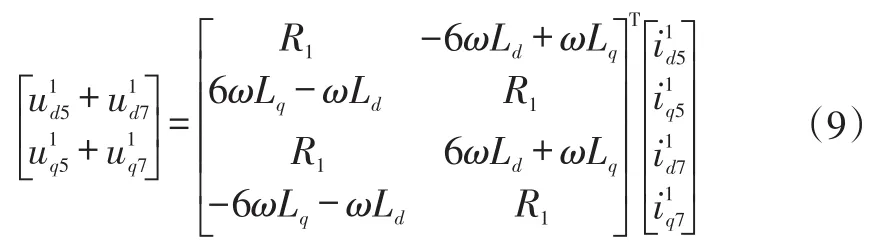
PI控制器能较好地对直流量进行追踪和调节，令式（2）中k分别取为-5和7，将id和iq转换到相应高次旋转坐标系下，同时令式（2）中k=-5，并左乘式（9），电压分量变换到5次坐标系下，提取其中与θ无关的直流量得：

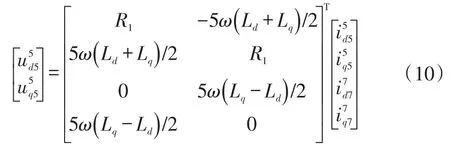
同理，令式（2）中k=7，提取其中与θ无关的直流量得：

由式（10）和式（11）可知，隐极电动机5次和7次谐波电压之间无耦合性，而凸极率ρ＞1的凸极电动机5次和7次谐波电压之间具有较强耦合性。

3 谐波注入控制策略

3.1 谐波电流提取

传统电机矢量控制系统建立在1次d-q轴旋转坐标系下，5次谐波电流提取过程如图2所示。图中，n为当前电机转速。

图2 5次谐波电流提取

利用式（2）将5次谐波电流变换为直流量，通过低通滤波器完成提取。同理可得7次谐波电流。

多数文献中低通滤波器截止频率恒定，本文采用一种基于电机实时转速的变截止频率二阶低通滤波算法，其递推差分方程为：

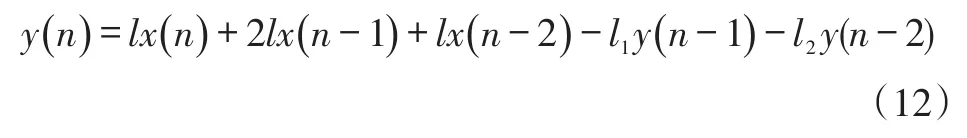
式中，x(n)、y(n)分别为当前输入变量和输出变量；tg=tan(πfc/10 000)；fc=vP/(60m)为截止频率；v为电机转速；P为极对数；m为待定系数，可以通过多次尝试仿真得到，一般取m=50。

3.2 谐波电压控制策略

文献[5]和文献[10]为提高系统死区效应灵敏度，采用主动谐波电流注入方式将5次、7次谐波电流经坐标变换后引入电机电流环，但其在实际使用中易引起较大扭矩脉动，低通滤波不彻底极易导致谐波电流注入不准确，引起更大的谐波分量，且文献[5]电压模型不适用于凸极电动机，所以在高速阶段PI控制器无法保证谐波电流注入的准确性。其次，主动谐波电流注入需要进行多次坐标变换，但数字信号处理器（Digital Signal Processor，DSP）对电流采样时刻和读取旋转编码器输出位置信息的时刻不一致，存在延迟时间Δt，使坐标变换过程的重要参数θ不准确，所以应尽量减少坐标变换次数。

本文的控制策略以谐波电压前馈控制为基础，并联5次、7次谐波电流环，既能提高系统灵敏度，又能避免上述问题，如图3所示。谐波补偿电压计算模块利用式（10）得到5次谐波电压d、q轴补偿量，并联2个PI控制器，以为控制目标，将电流环控制输出结合前馈电压补偿量得到5次谐波电压。前馈控制在保证谐波电压注入准确性的同时提高系统响应速度。同理，可以得到7次谐波电压。

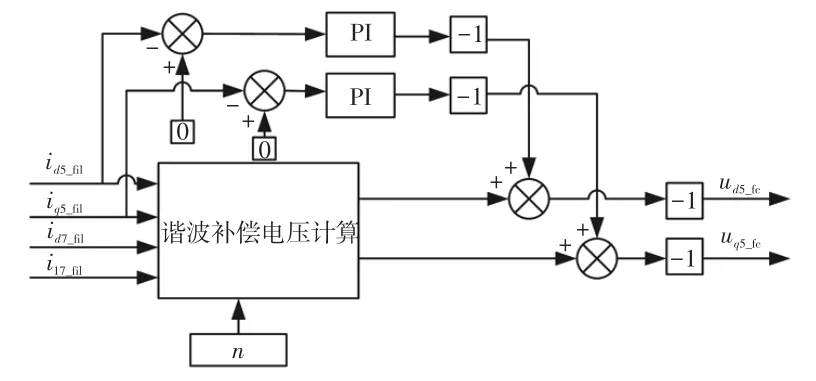
图3 5次谐波电压控制

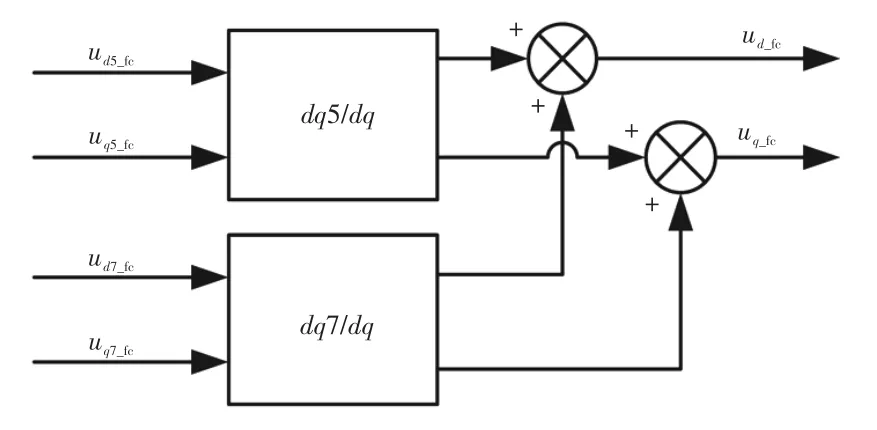
图4 5次、7次谐波电压坐标变换

综上所述，本文提出的控制策略在传统电机矢量控制系统基础上增加抑制相电流畸变的谐波电压注入模块，并基于最大转矩/电流曲线（Maximum Torque Per Ampere，MTPA）进行弱磁控制，最后将谐波电压ud_fc和uq_fc注入相应的d、q轴，完成整个谐波电压注入系统的构建，如图5所示。

4 仿真及试验

4.1 仿真及结果分析

为验证控制策略有效性，搭建了MATLAB/Simulink模型，通过设定逆变器死区时间和功率器件导通压降产生高次谐波电流。选用凸极式永磁同步电机，其参数如表1所示。

在扭矩50 N·m，转速1 500 r/min工况下，加入谐波电压注入算法前、后U相仿真电流波形以及5次、7次d、q轴旋转坐标系下相对应的电流对比如图6、图7所示，谐波幅值抑制效果对比如表2所示。

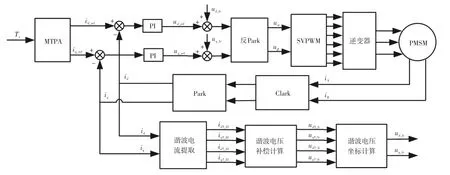
图5 谐波电压注入控制系统

表1 永磁同步电机及逆变器仿真参数

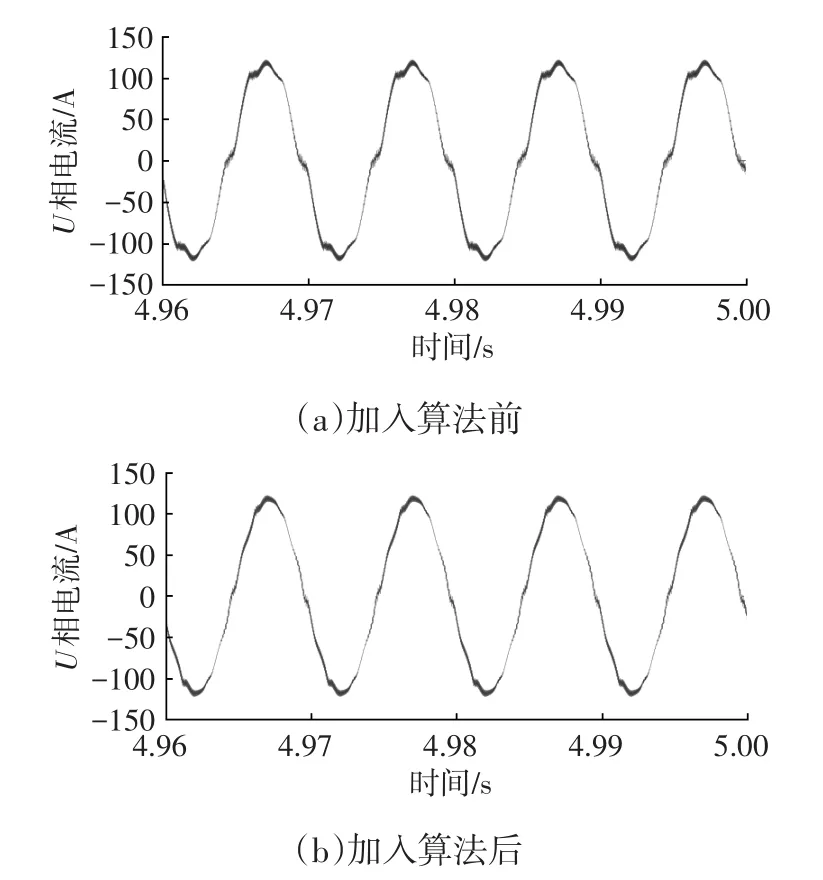
图6 U相电流仿真对比

对比图6a、图6b可知，加入谐波电压注入算法后，电流波形畸变改善明显，趋于理想正弦波形。

将U相电流进行快速傅里叶变换得到电流频谱。加入算法后总谐波失真率（Total Harmonic Distortion，THD）由8.72%降低至2.49%。其中11、13次谐波幅值可能会略有增大是由于d、q轴坐标系下12次谐波相位偏差较大，导致整个闭环控制系统不准确，但不影响整体谐波抑制效果。

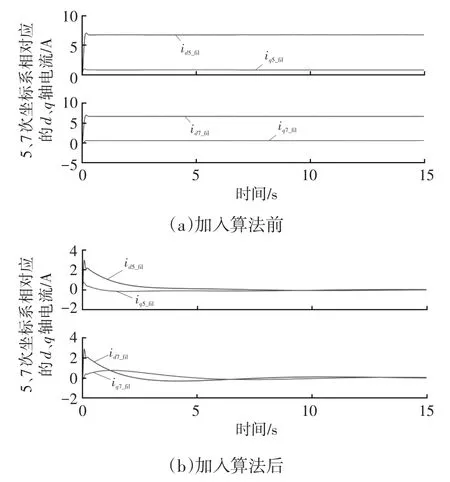
图7 5次、7次d、q轴电流对比

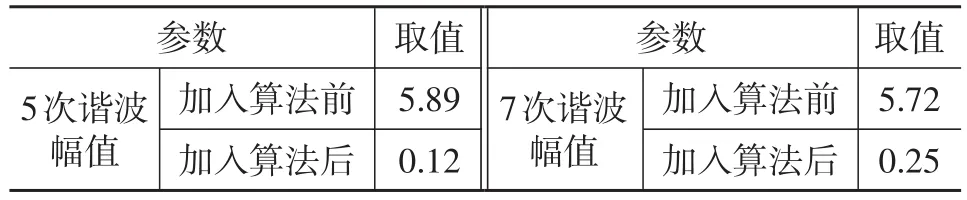
表2 U相电流谐波抑制效果对比 %

为进一步验证算法的抑制效果，分析不同转速、扭矩下U相电流5次谐波幅值减小比例，结果如图8所示。由图8可知，3 000 r/min以内谐波幅值减小比例在95%左右，但谐波幅值抑制效果随电机转速提高逐渐变差，其原因一方面在于受到逆变器开关频率限制，另一方面在于电机在高速阶段谐波产生量较低。

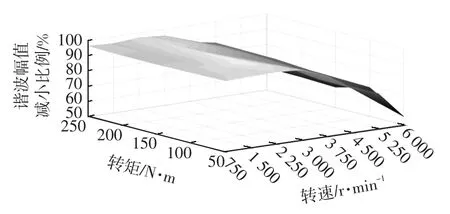
图8 5次谐波电流抑制效果变化趋势

4.2 试验结果分析

为进一步验证算法有效性，搭建如图9所示的试验平台，PMSM及逆变器参数如表3所示。

图9 试验平台

表3 永磁同步电机及逆变器试验参数

转速1 000 r/min、轻载工况下，加入算法前、后U相电流波形如图10所示，谐波抑制效果对比如表4所示。由图10可知，加入算法后U相电流波形更接近正弦，畸变程度下降。由表4可知，THD从11.88%降低至3.28%。因电机三相不对称产生3次谐波，文献[6]也指出电机本体气隙磁场严重畸变会产生2次、4次谐波。

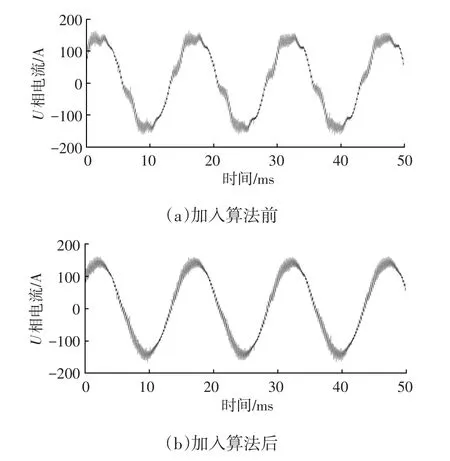
图10 试验U相电流波形对比

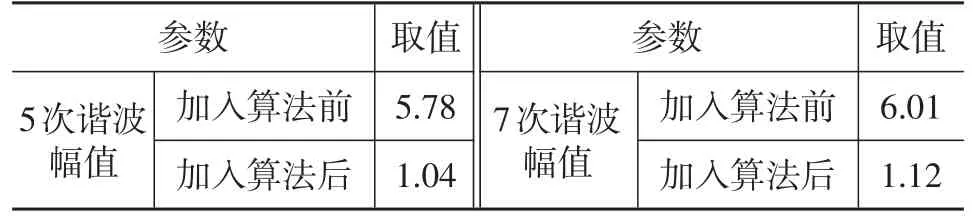
表4 试验U相电流谐波抑制效果对比 %

5 结束语

为提高永磁同步电机相电流正弦度，改善转矩输出品质，本文提出谐波电压注入方法抑制相电流中5次、7次谐波。建立高次旋转坐标系下适用于隐极、凸极式永磁同步电机电压模型，采用实变截止频率二阶低通滤波算法进行谐波电流提取，以前馈电压控制为基础并联d、q轴电流作为电流环控制对象，将谐波电压注入电机控制系统，仿真和试验结果表明，该算法能够大幅降低相电流谐波分量，减少高次谐波对电机的负面影响。