基于工况传递路径分析的汽车路噪优化方法研究

廖毅 罗德洋 余义 王田修 程果

（上汽通用五菱汽车股份有限公司，柳州 545000）

主题词：路噪 工况传递路径 重相干性分析 奇异值分解

1 前言

汽车的振动与噪声主要包括风噪、动力及传动系统噪声和路噪。相比于传统汽车，纯电动汽车没有发动机噪声，故在低频噪声中路噪所占比例最高，因此，电动汽车对路噪控制的要求比传统汽车更高。

国内外学者运用传递路径分析（Transfer Path Analysis，TPA）方法对路噪进行了研究。余雄鹰等人[1-4]运用TPA方法建立了路噪传递路径模型，解决了路噪问题，但利用TPA分析路噪需拆卸零件，改变了整车状态的边界条件且工作量大，在实际工程上难以实施[2]。为解决以上问题，伍先俊等人[5]对工况传递路径分析（Operational Transfer Path Analysis，OTPA）的理论进行了推导并成功解决了车内噪声问题；仲典等人[6-7]运用OTPA方法辨识车内噪声源，并且将重相干性分析与奇异值分解应用于OTPA，提高了工况传递路径模型的精度。上述研究运用OTPA方法主要解决了动力及传动系统的噪声问题，没有针对路噪问题进行分析，而路噪与动力系统噪声存在明显差异。

为此，本文利用OTPA方法进行路噪优化，形成一套系统的路噪优化方法，并将该方法应用于某电动汽车路面噪声开发过程，验证了其可行性与实用性。

2 工况传递路径分析理论

2.1 基本理论

为克服传统TPA方法的弊端，将传递函数用响应之间的传递率代替。目标点响应可以表示为载荷位置响应所引起的输出，其中，响应点的函数表达式为：

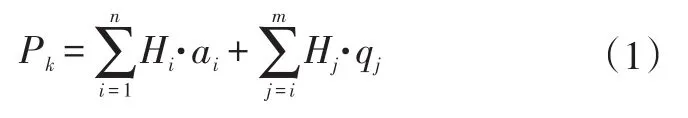
式中，Pk为响应点声压级函数；Hi为第i个位置振动加速度到响应点声压级之间的传递函数[5]；ai为结构传递路径在被动侧的工况加速度响应；qj为空气声源附近的声压级响应；Hj为第j个参考位置声压级到响应点声压级之间的传递函数。

根据文献[5]，可以将式（1）改写为矩阵形式：

式中，Y为响应矩阵；X为激励矩阵；T为传递率函数矩阵。

式（2）可推导得到：

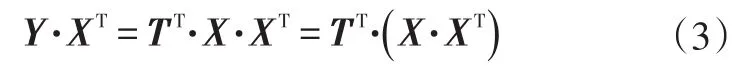
因此，传递率为：

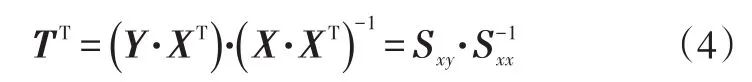
式中，Sxy为输入与输出信号之间的互功率谱矩阵；Sxx为输入信号的自功率谱矩阵。

OTPA方法的计算式中不包含载荷信息，所以不需要进行载荷识别，也不需要测量系统的传递函数及拆解零件，只需在运行工况下测定输入、输出部分的加速度和噪声响应信号即可得到系统的振动-噪声传递关系，因此该分析方法可以简化试验过程，节约测试时间和试验成本。

由式（4）可知，传递率函数有解的条件是输入信号的自功率谱矩阵可逆，即为满秩矩阵。受结构耦合的影响，各条传递路径之间存在相关性，因此需要对多输入单输出系统进行重相干性分析与奇异值分解，以保证每条传递路径的相干性与传递路径的完整性[8]。

2.2 重相干性分析

为了提高OTPA方法的准确性，在建立OTPA模型时应确保没有重要传递路径（或激励源）被遗漏，同时要解决输入信号相干性对计算结果的影响，因此利用重相干分析确认OTPA模型中的输出是否由模型中输入引起。

相干性分析是分析输出信号的频率与各输入信号特征频率之间的关系，在一个多输入单输出线性系统中，对于输出信号与输入信号，有：

式中，γ2为系统的重相干函数；Syy为输出信号的自功率谱；Sxy为输入信号与输出信号的互功率谱；Mi为多输入信号的频响函数。

通常，根据重相干函数是否大于0.9来判断输入信号是否足够来表征系统的输入状况。然而，在实际工程应用中，很难保证在整个分析频率中重相干函数均达到0.9以上。考虑实际情况，只要求所关注的频率段重相干函数大于0.9，对于其他频率段可以不考虑重相干函数的大小。

2.3 奇异值分解

为了使系统的传递率矩阵有解，要求输入信号的自功率谱矩阵各行应互不相关，因而对自功率谱矩阵进行非奇异性分析，确定独立声源或振源的数量。

设自功率谱矩阵为Q，对其进行奇异值分解：

式中，U、V分别为左、右奇异矩阵，均为酉矩阵；∑为奇异特征值的对角矩阵；σi(1≤i≤n)为自功率谱矩阵的第i个奇异值，特征谱符合从大到小排列的顺序，即σ1＞σ2＞…＞σn，共n个奇异值。

通过奇异值分解即可确定独立振源或声源的位置和数量，保证OTPA模型传递路径的完整性，从而保证其精确性。

3 基于OTPA的路噪优化方法

利用OTPA方法进行路噪优化，该方法主要分为路噪问题确认、工况传递路径分析和路噪优化等3个步骤，具体流程如图1所示。

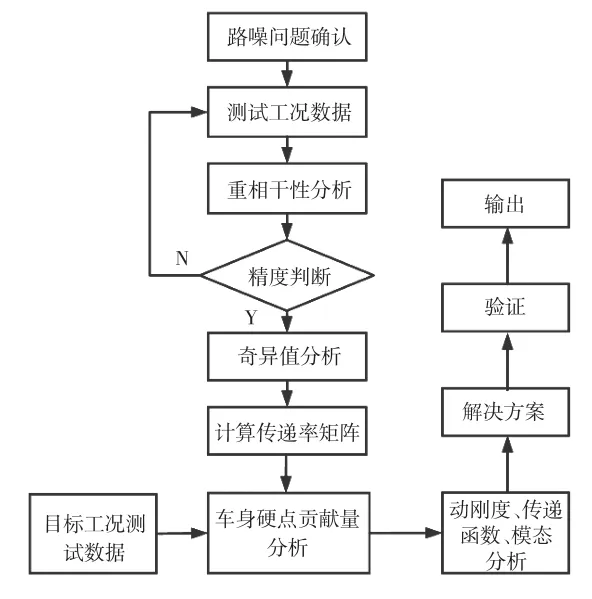
图1 基于工况传递路径分析的路噪优化方法

首先进行路噪问题确认，通过测量得到车内声压级频谱，确认问题是否由路面激励引起。一般在粗糙水泥路面上以60 km/h的车速匀速行驶测量车内噪声，同时也需测量滑行工况下的车内噪声，对比主要峰值是否在同一水平。若峰值基本相当，则可以判断其为路面激励引起的路噪，对比路噪目标值即可确定问题点。

其次，进行工况传递路径分析，以缩小路噪问题的排查范围，分析步骤如下：

a.通过测量得到激励点的加速度信号与响应点的声压级信号，形成多输入单输出的OTPA模型。为保证OTPA模型的传递路径不被遗漏，应测量出所有的激励点。

b.分析多输入单输出的OTPA模型重相干性，通过重相干性判断模型的精度，对于关注的频率段，重相干性一般要求大于0.9，若重相干性均小于0.5，则重新测量数据，以保证传递路径不被遗漏。

c.对激励矩阵进行奇异值分解，以排除各条传递路径间的相互耦合，求解出正确的传递率矩阵。

d.根据OTPA理论计算出各传递路径的传递率矩阵，测量目标工况激励点的激励矩阵，计算得到各激励点的贡献量。第i个激励点的贡献量Pi为：

式中，Xi为第i点的激励；Ti为第i点到响应点的传递率。

最后进行路噪优化。按照激励点贡献量的大小进行排序，对贡献量大的激励点进行原点动刚度、噪声传递函数及模态分析，得出对应的方案并进行验证。

4 基于OTPA的路噪优化与应用

4.1 路噪问题确认

某纯电动汽车在粗糙路面上以60 km/h的速度行驶时，主观感受低频路噪较大，通过测试驾驶员右耳处声压级，得到声压级频谱曲线如图2所示。由图2可看出，在频率为42 Hz附近的声压级峰值超过55 dB(A)，对低频轰鸣影响较大，确定频率为42 Hz是主要问题点之一。

图2 驾驶员右耳处声压级频谱

4.2 工况传递路径分析

为快速找出引起低频路噪的主要传递路径，建立了如图3所示的OTPA模型，按OTPA模型进行传感器布置，每个激励点布置1个三向加速度传感器。

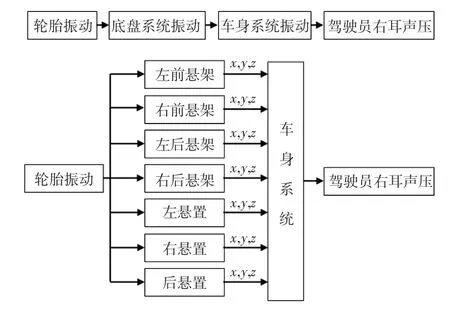
图3 OTPA模型

4.3 路噪分析

通过对后悬置被动侧到驾驶员右耳处的噪声传递函数（Noise Transfer Function，NTF）分析和车身内饰模态分析发现，顶盖前横梁模态与电池包安装模态在频率为42 Hz时耦合，模态耦合会导致振动幅值增大，从而导致低频声压级变大。同时，后悬置z向噪声传递函数在频率为42 Hz处存在峰值。为改变这一频率附近的模态振型，降低后悬置z向噪声传递函数，需要对电池包支架进行加强，如图4所示，将电池包的1～4号支架厚度由2.0 mm增加至3.0 mm。电池包支架加强后，频率42 Hz附近的呼吸振型消失，后悬置z向传递函数下降10 dB以上，如图5所示。

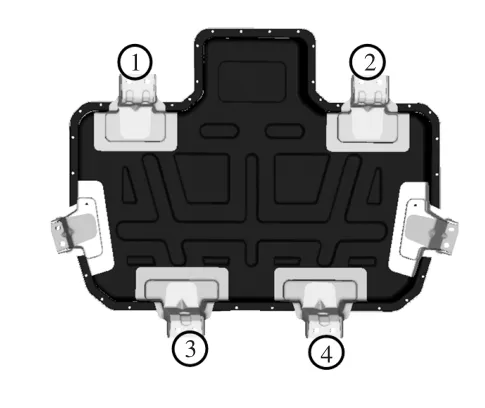
图4 电池包1～4号支架加强

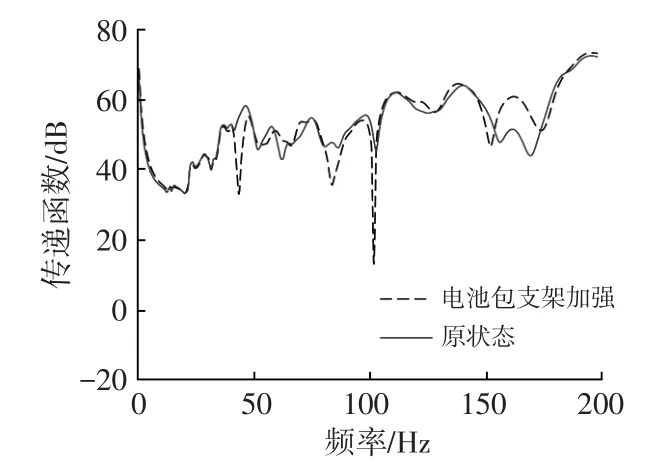
图5 电池包支架加强前、后噪声传递函数分析

为验证改进方案的有效性，对改进后的车辆进行车内噪声测试，并与改进前进行对比，结果如图6所示。由图6可看出，频率42 Hz附近的声压级从57.94 dB(A)下降至56.05 dB(A)，同时，40～140 Hz处的声压级也不同程度下降，低频噪声的主观感受也得到了大幅提升，表明改进方案效果明显。

图6 电池包支架加强前、后声压级频谱曲线对比

5 结束语

本文提出了一种基于OTPA的路面噪声分析方法，可对问题原因进行快速识别，且克服了传统传递路径分析工作量大、效率低的问题。将该方法运用于解决某电动车路噪问题，快速排查出了主要原因并提出了优化方案，采用优化方案后，该电动车声压级峰值降低了1.9 dB(A)以上，低频噪声主观感受得到大幅提高，验证了该方法的可行性与实用性。