归一化互信息量最大化导向的自动阈值选择方法
邹耀斌 雷帮军 臧兆祥 王俊英 胡泽海 董方敏
图像阈值分割由于具有简洁性、直观性和有效性等特点而被持续关注[1−5].阈值分割的基本原理是将图像中每个像素的灰度值与选择的阈值进行比较,然后确定像素是属于前景还是背景.选择阈值由此成为阈值分割的关键[6],而让所选阈值尽可能地接近最优阈值则是阈值分割的核心目标[7].
在阈值的自动选择方面,一类思想是以概率统计学和/或信息论为基础,利用灰度直方图提供的原始信息和/或派生信息计算阈值.根据灰度直方图的维度以及构建灰度直方图过程中所涉及到的图像空间,可以将灰度直方图分为全局一维直方图,局部一维直方图,全局联合直方图三大类.
全局一维灰度直方图通过对整幅图像的灰度值分布进行统计而建立.利用全局一维灰度直方图的典型方法包括Otsu方法[8]、最小误差法[9]、最大香农熵法[10]、最小交叉熵法[11]以及基于非香农熵的方法[12−15].这些方法虽然适合分割灰度直方图为双峰模式且峰谷特征明显的图像,但是容易误分割灰度直方图为单峰模式的图像.一些新近提出的方法[16−21]尝试在全局一维灰度直方图范围内对相关方法进行改进,但是它们面临着一个共同的难题:对于全局一维灰度直方图相同但是图像内容不同的两幅图像,它们无法计算出不同的阈值.
局部一维灰度直方图通过对图像特定区域的灰度值分布进行统计而建立.典型的特定区域是前景和背景之间的过渡区[22−25],其一维灰度直方图具有近似对称分布的倾向[7].这种倾向性虽然降低了局部一维灰度直方图退化为单峰模式的风险,但同时也弱化了直方图的峰谷特征.另外,为了获取过渡区的局部一维灰度直方图信息,需要先提取出合理的过渡区,这会引发如何自动评估未知特征参数的新难题.
全局联合灰度直方图通过对原始图像和其派生图像的灰度值进行联合分布统计而建立.派生图像可以是原始图像的均值滤波或者中值滤波结果[26−33],也可以是原始图像的阈值化分割结果[34].限于计算复杂度,目前全局联合灰度直方图的维度主要是二维[26−30]和三维[31−33].在利用全局联合灰度直方图进行阈值分割方面,由卢振泰等[34]提出的结合k均值和互信息量(Combiningk-means and mutual information,CKMI)的方法颇具特色.然而,CKMI方法倾向于选择这样的二值图像:值为0的像素个数和值为1的像素个数的差尽量小(具体分析见第1节).这种倾向性使得CKMI方法很容易误分割前景和背景大小不平衡的图像.
上述方法大多限于分割具有近似双峰模式或者近似单峰模式直方图的图像,并且相对而言,它们一般更适合于处理前景和背景的灰度分布可以用正态分布近似逼近的情形.然而,灰度直方图所呈现的模式是复杂多变的.除了双峰和单峰模式外,还有无峰和多峰模式.另外,构成每种直方图模式的基本分布又有多种可能,除了正态分布外,还有常见的极值分布、瑞利分布、贝塔分布和均匀分布等.当前景或背景的灰度分布呈现为极值分布、瑞利分布、贝塔分布、均匀分布或者它们的混合分布时,如何自动选择出合理的分割阈值是个新难题.
为了在统一框架内处理上述不同灰度分布情形下的阈值选择问题,提出了一种归一化互信息量最大化导向(Maximizing normalized mutual information,MNMI)的自动阈值选择方法.MNMI方法比较不同阈值分割图像所对应的轮廓图像和一幅多尺度梯度乘图像的归一化互信息量,并以最大的归一化互信息量所对应的阈值作为最终分割阈值.实验结果表明,当前景或背景的灰度分布可以用正态分布、极值分布、瑞利分布、贝塔分布、均匀分布或者它们的混合分布逼近时,MNMI方法计算出的阈值比4个新近开发的方法所得阈值在总体上更优.
剩余内容安排如下:第1节先简介CKMI方法,然后剖析该方法的主要缺陷;第2节提出MNMI方法,并从理论上阐述了该方法所具有的优势;第3节讨论MNMI方法和5个被比较方法的实验结果;第4节给出结论.
1 CKMI方法及其缺陷
1.1 计算阈值的目标函数
CKMI方法主要包括两个步骤:第一步用k均值算法计算出一个初始阈值tinitial,第二步是在[tinitial−δ,tinitial+δ]范围内,以最大化原始图像和二值图像之间的互信息量为目标,搜索一个更优的最终阈值tfinal.卢振泰等[34]建议δ=10.
记原始图像为X,使用一个阈值t∈[tinitial−δ,tinitial+δ]阈值化X,并记阈值化所得二值图像为Yt.CKMI方法的第二步使用如下目标函数计算最终阈值tfinal:
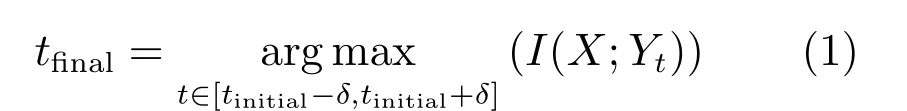
其中,I(X;Yt)表示计算X和Yt之间的互信息量.对于两幅具有相同大小的图像X和Yt,可以用式(2)计算它们之间的互信息量[34]:
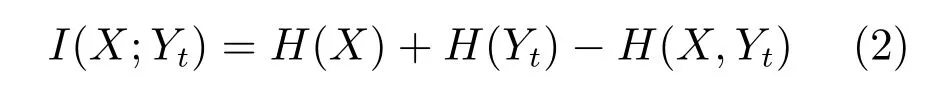
其中,H(X)和H(Yt)分别是X和Yt的香农熵,而H(X,Yt)是X和Yt的联合香农熵.
1.2 目标函数的化简
下面将证明CKMI方法的目标函数,即式(1),可以被化简为:
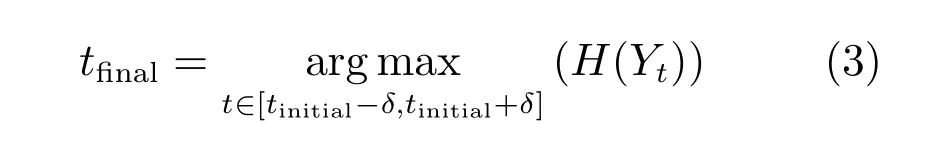
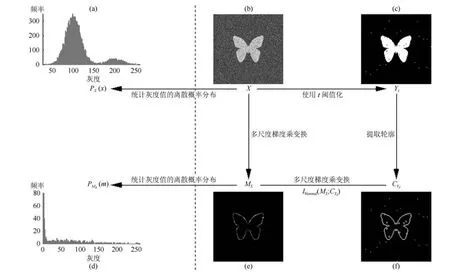
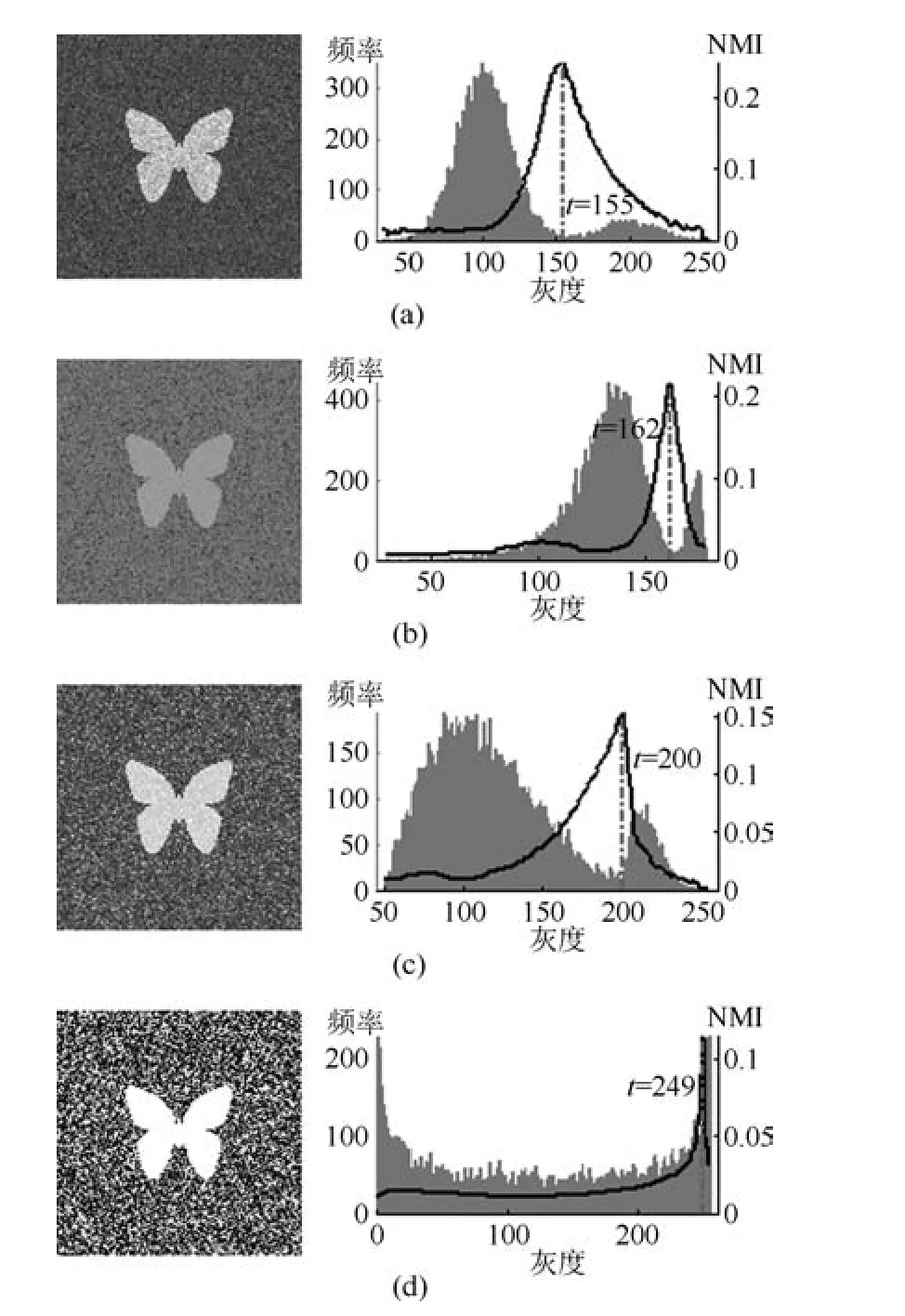
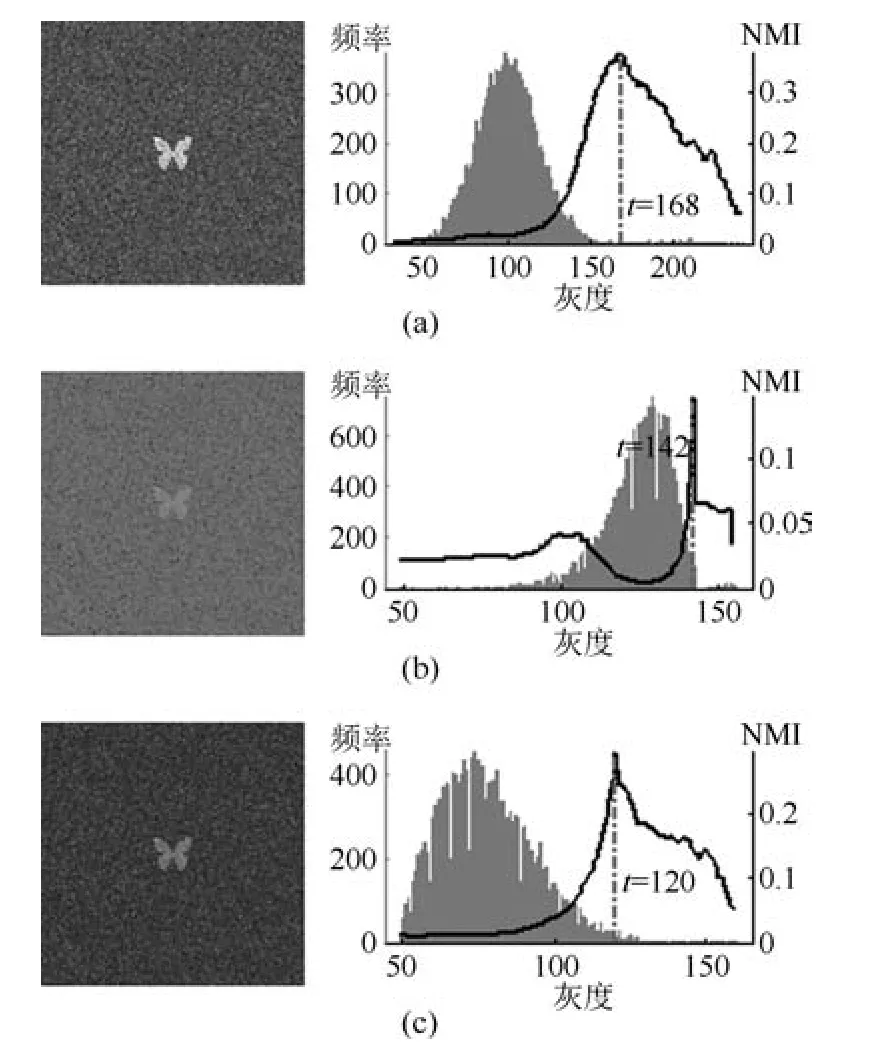
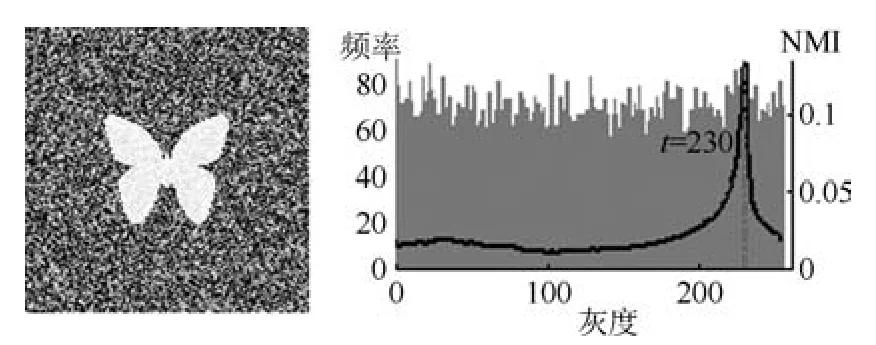
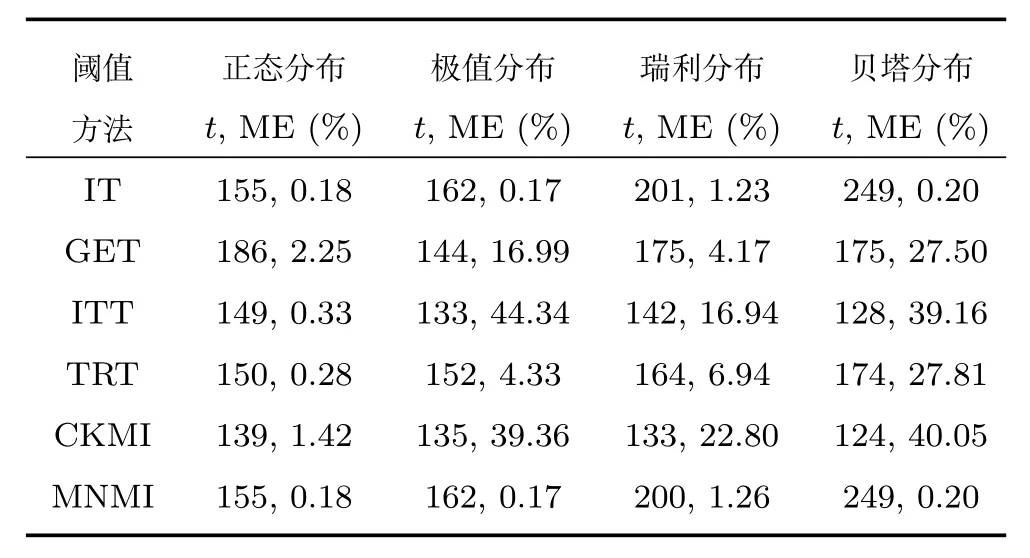
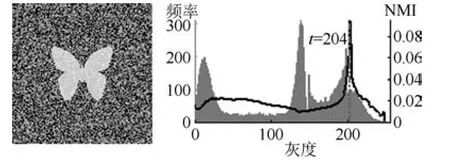
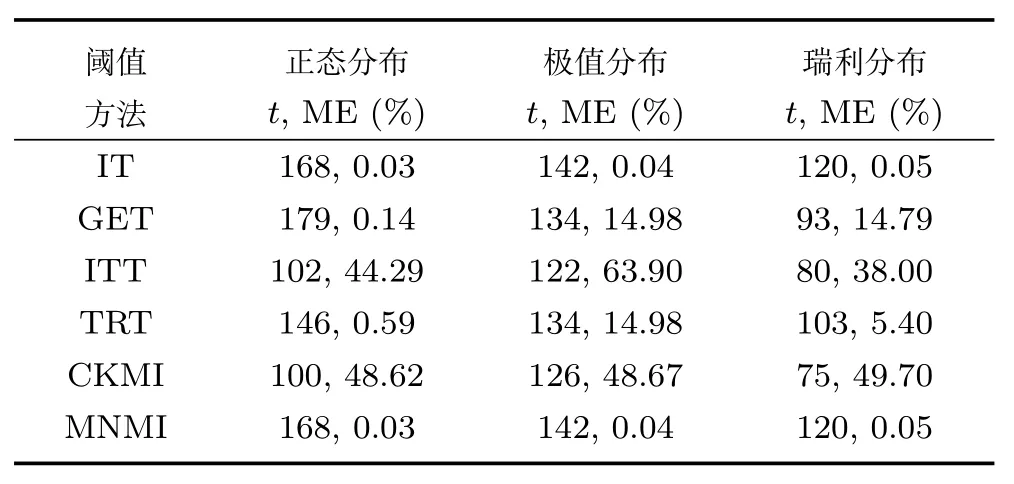
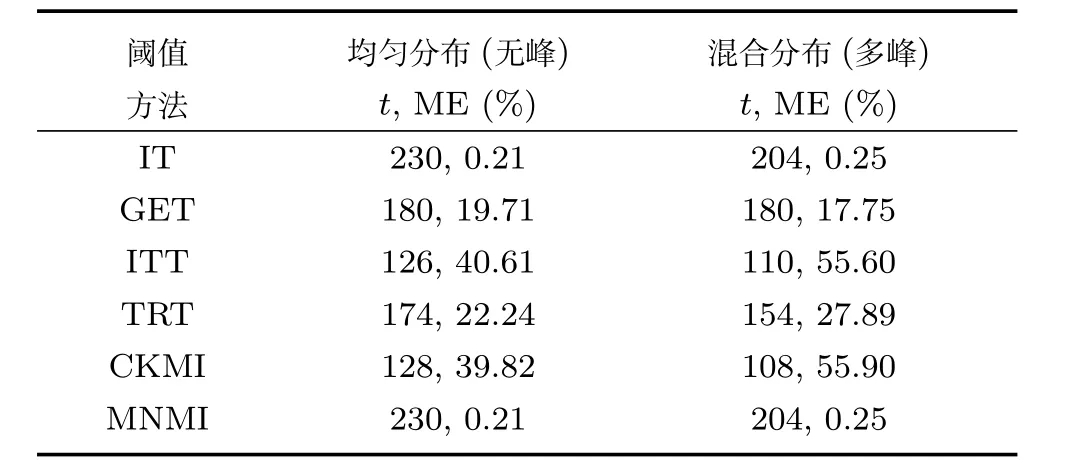
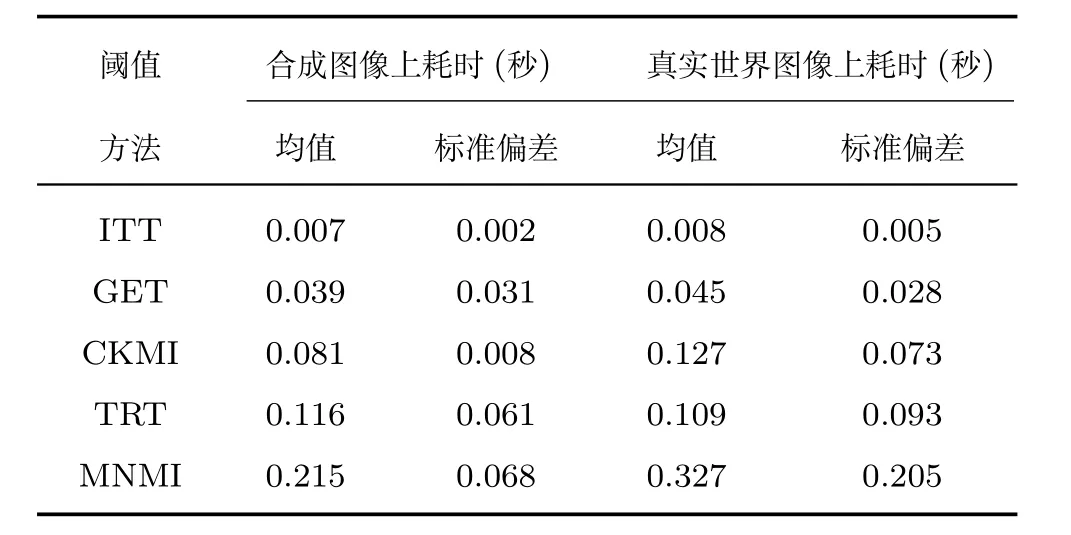
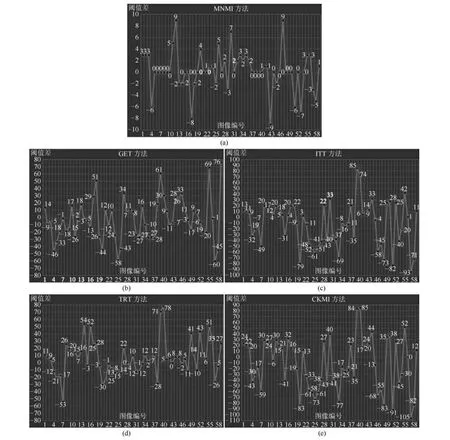
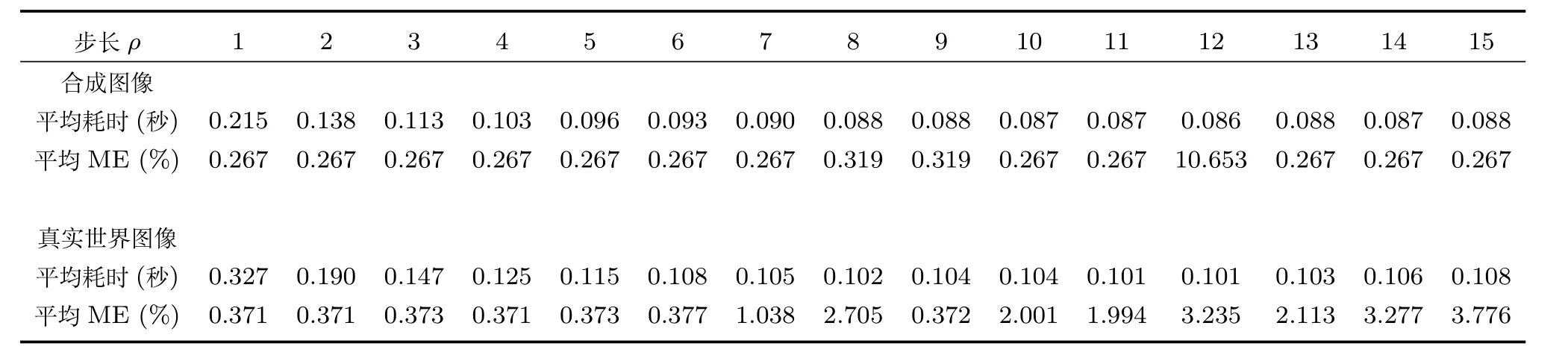
证明.由于二值图像Yt的像素值为0或1,则图像X和Yt的联合灰度分布PX,Yt(x,y)与图像X的灰度分布PX(x)有如下特殊关系:1)当x 在CKMI方法中,第一步采用了k均值算法.如果k均值算法估计的初始阈值tinitial严重偏离最优阈值,以至于一个小的δ值无法让区间[tinitial−δ,tinitial+δ]包含最优阈值.此时CKMI方法的第二步将无法在区间[tinitial−δ,tinitial+δ]内搜索到最优阈值. 退一步讲,假设扩大δ取值使得区间[tinitial−δ,tinitial+δ]包含最优阈值,那么CKMI方法将依赖式(1)计算最终阈值tfinal.由式(1)到式(3)的化简过程,可知这等效于使用式(3)计算最终阈值tfinal.根据香农熵的定义,式(3)中的H(Yt)可以展开为: 其中,p表示Yt中像素值为0的概率,而1−p则是Yt中像素值为1的概率.H(p)和p的关系是:1)0 情形1.如果区间[tinitial−δ,tinitial+δ]内的任意阈值t阈值化原始图像X,所得二值图像Yt对应的p值都小于0.5,则由于0 情形2.如果区间[tinitial−δ,tinitial+δ]内的任意阈值t阈值化原始图像X,所得二值图像Yt对应的p值都大于0.5,则由于0.5 情形3.如果区间[tinitial−δ,tinitial+δ]内的任意阈值t阈值化原始图像X,所得二值图像Yt对应的p值部分小于0.5,部分大于0.5,则式(3)将使得最终分割阈值tfinal具有这样的特性:在tfinal阈值化原始图像所得二值图像Ytfinal中,值为0的像素个数和值为1的像素个数的差尽量小. 对于情形1,如果最优阈值小于tinitial,那么tinitial+δ会误分割更多像素.对于情形2,如果最优阈值大于tinitial,那么tinitial−δ也会误分割更多像素.退一步讲,假设情形1(或情形2)所得阈值tinitial+δ(或tinitial−δ)比tinitial更优或者就是最优阈值,则会引发一个新问题:对不同的图像如何自动计算出不同的δ.没有证据表明这个问题会比自动计算阈值本身更容易.卢振泰等[34]建议δ=10,除了减少计算代价的解释外,没有关于δ=10的其他深入分析.此外,在上述3种情形下,CKMI方法将不管前景像素和背景像素的实际比例,只是去力求:在最终分割结果图像中,值为0和值为1的像素个数尽可能相等.这种倾向性使得CKMI方法只适合处理前景和背景大小较为均衡的图像.一旦前景和背景的大小失衡,CKMI方法将产生明显的误分割,这点也被后面的实验所证实. MNMI方法采用如下目标函数计算最终阈值tfinal: 式(6)拓展了t的取值范围,由CKMI方法中的[tinitial−δ,tinitial+δ]拓展为[tmin,tmax],其中,tmin和tmax分别表示原始图像的最小灰度值和最大灰度值.这种拓展使得MNMI方法:1)不需要k均值算法去估计初始阈值tinitial;2)不需要考虑额外的参数δ;3)避免了CKMI方法中区间[tinitial−δ,tinitial+δ]不包含最优阈值的可能性. 式(6)中的MX表示对原始图像X进行多尺度梯度乘变换后所得图像(图1(b)和(e)分别给出了X和MX的直观示意).MX在像素位置(r,w)处的值可以按如下式(7)计算[7]: 图1 MNMI方法所涉及的关键概念和步骤的图示((a)原始图像X 的灰度直方图;(b)原始图像X;(c)使用t阈值化原始图像X所得的二值图像Yt;(d)对原始图像X进行多尺度梯度乘变换后所得图像MX的灰度直方图;(e)图像MX;(f)从二值图像Yt中提取轮廓后所得轮廓图像CYt.注意,为了能更清楚地显示灰度区间[0,255]内灰度值出现的频率,(d)中灰度直方图在频率为80处进行了截断.)Fig.1 Graphic illustration of crucial concepts and steps in MNMI method((a)Gray level histogram of original image X;(b)original image X;(c)binary image Ytobtained by thresholding original image X with a gray level t;(d)gray level histogram of image MXproduced by applying a multiscale gradient multiplication transformation to original image X;(e)image MX;(f)contour image CYtextracted from binary image Yt.The gray level histogram in(d)is truncated at the frequency 80 for more clearly showing the frequency of gray level in the range[0,255].) 式(6)中的CYt表示二值图像Yt对应的轮廓图像(图1(c)和(f)分别给出了Yt和CYt的直观示意).CYt可如下获得:首先让CYt等于Yt,然后对Yt中每个值为1的像素进行判断,如果该像素的四邻域均为1,则设置该像素在图像CYt中对应位置的像素值为0. 式(6)中的Inormal(MX;CYt)表示计算图像MX和图像CYt的归一化互信息量.由于MX和CYt具有相同大小,可以应用式(8)计算两者之间的归一化互信息量[35]: 式中,H(MX)和H(CYt)分别是MX和CYt的香农熵,而H(MX,CYt)是MX和CYt的联合香农熵. 其次,MNMI方法将原始图像X变换成图像MX,实际上是实施了直方图规范化:将图像X的直方图规范化为图像MX的单峰长拖尾直方图.如图1(d)所示,图像MX的灰度直方图的峰起始于灰度值0处,尾结束于灰度值255处.这种直方图规范化有利于MNMI方法以统一的框架处理具有不同直方图模式的原始图像X.图像MX的单峰长拖尾直方图的形成源于边缘信号和噪声对FDoG滤波器不同的响应特点.随着滤波尺度的增加,边缘信号的响应值在总体上得到更好的保持,而噪声的响应值则更快地衰减.当不同滤波尺度下的响应值相乘时,绝大部分噪声的总响应值被往0处抑制,强弱不同的边缘信号的总响应值有大有小,分布在[0,255]区间.这些综合因素使得图像MX的灰度直方图具有单峰长拖尾特征. 为了更清晰地说明如何利用式(6)∼(8)计算最终阈值tfinal,这里进一步给出了实现MNMI方法的8个步骤. 算法1.算法名称:MNMI 输入.原始灰度图像X 输出.阈值tfinal及阈值分割结果图像Ytfinal 步骤1.对输入的原始图像X,分别计算出n个滤波尺度 (即σ1,σ2,···,σn) 下的 FDoG 滤波结果图像,并将这n个滤波结果图像相乘产生出规范图像MX(注:FDoG滤波系数可以预先生成并按规律存储在一个MAT文件中,做FDoG滤波时直接访问预先载入的MAT文件即可快速获得相应的滤波系数). 步骤2.统计规范图像MX的离散灰度分布,并利用该分布计算出MX的香农熵H(MX)(注:香农熵H(MX)只需计算一次). 步骤 3.遍历原始图像X的灰度区间[tmin,tmax],对于该区间内的每个灰度值t,如果它在原始图像X中出现过,则按步骤4到步骤7顺序执行.执行时,用一个变量Ifinal记录当前最大的归一化互信息量,初始时令Ifinal=0;用一个变量tfinal记录当前最大的归一化互信息量对应的灰度值,初始时令tfinal=tmin. 步骤4.对于灰度值t,使用如下规则产生一幅对应的二值图像Yt:对原始图像X的每个像素进行判断,如果X在某个像素位置(r,w)处的灰度值大于或等于t,则将Yt(r,w)设置为1,否则将Yt(r,w)设置为0. 步骤 8.输出最终的分割阈值tfinal,同时按步骤4的规则产生一幅相应的二值图像Ytfinal并输出. 实验环境配置如下: Intel Core i3-2350M 2.3GHz CPU,4GB DDR2内存,Windows 7操作系统,Matlab 2009a编程平台.测试图像集包含具有不同灰度分布模式的9幅合成图像和59幅真实世界图像,每幅测试图像的分割参考图像借助于Adobe Photoshop CS软件手工产生(请访问https://pan.baidu.com/s/1bo9QNH9下载测试图像、分割参考图像和分割参考图像的制作说明). 采用误分类率 (Misclassification error,ME)[3,7]来定量评估分割方法的分割精度.ME是定量评估分割精度的一个常用指标,反映了分割结果图像中背景像素被误分为前景像素,以及前景像素被误分为背景像素的情况,其计算公式为: 其中,Fg和Bg分别表示分割参考图像中的前景和背景,而Ft和Bt分别表示使用t阈值化原始图像所得二值图像中的前景和背景.符号T表示取交集运算,符号|·|表示计算元素的个数.当阈值化所得二值图像和分割参考图像相同时,ME等于0%;当阈值化所得二值图像和分割参考图像完全相反时,ME等于100%. 提出的MNMI方法和交互式阈值(Interactive thresholding,IT)方法[36]、广义熵阈值(Generalized entropy thresholding,GET)方法[15]、迭代三类阈值(Iterative triclass thresholding,ITT)方法[19]、过渡区阈值(Transition region thresholding,TRT)方法[7]以及CKMI方法[34]进行了比较.值得注意的是,IT方法人工交互式选择一个阈值,该阈值对应的二值图像具有最小的ME值.因此,IT方法可以作为其他比较方法在分割精度方面的参考. 9幅代表性合成图像被用于检验6个分割方法对不同直方图模式的适应能力.在这9幅图像中,4幅图像的灰度直方图呈现出双峰特征(见图2),3幅图像的灰度直方图呈现出单峰特征(见图3),1幅图像的灰度直方图呈现出无峰特征(见图4),1幅图像的灰度直方图呈现出复杂的多峰特征(见图5). 在灰度直方图呈现出双峰特征的4幅图像中,各有1幅图像的前景或背景的灰度分布呈现为正态分布(见图2(a))、极值分布(见图2(b))、瑞利分布(见图2(c)),以及贝塔分布(见图2(d)).表1显示:1)对双峰正态分布情况,GET和CKMI方法的分割结果比其他4种方法差.特别是GET方法,其计算出的阈值和IT方法选择的阈值相差31个灰度级.2)对双峰极值分布、瑞利分布和贝塔分布三种情况,GET、ITT、TRT和CKMI方法的分割精度明显下降,它们各自计算出的阈值和IT方法选择的阈值的平均绝对偏差分别达到39,69,40和73个灰度级,反映在ME值方面,GET、ITT、TRT和CKMI方法在这三种情况下的平均ME值分别达到了16.22%,33.48%,13.03%和34.07%.3)对双峰正态分布、极值分布和贝塔分布三种情况,MNMI方法和IT方法的分割结果完全一致.在双峰瑞利分布情况下,MNMI方法和IT方法所得阈值仅相差1个灰度级. 对灰度直方图呈现为单峰特征的情况,所合成的3幅图像的前景或背景的灰度分布分别呈现为正态分布(见图3(a))、极值分布(见图3(b))以及瑞利分布(见图3(c)).由于前景在整幅图像中所占比例仅为1%,因此图像的整体直方图呈现为单峰特征.表2显示:1)GET和TRT方法仅在单峰正态分布情况下获得较好的分割结果,在单峰极值分布和瑞利分布情况下误分割都较严重.2)在单峰的三种情况下,ITT和CKMI方法的ME值都超过35%,误分割非常严重.3)对单峰的三种情况,MNMI方法计算出的阈值始终和IT方法选择的阈值保持一致,因此它们的ME值也保持一致. 图2 灰度直方图呈现出双峰特征的4幅合成图像.每幅子图的左边显示了合成图像,右边显示了对应的灰度直方图,黑色曲线显示了提出的MNMI方法计算阈值的目标函数曲线,虚线及旁边的数字标示了MNMI方法计算出的阈值(下同)((a)正态分布情形;(b)极值分布情形;(c)瑞利分布情形;(d)贝塔分布情形)Fig.2 4 synthetic images with bimodal gray level histogram.In each sub- figure,a synthetic image is shown on the left;on the right,the gray level histogram is shown,the objective function of MNMI method is illustrated with a black curve,and the threshold obtained by MNMI method is indicated with a dashed line and a number(the same below)((a)Normal distribution,(b)Extreme value distribution,(c)Rayleigh distribution,(d)Beta distribution) 图3 灰度直方图呈现出单峰特征的3幅合成图像((a)正态分布情形;(b)极值分布情形;(c)瑞利分布情形)Fig.3 3 synthetic images with unimodal gray level histogram((a)Normal distribution,(b)extreme value distribution,(c)Rayleigh distribution) 图4 灰度直方图呈现出无峰特征的合成图像Fig.4 A synthetic image with a uniform distribution of gray level 表1 6个阈值分割方法在灰度直方图呈现出双峰特征的4幅合成图像上的阈值t和ME值Table 1 Threshold values t and ME values of 6 thresholding methods on 4 synthetic images with bimodal gray level histogram 图5 灰度直方图呈现出多峰特征的合成图像(灰度直方图的灰度区间[0,50]由瑞利分布和均匀分布组合而成,区间[51,100]为均匀分布,区间[101,150]由极值分布和均匀分布组合而成,区间[151,200]由贝塔分布和正态分布组合而成,区间[201,255]为正态分布)Fig.5 A synthetic image with multimodal gray level histogram(The gray level histogram in the range[0,50]is combined by a Rayleigh distribution and a uniform distribution,[51,100]by a uniform distribution,[101,150]by an extreme value distribution and a uniform distribution,[151,200]by a beta distribution and a normal distribution,and[201,255]by a normal distribution.) 表2 6个阈值分割方法在灰度直方图呈现出单峰特征的3幅合成图像上的阈值t和ME值Table 2 Threshold values t and ME values of 6 thresholding methods on 3 synthetic images with unimodal gray level histogram 表3 6个阈值分割方法在灰度直方图分别呈现出无峰特征和多峰特征的合成图像上的阈值t和ME值Table 3 Threshold values t and ME values of 6 thresholding methods on synthetic images with uniform gray level histogram and multimodal one 灰度直方图呈现为无峰特征的测试图像是通过添加均匀分布的噪声而合成的(见图4).因为无法利用双峰直方图的峰谷特征或者单峰直方图的凹陷特征,阈值化此类合成图像比阈值化前面两类合成图像更有挑战性.表3第2列数据显示:1)GET、ITT、TRT和CKMI方法计算出的阈值离最优阈值230分别差50,104,56和102个灰度级,结果这4种方法均存在较为严重的误分割.2)MNMI方法依然能精确地计算出最优阈值230,获得和IT方法一样的分割结果. 鉴于真实世界图像的灰度直方图经常呈现为多峰特征,我们也合成了一幅具有多峰特征的测试图像(见图5).注意这幅图像的前景只形成了一个峰,其余峰都是由背景所形成.因此,分割这幅图像的难度并不亚于分割具有无峰直方图特征的图像.表3第3列数据显示:1)MNMI方法和IT方法计算出相等的阈值204,两者输出一样的分割结果.2)但是GET、ITT、TRT和CKMI方法的误分割严重,它们对应的ME值分别高达17.75%,55.60%,27.89%和55.90%,它们计算出的阈值和最优阈值204分别差24,94,50和96个灰度级. 59幅真实世界图像被用于进一步检验6个分割方法对不同直方图模式的适应能力.这些测试图像的灰度直方图可用正态分布、极值分布、瑞利分布、贝塔分布和均匀分布中的若干分布的混合进行逼近.在这59幅图像中,编号1到19的图像的灰度直方图呈现出双峰特征,编号20到36的图像的灰度直方图呈现出单峰特征,编号37到40的图像的灰度直方图呈现出无峰特征,编号41到59的图像的灰度直方图呈现出多峰特征(大于等于3峰). 图6显示了6种方法在59幅测试图像上分割结果的量化比较.从该图可以观察到:1)对具有双峰特征、单峰特征、无峰特征或者多峰特征的图像,IT方法和MNMI方法对应的ME均值都小于0.6%;而其他方法,除了TRT在单峰特征情况外,每种方法在不同灰度直方图特征情况下对应的ME均值都大于4.3%;2)在灰度直方图呈现为无峰特征情况下,GET、ITT、TRT和CKMI 4种方法的误分割都很严重,各自的ME均值都超过了15%;3)ITT和CKMI方法在单峰和多峰特征情况下,误分割情况也很严重,各自的ME均值都超过了16%,并且相对而言,CKMI方法的误分割更严重;4)仅就GET、ITT、TRT和CKMI 4种方法自身比较而言,GET方法和ITT方法分别在多峰和双峰直方图特征情况下略有优势,而TRT方法则更适合分割具有单峰直方图特征的图像. IT方法以最小化ME值为标准人工交互式选择阈值,因此它选择的阈值是最小化ME值意义下的最优阈值.这样,通过比较其他方法所得阈值和IT方法所选阈值之间的差异,可以衡量其他方法在阈值计算方面的偏离程度.从图7可以观察到,MNMI、GET、ITT、TRT、CKMI 5种方法和IT方法的阈值差分别分布在区间[−9,9],[−60,76],[−93,85],[−53,78]和 [−105,85]内.这里,每个区间的上下限反映了相应方法在阈值计算方面最大可能的偏离度(针对此59幅测试图像而言).进一步,如果将大于0的阈值差称为正向阈值差,将小于0的阈值差称为反向阈值差,那么可以计算出每种方法对应的正向阈值差的均值和反向阈值差的均值,这两个均值可以用于衡量每种方法在阈值计算方面的平均偏离度.MNMI、GET、ITT、TRT和CKMI 5种方法对应的平均偏离度区间分别为 [−4.38,3.32],[−20.91,25.21],[−41.17,20.93],[−14.17,22.24]和[−48.1,30.26].这组数据直接反映了:1)GET、ITT、TRT和CKMI 4种方法计算出的阈值和最优阈值总体上相差甚远;2)总体而言,MNMI方法在不同灰度直方图模式下具有更精确的阈值计算能力,或者说,它对不同灰度直方图模式的图像具有更强的适应能力. 通过比较不同方法在相同硬件和软件条件下的CPU耗时,可以直观地反映不同方法在计算效率方面的差异.在相同的硬件和软件条件下,同一个程序在不同的时间点运行,其CPU耗时通常会有轻微的浮动.为了降低这种浮动所产生的负面效应,让每个参与比较的分割方法在同一幅测试图像上连续运行20次,并以这20次运行所耗时间的均值作为该分割方法在该测试图像上的CPU耗时.以此为基础,可以进一步计算出每个分割方法在9幅合成图像和59幅真实世界图像上CPU耗时的均值和标准偏差(见表4). 表4 5个自动阈值分割方法的计算效率比较Table 4 Quantitative comparisons of 5 automatic thresholding methods in computational efficiency 图6 6个阈值方法在59幅真实世界图像上分割精度的量化比较(在每幅子图中,各条水平虚线标示了对应情形下ME值的平均值)Fig.6 Quantification comparisons of segmentation accuracy for 6 thresholding methods on 59 real-world images(In each sub-figure,each horizontal dashed lines indicate the corresponding average ME,respectively) 如表4所示,总体而言ITT和GET两种方法的计算效率相对更高,而CKMI、TRT和MNMI 3种方法的计算效率相对更低.ITT方法只需预先统计原始图像X的灰度分布信息,然后进行相对简单的均值和方差的运行,因此它的CPU耗时最少.GET方法也需要预先统计原始图像X的灰度分布信息,不过由于它计算广义熵涉及到对数运算,因此GET方法的计算代价比ITT方法略高.CKMI方法需要一个k均值算法估计初始阈值,然后涉及到对原始图像X和二值图像Yt的香农熵和联合香农熵的计算,因此它的计算量比GET方法多一些,相应地也需要花费更多的CPU处理时间.TRT方法的主要计算代价发生在多尺度梯度乘变换和平稳过渡区计算上,而MNMI方法除了涉及多尺度梯度乘变换的计算外,还涉及二值图像轮廓提取操作,以及图像MX和CYt的香农熵和联合香农熵的计算,因此MNMI方法的计算代价最大,CPU耗时最多. 为了提高MNMI方法的计算效率,可以将计算和寻找最大归一化互信息量的目标分解为两个过程来完成:跳跃式处理和逐级式处理.在跳跃式处理过程中,对原始图像X的灰度区间[tmin,tmax],将算法1中步骤3的逐个灰度处理,改为以一定步长ρ跳跃式处理,而计算归一化互信息量的其他步骤不变.跳跃式处理过程执行完毕,输出一个灰度值ttemp,它对应于跳跃式处理过程中产生的最大归一化互信息量.然后,在逐级式处理过程中,对灰度区间[ttemp−ρ+1,ttemp+ρ−1]逐个处理,即将算法1中步骤3的灰度区间[tmin,tmax]替换为[ttemp−ρ+1,ttemp+ρ−1],而计算归一化互信息量的其他步骤不变.逐级式处理过程执行完毕,输出最终的分割阈值tfinal,它对应于灰度区间[ttemp−ρ+1,ttemp+ρ−1]内的最大归一化互信息量.如表5所示,不管是合成图像还是真实世界图像,1)当步长ρ从1变化到6时,平均CPU耗时都逐渐减少,但是平均ME值基本保持不变;2)当步长ρ从7变化到15时,平均CPU耗时基本维持稳定,但是平均ME值出现波动.这样,当步长ρ取4,5或6时,MNMI方法可以在保持分割精度的同时,在计算效率方面接近于CKMI方法和TRT方法. 图7 对59幅真实世界图像,MNMI,GET,ITT,TRT,CKMI方法和IT方法获得的阈值之差(在每幅子图中,每个黑点旁的数字标示了相应的阈值差)Fig.7 The differences between MNMI,GET,ITT,TRT,CKMI and IT methods in segmentation thresholds for 59 real-world images(In each sub- figure,the number beside each black point labels the specific difference of segmentation threshold) 表5 不同步长下MNMI方法的计算效率和误分类率Table 5 Computational efficiency and ME of MNMI method with different steps 对灰度直方图呈现为双峰、单峰、无峰或者多峰特征的图像,当前景或背景的灰度分布可以用正态分布、极值分布、瑞利分布、贝塔分布、均匀分布或者它们的混合分布逼近时,MNMI方法虽然在计算效率方面不优于GET、ITT、TRT和CKMI方法,但是MNMI方法在自动阈值选择方面具有更稳健的适应能力.MNMI方法的稳健性和适应性得益于:1)MNMI方法利用多尺度梯度乘变换进行了图像的规范化,可将具有不同灰度直方图模式的原始图像转化为具有单峰长拖尾分布特征的规范图像;2)MNMI方法计算规范图像和二值轮廓图像之间的统计相关性,兼顾了规范图像和二值轮廓图像各自提供的信息;3)MNMI方法引入基于几何均值的归一化互信息量,有利于应对二值轮廓图像中值为1的像素个数和值为0的像素个数比例失衡的情况.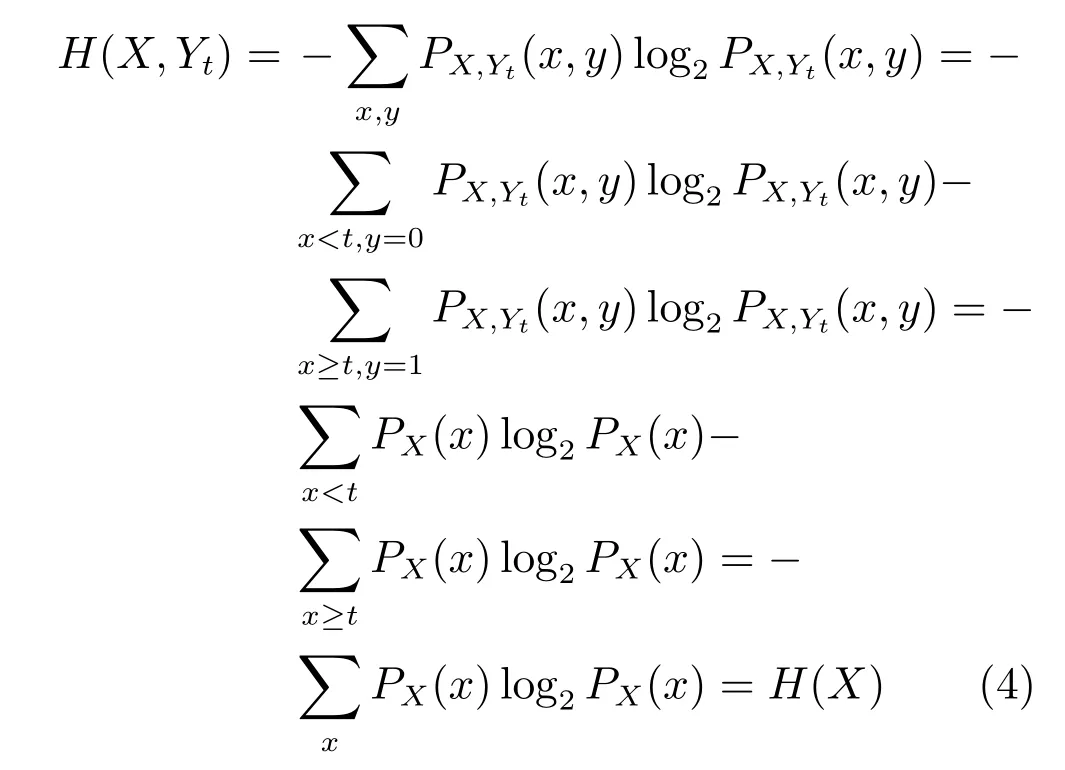
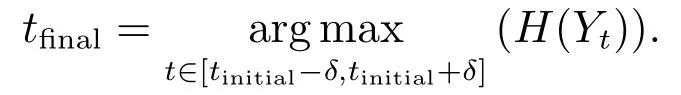
1.3 计算阈值时的缺陷
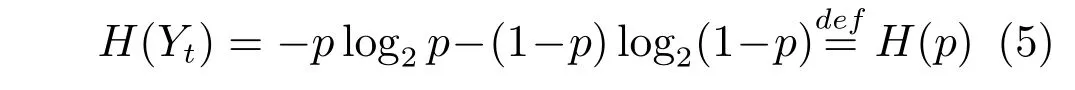
2 提出的MNMI方法
2.1 计算阈值的目标函数
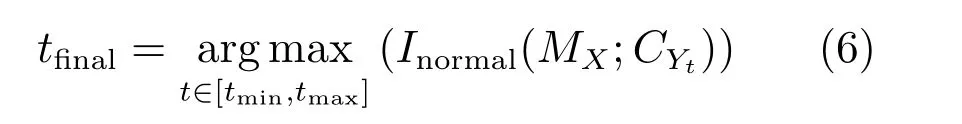
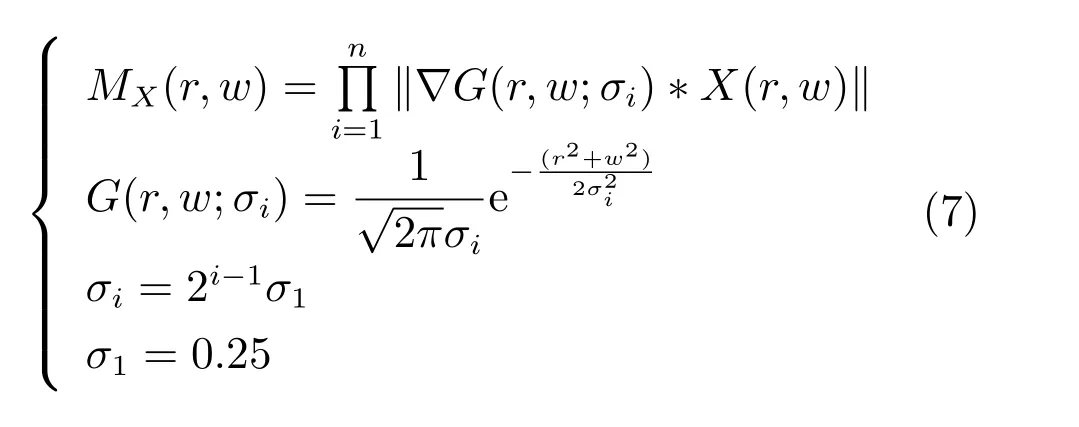
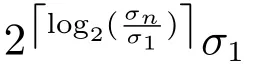
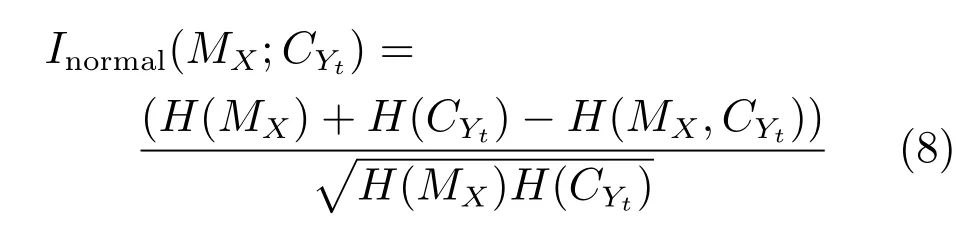
2.2 MNMI方法所具优势的理论分析
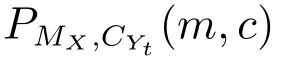
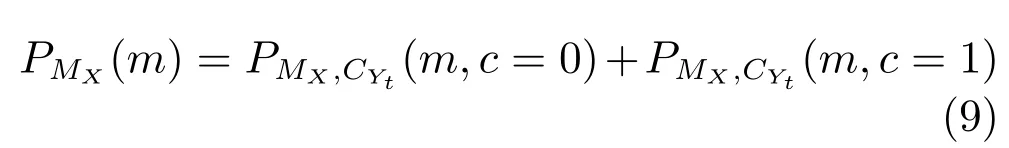
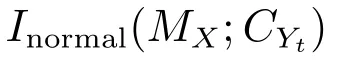
2.3 算法描述
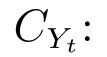
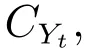
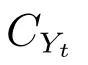
3 实验结果与讨论
3.1 实验环境、定量评估指标、参与比较的方法
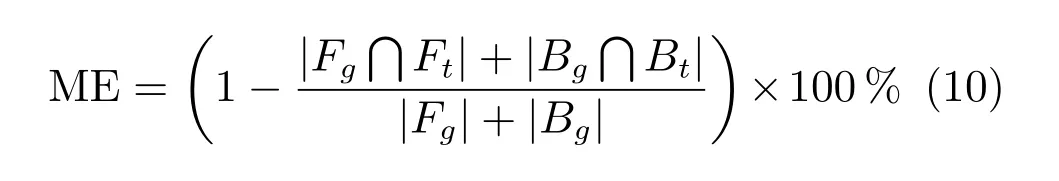
3.2 在合成图像上的比较实验
3.3 在真实世界图像上的比较实验
3.4 计算效率的比较实验

4 结论

