基于新型滑模算法的双摆旋转起重机消摆跟踪控制

欧阳慧珉 王健 张广明 梅磊 邓歆

旋转起重机作为常见的起重机械,由于其结构简单、占用空间小、无需大型行走设备等优点,因此被广泛地应用于建筑工地、矿山、港口等场合.然而,旋臂的加减速会使负载产生摆动,不仅降低了生产效率,而且会损坏货物,造成人员伤亡等.针对该问题,已经有学者作了大量的研究,并且提出了许多有效的方法[1−19].但是,当负载形状不规则或者吊钩的质量不能忽视时,该摆动会呈现出更加复杂的两级摆动现象.该现象极大地增加了系统特性分析和控制器设计的难度,因此如何设计出可以有效抑制两级摆动的控制算法问题已经成为学术界和产业界研究的难点和热点.

近年来,已经有学者针对起重机系统双摆抑制问题展开了一些研究[20−35].Tang等针对2-D双摆桥式起重机系统中由于台车运动和外部风干扰而引起的荷载摆动,提出了结合两种运动轨迹的方法,即其中一个轨迹用来抑制台车运动引起的摆动,另一个轨迹用来抑制风干扰引起的摆动,仿真与实验验证了该方法的有效性[20].陈鹤等针对双摆桥式吊车系统提出了一种时间最优轨迹规划方法,该方法在构造以时间为代价函数的基础上,将优化问题转化成非线性规划问题,通过仿真与实验验证了该方法的有效性[21].Zhang等针对双摆桥式起重机在线规划了一条台车轨道,该轨道由两部分组成分别实现双摆抑制和台车定位,仿真验证了该轨道对于参数变化和外部干扰具有鲁棒性[22].Huang等针对2-D双摆桥式起重机系统提出了一种新型指令整形方法,仿真与实验验证了该方法的有效性[23].孙宁等针对双摆桥式吊车系统提出了一种基于轨迹规划的消摆定位控制方法,该方法在充分考虑系统安全性(摆动幅值)等物理约束基础上,通过构造新颖的平坦输出信号,将施加在台车运动和两级摆动上的约束/指标转化为对平坦输出的约束,从而将轨迹规划转化为凸优化问题,通过数值仿真验证了该方法的有效性[24].Masoud等针对双摆桥式起重机系统提出了一种频率调制输入整形方法,该方法是由一个基于闭环系统的第一阶摆动频率的输入整形器和一个虚拟反馈控制环节构成,仿真与实验验证了该方法的有效性[25].Maleki等针对双摆旋转起重机系统中存在两级摆动模态的问题,提出了一种两级模态特定不敏感输入整形器,通过与两级模态零摆动输入整形器的比较验证了该方法的有效性,同时也证明了其对旋臂旋转角速度与角加速度变化具有鲁棒性[26].Masoud等针对双摆桥式起重机系统将输入整形法和闭环控制法相结合,具体而言,首先基于假设的双摆系统第一阶模态设计基础整形器,再设计一个虚拟的带有积分器反馈控制器消除由第一阶模态引起的残留摆动,通过仿真与实验验证了该方法的有效性[27].Manning等针对2-D双摆桥式起重机系统设计了一个SI2M(Two-mode specifiedinsensitivity)输入整形器,并通过与ZV2M(Twomode zero vibration)输入整形器比较验证了所提方法对于绳长变化更具有鲁棒性[28].Sung等针对2-D双摆桥式起重机系统中应用输入整形技术进行消摆控制时关于参数变化的鲁棒性问题,通过比较仿真和实验指出SI2M 整形器性能最好[29].Qian等针对双摆桥式起重机消摆控制问题,提出了一种基于SIRMs(Single-input-rule modules)的模糊控制器,比较仿真验证了该方法的有效性[30].Ouyang等提出了一种基于LMI(Linear matrix inequality)的简易鲁棒控制器解决双摆桥式起重机消摆控制问题[31].Zhang等考虑了起重机系统中参数不确定性等对控制性能的影响,提出了一个自适应控制器,系统稳定性通过李雅普诺夫定理和芭芭拉特引理进行分析,仿真结果验证了其有效性[32].Tuan等针对双摆桥式起重机消摆控制问题,提出了一个传统滑模控制器和一个多层滑模控制器,仿真结果验证了其有效性[33].Sun等针对双摆桥式起重机消摆控制问题,提出了一种饱和非线性输出反馈控制器和一种非线性准PID控制,实验结果验证了其有效性[34−35].开环控制方式[20−29],即在设计控制器时不反馈摆角信息,如轨迹规划法和基于输入整形技术已经应用于双摆桥式起重机系统.这些方法虽然具有控制器结构简单,易于实现等优点,但是它们过于依赖系统精确模型,当系统受到外部干扰后控制性能会降低.另一方面,虽然如文献[30−35]所提出的闭环控制方式可以为起重机系统提供鲁棒或自适应控制算法,但是由于它们的系统阻尼比大都设定为常数.因此很难同时实现旋臂的高精度定位和两级摆角的抑制.为此,本文将提出一种变阻尼的算法从而实现前述问题.进一步而言,不同于2-D桥式起重机的平面摆动,旋转起重机系统中的双摆均为圆锥摆,系统特性更加复杂.据笔者所知,到目前为止,尚无针对双摆旋转起重机摆角抑制的相关报道.

本文在建立双摆旋转起重机动力学模型的基础上,采用干扰观测器将其解耦成两个独立的线性系统,即起伏子系统和旋转子系统.其次,基于此线性模型分别为其设计含有非线性滑模面的滑模控制器,并通过李雅普诺夫定理分析其稳定性.最后比较仿真和定量分析验证本文所提方法的有效性.

综上,本文的主要创新之处可总结为如下几点:

1)据笔者所知,首次将具有非线性滑模面的滑模控制器应用于双摆旋转起重机系统.

2)不同于传统的线性滑模面,本文所提出的非线性滑模面可以为闭环系统提供一个可变的阻尼比,从而在提高旋臂定位精度的同时实现对两级摆角的抑制.

1 双摆旋转起重机模型

在图1所示旋转起重机模型中M0,m1和m2分别表示旋臂质量、吊钩质量和负载质量;L,l1和l2分别表示旋臂长度、悬绳长度和吊绳长度;θ1和θ3分别表示吊钩摆角和负载摆角在旋臂起伏方向上的分量;θ2和θ4分别表示吊钩摆角和负载摆角在旋臂起伏方向上的分量;θ5和θ6则表示旋臂起伏角和旋转角.

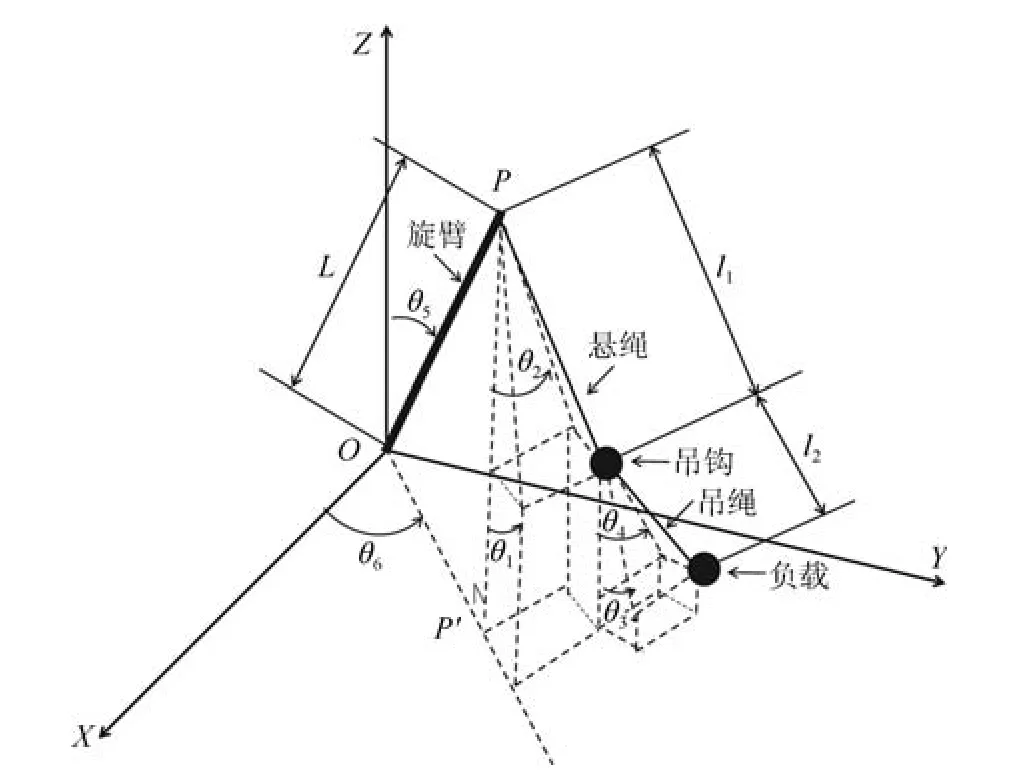
图1 双摆旋转起重机模型Fig.1 Dynamic model of double-pendulum rotary crane

为了进一步分析和设计控制系统,对旋转起重机做如下几点合理假设[1−3,6−8,28−31]:

1)吊钩和负载均看作质点,悬绳和吊绳的拉力和质量忽略不计.

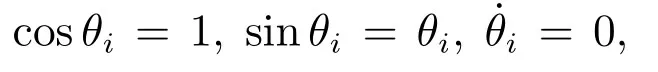
根据拉格朗日运动方程,双摆旋转起重机系统动力学模型如下所示:

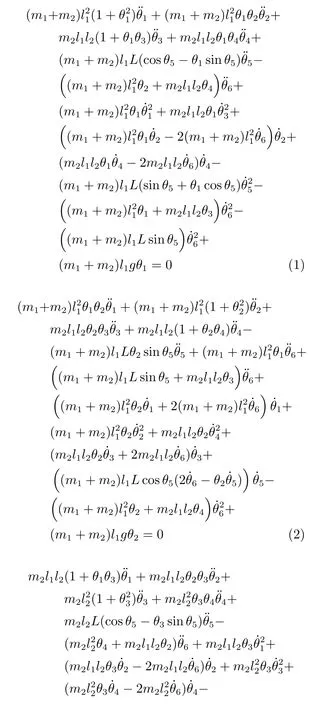
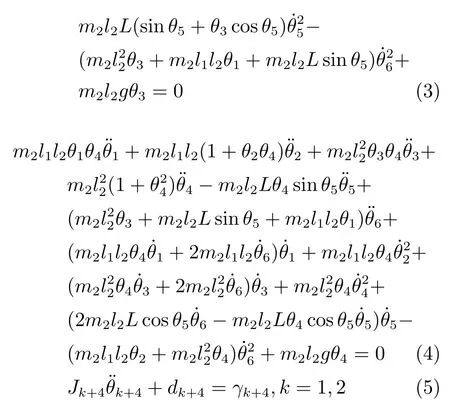
为了方便设计控制器,采用了如图2所示的干扰观测器(Disturbance observer,DOB)[11,17,36−40].

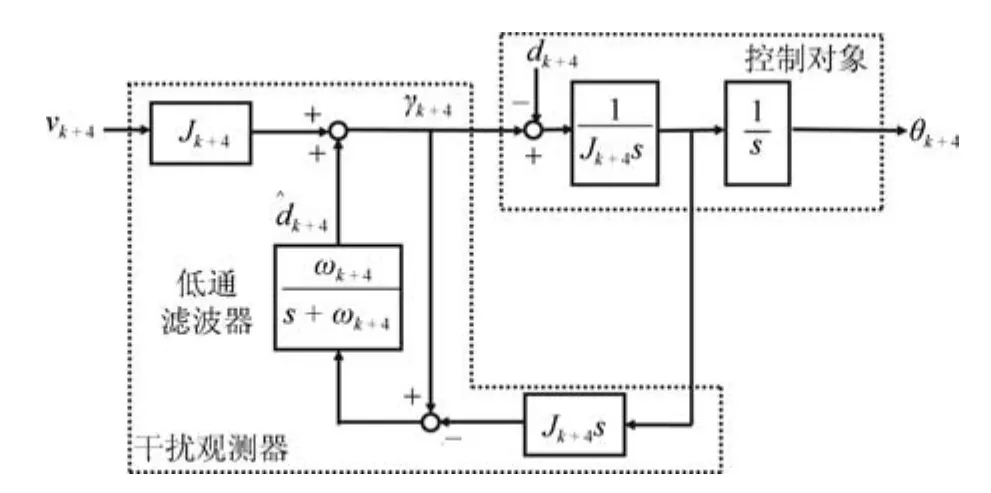
图2 含有干扰观测器的控制系统Fig.2 Control system with a disturbance observer

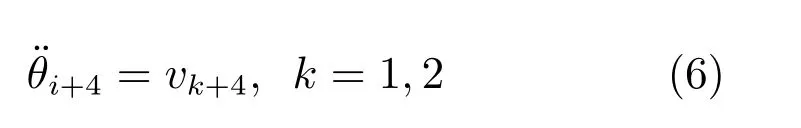
式中,vk+4表示起伏子系统和旋转子系统的控制输入.

根据前述假设,结合式(1)∼(4)和式(6),可得,

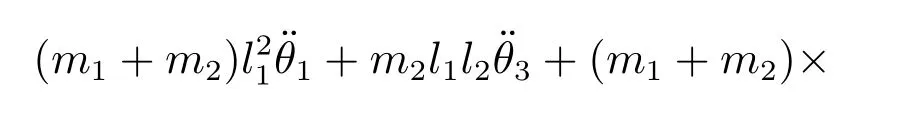
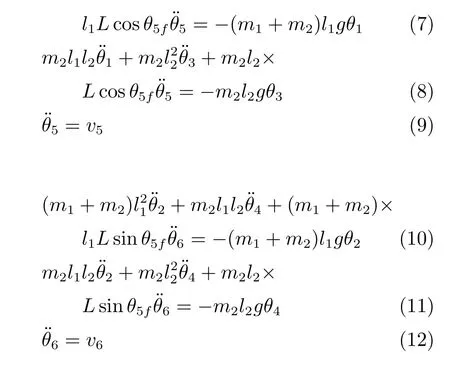
其中,θ5f为起伏角的目标值.

式(7)∼(12)写成矩阵形式可得,

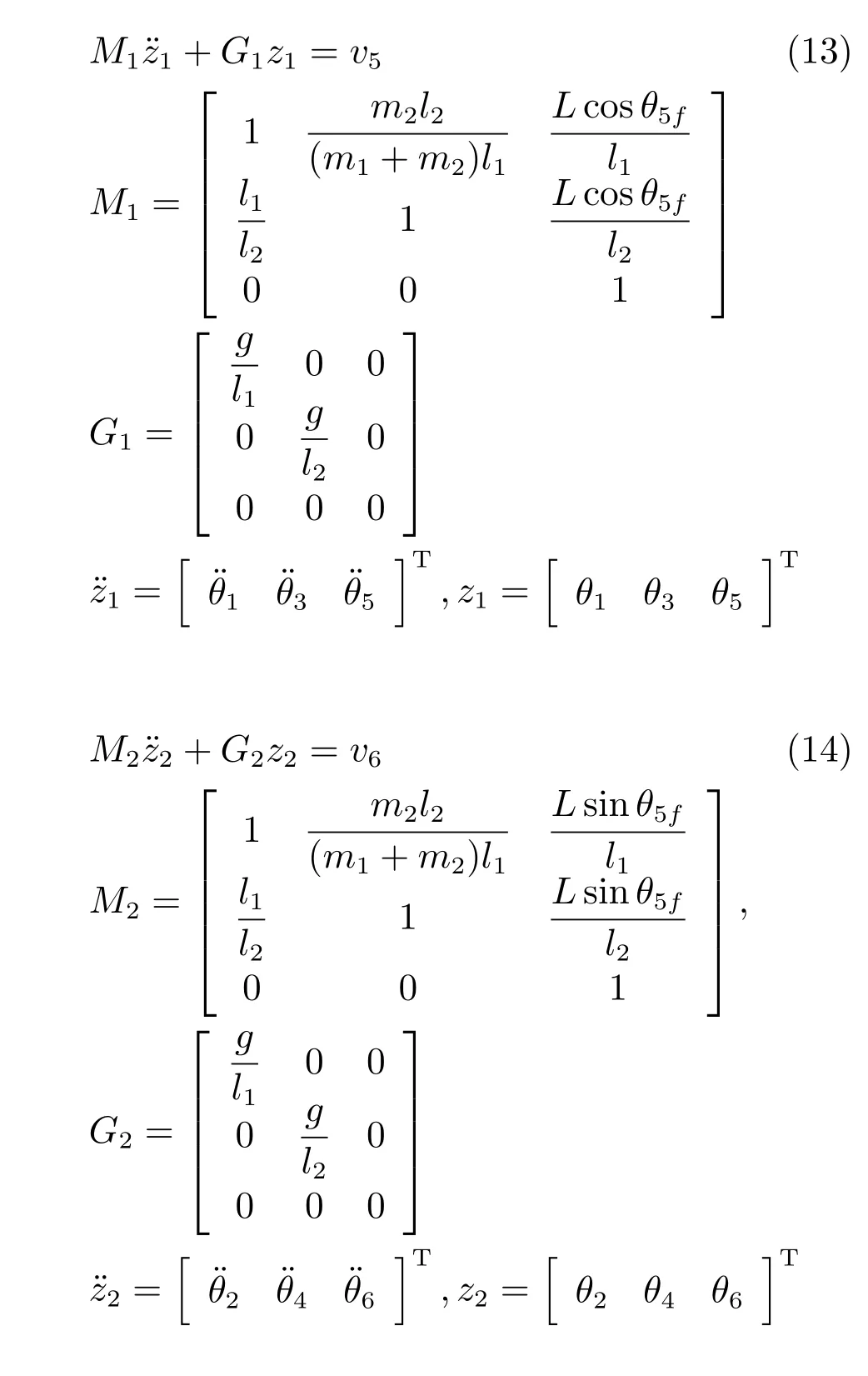
由式(13)和式(14)可知,起伏子系统和旋转子系统拥有非常相似的结构,因此本文可以为其设计相似的控制器.

2 新型滑模控制器设计和稳定性分析

2.1 含有非线性滑模面的滑模控制器设计

本节将为双摆旋转起重机设计一种新型含有非线性滑模面的滑模控制器从而同时实现旋臂高精度跟踪和摆角抑制.不同于传统的线性滑模面,本节所提出的非线性滑模面可以使闭环系统的阻尼比从最初的较小值变化为最终的较大值.较小的阻尼比可以为系统提供较快的响应速度而较大的阻尼比则可减小超调量从而使得旋臂更加精确地跟踪给定轨迹.

基于式(13)和式(14)所示起重机线性模型,本文所提出的非线性滑模面如下所示:

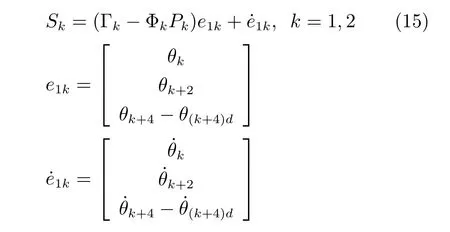
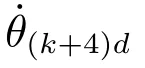
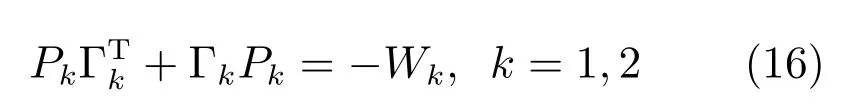
其中,Wk也是正定矩阵.选取合适的满秩矩阵Γk使得其满足赫尔维茨定理并为闭环系统提供一个较小的初始阻尼比.非线性函数Φk则要根据系统的输出(即,旋臂的起伏角、旋转角以及各方向第一、二级摆角)进行选择并可用来调节闭环系统的阻尼比.虽然该函数的选取并不唯一,但是必须满足以下两个性质:

1)必须对于系统输出可微并保证滑动模态存在.

2)必须从0变化成一个负值.

因此,本文采用如下所示的非线性函数进行控制器的设计[36]

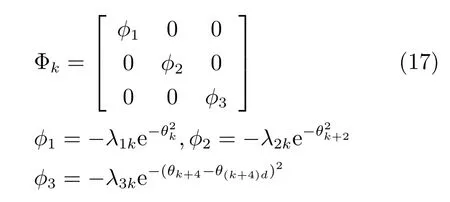
式中,λik(i=1,2,3,k=1,2) 为正值,而e(·)表示指数函数.

通过设计合适的控制律,系统的所有状态量都可以进入预期的滑模面上.当处于滑模面时,即Sk=0,可得:

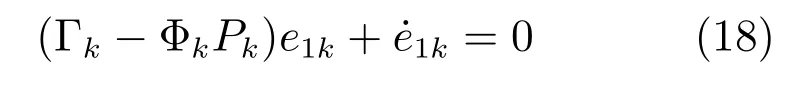
进一步整理可得:

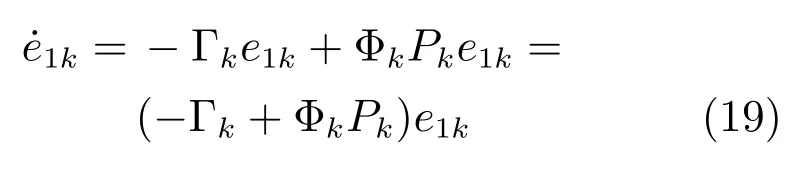
由于所设计矩阵Γk,Φk和Pk都是可逆的,因此上式所示系数矩阵也是可逆的,即该矩阵是非奇异的.

为了验证所提出滑模面的稳定性,考虑如下所示的李雅普诺夫函数:

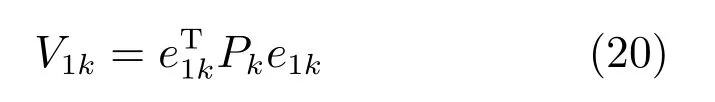
取上式一阶时间导数,可得:

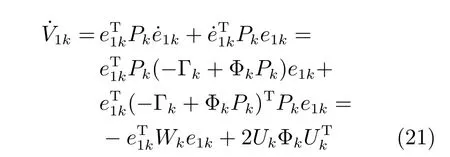
接下来,基于上述所设计的非线性滑模面并采用指数趋近律,可得:

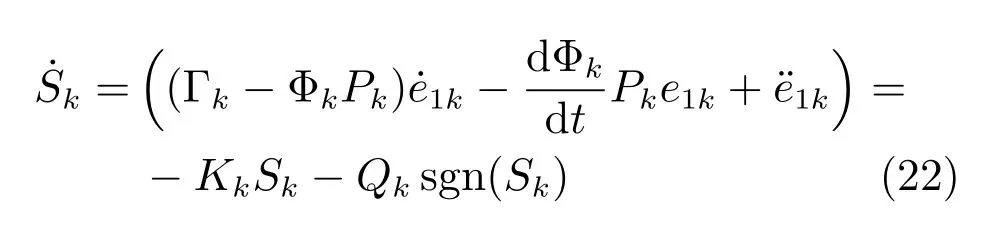
其中,Kk和Qk为系数矩阵,并满足Kk>0,Qk>0.

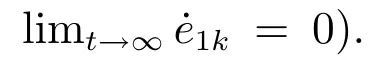
2.2 稳定性分析

本节进行系统稳定性分析,并考虑如下所示的李雅普诺夫函数:

取上式一阶时间导数,可得:

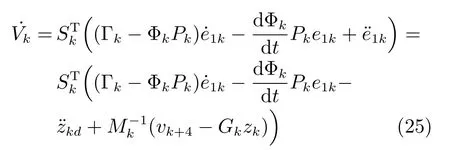
将式(23)代入式(25),可得:

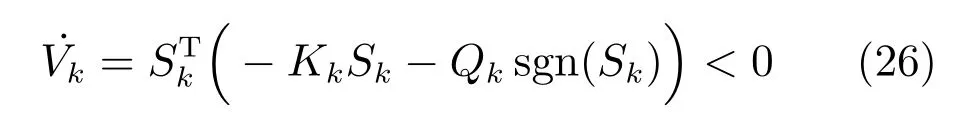
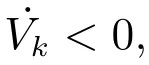
进一步,设Sk(t)初值Sk(0)>0,求解式(22)可得:

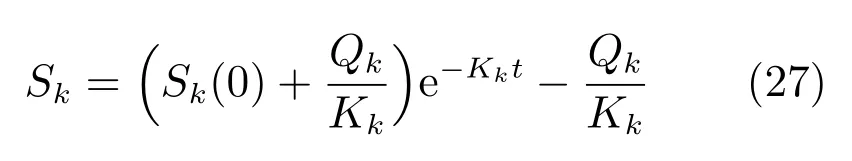
最终系统从初始状态到达滑模面(Sk=0)所需时间为,

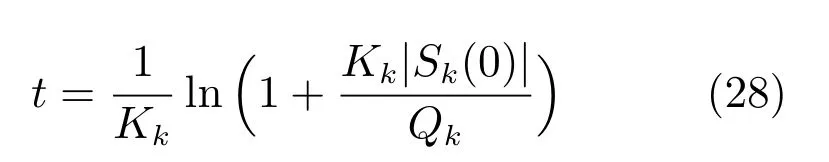
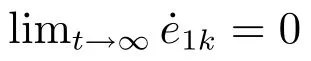
值得注意的是,由于符号函数的不连续性,式(23)所示控制器会导致系统产生抖振[33].为此,在实际应用时采用饱和函数来替代符号函数,则

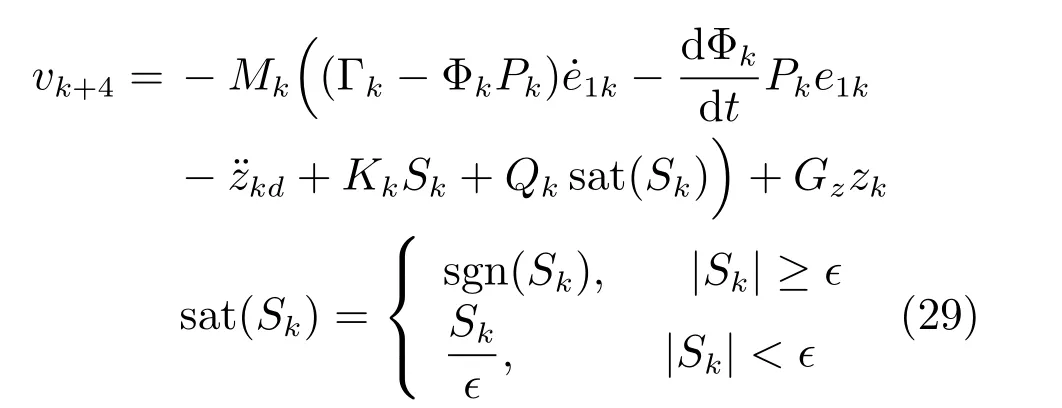
其中,†表示边界层的厚度且满足†>0.

注1.进一步讨论新控制器对系统稳定性的影响,将式(29)代入式(25),可得:

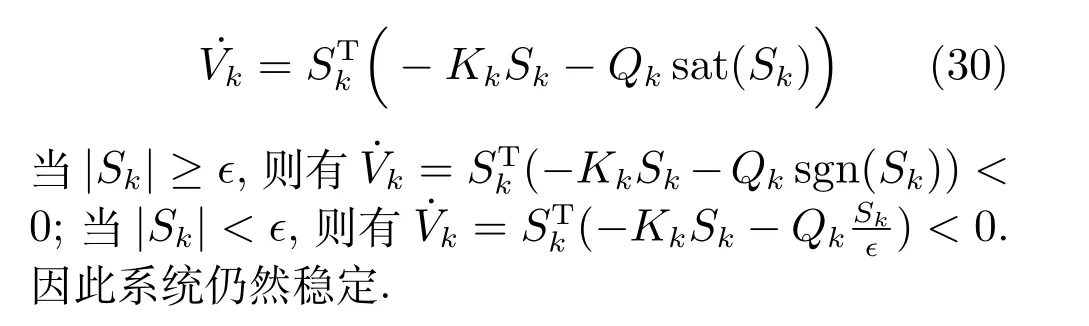
3 仿真分析结果和讨论

3.1 仿真条件

从理论上讲,阶跃信号、摆线以及输入整形曲线等均可作为旋臂的目标轨迹,从而进行控制性能的评价.然而,阶跃信号具有不连续性,容易对起重机系统造成冲击,因此在实际工程中很少直接使用.另外,当系统参数发生变化时,输入整形曲线往往需要进行重新设计.而摆线可以在初始点和终点处提供零加速度,从而减轻对系统的冲击.因此,采用如下所示的摆线作为旋臂运动的期望轨迹:

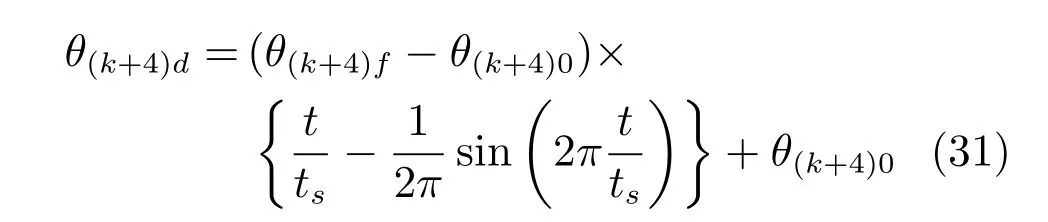
其中,θ(k+4)f,θ(k+4)0,ts和tf分别表示旋臂起伏角和旋转角的目标值,初始值,到达时间和最终时间.同时设定θ5f=40◦,θ6f=45◦,θ50=θ60=0◦,ts=3s和tf=10s,并设定当时间t属于区间(ts,tf]时,θ(k+4)f=θ(k+4)d成立.系统参数如表1所示.而控制器参数则如表2和表3所示,其中参数λik主要影响着控制性能,具体分析详见附录A.

3.2 仿真结果

本文所提方法的仿真结果和传统线性滑模面(即Φk=0)的结果进行比较.吊绳长度分别设定为l2=0.1m,l2=0.2m 和l1=0.3m.对起伏角θ5、起伏角跟踪误差e5、旋转角θ6、旋转角跟踪误差e6、摆角θ1,θ3,θ2和θ4的仿真结果分别如图3∼5所示.

表1 起重机系统模型参数Table 1 Parameters of crane system

表2 起伏子系统控制器参数Table 2 Parameters of controller in vertical subsystem

表3 旋转子系统控制器参数Table 3 Parameters of controller in horizontal subsystem

表4 定量分析(l2=0.1m)Table 4 Quantitative analysis(l2=0.1m)

表5 定量分析(l2=0.2m)Table 5 Quantitative analysis(l2=0.2m)

表6 定量分析(l2=0.3m)Table 6 Quantitative analysis(l2=0.3m)

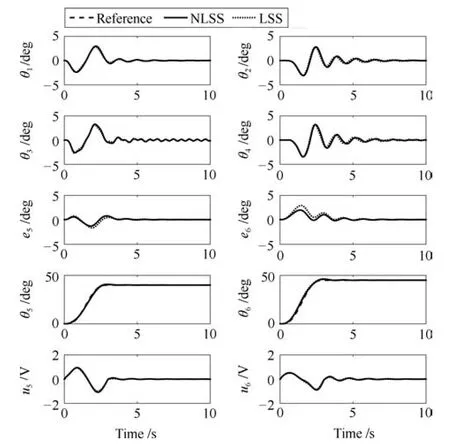
图3 仿真结果(l2=0.1m)Fig.3 Simulation results(l2=0.1m)

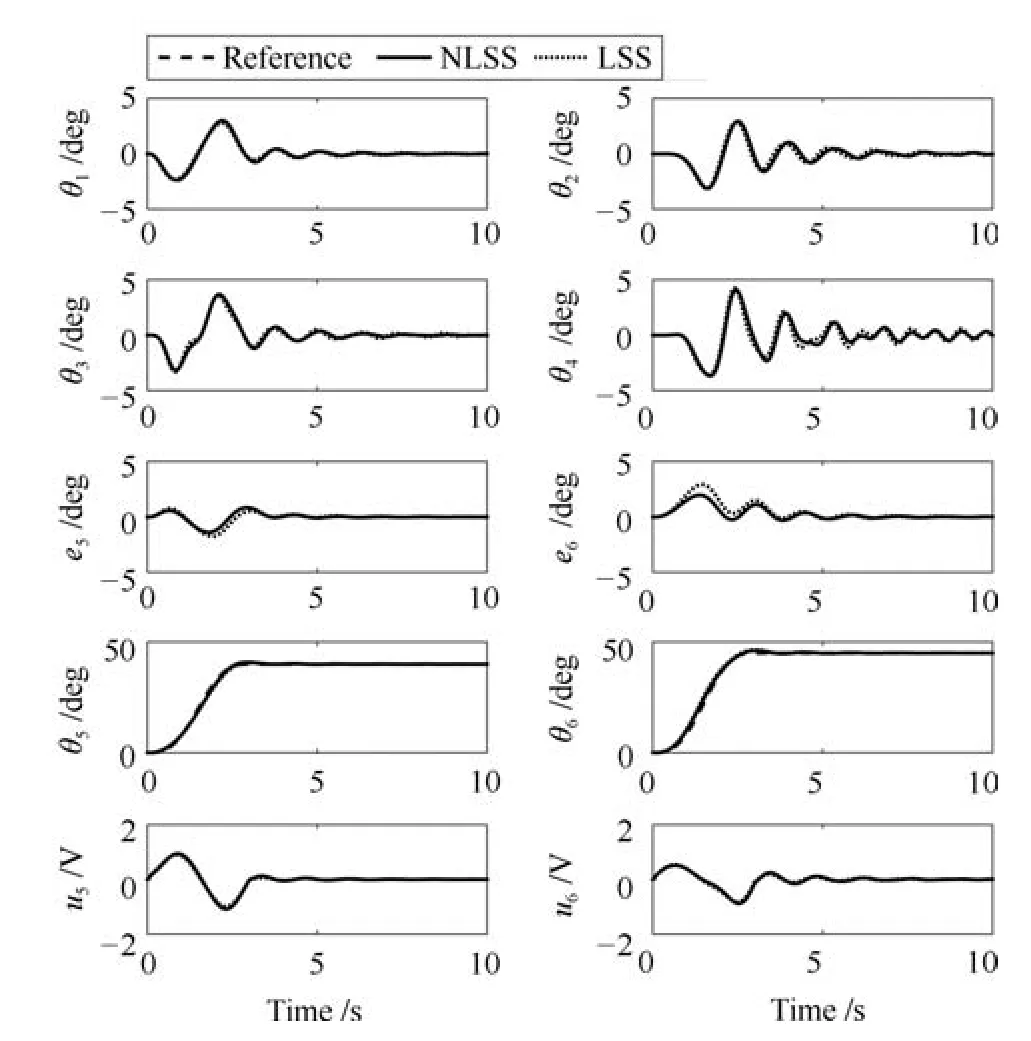
图4 仿真结果(l2=0.2m)Fig.4 Simulation results(l2=0.2m)

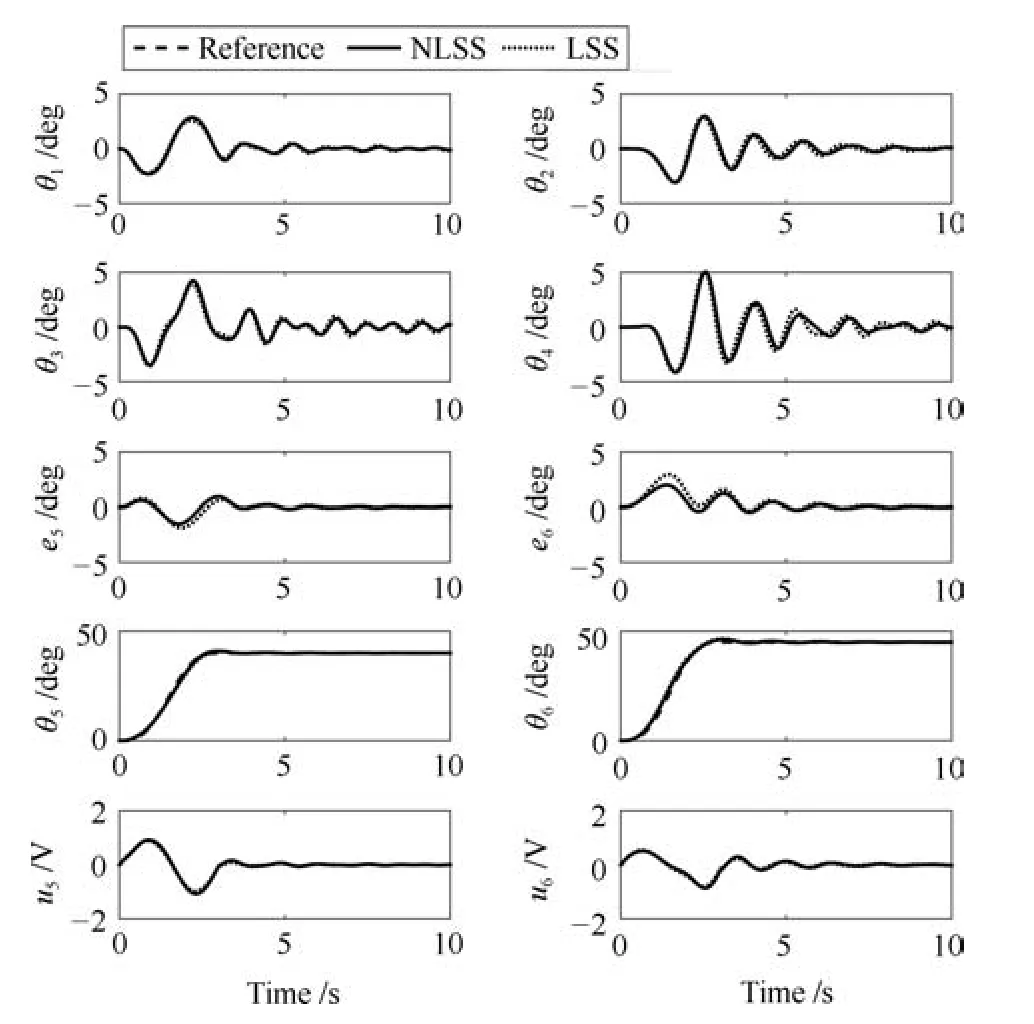
图5 仿真结果(l2=0.3m)Fig.5 Simulation results(l2=0.3m)

为了进行定量分析,分别将本文所提方法和传统方法应用于旋转起重机时的最大起伏角误差e5max(deg),最大旋转角误差e6max(deg),起伏方向第一级摆角最大值θ1max(deg),起伏方向第二级摆角最大值θ3max(deg),旋转方向第一级摆角最大值θ2max(deg)和旋转方向第二级摆角最大值θ4max(deg)如表4∼表6所示.由这些图与表可知,虽然两种方法对于悬绳长度变化都具有鲁棒性,但是使用本文所提方法可以分别减小大约40%的起伏角最大跟踪误差和52%的旋转角最大跟踪误差.另外,对于所有的情况,荷载摆动都得到了良好的抑制,并且随着悬绳长度的增加摆角也逐渐增大.这些结果验证了本文所提方法既具有较好的鲁棒性还具有较好的跟踪性能,同时不降低摆角抑制性能.

4 结论

本文为了同时实现双摆旋转起重机高精度跟踪和摆角抑制,首先,建立含有双摆效应的起重机动力学模型,并采用干扰观测器进行解耦线性化.其次,基于此线性模型分别为其设计含有非线性滑模面的滑模控制器,并通过李雅普诺夫定理分析其稳定性.通过采用本文所提方法,无论吊绳长度l2=0.1m,l2=0.2m或者l2=0.3m,都实现了旋臂起伏角和旋转角的跟踪和两级残留摆角的抑制.通过与传统线性滑模比较,在不改变控制器摆角抑制性能的前提下,起伏角和旋转角的跟踪误差分别降低了大约40%和52%.

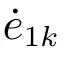
附录A 不同非线性滑模面参数对控制性能影响分析

本节通过仿真对非线性滑模面参数选取进行分析,并获得其对控制性能的影响.在图A示的结果中,实线对应参数表2中λik值,点线分别对应λ11=12,λ21=15,λ31=7,λ12=12,λ22=15和λ32=8.而点划线则对应λ11=120,λ21=150,λ31=70,λ12=120,λ22=150 和λ32=80.由图可知,虽然随着λik的增大,旋臂的定位精度会大大提高,但是同时也降低摆角抑制性能.

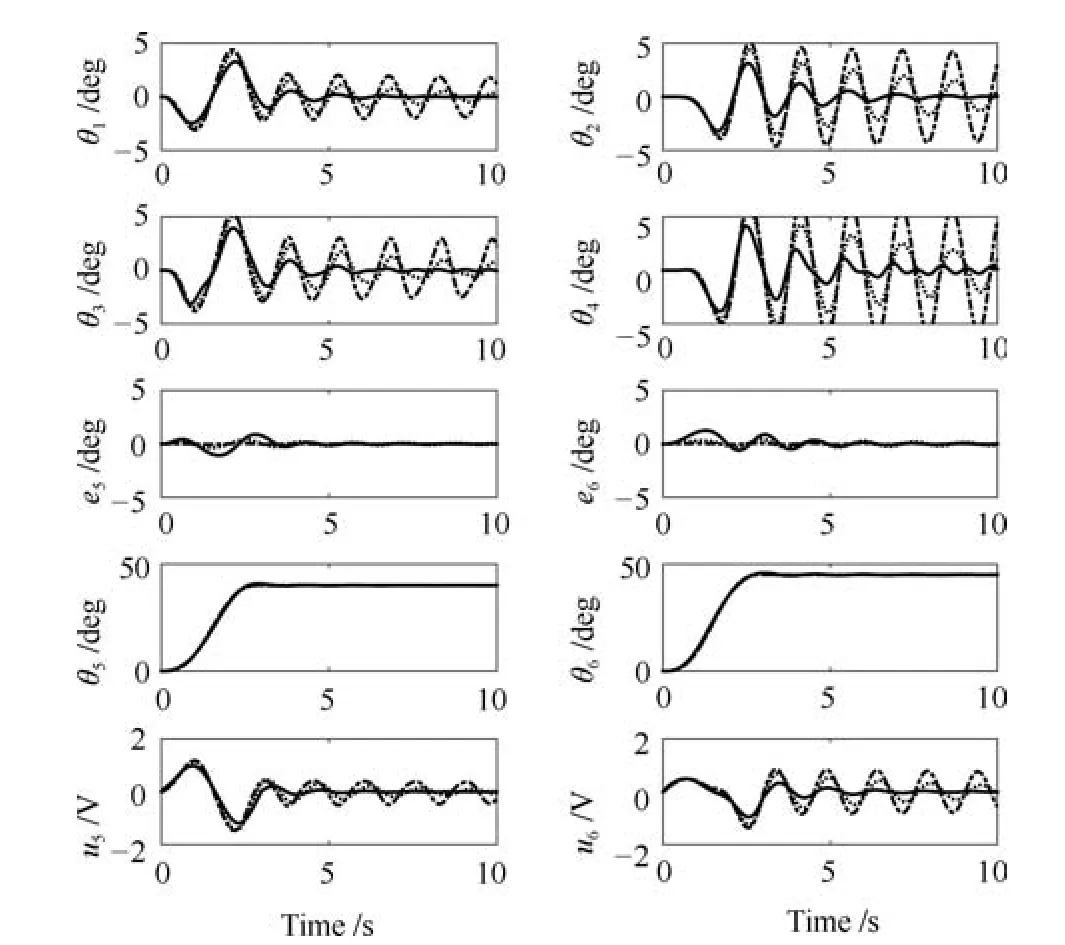
图A1 不同λik情况下的仿真结果Fig.A1 Simulation results for different λik