PBL主题拓展教学：完善学生数学思维结构的一种有效路径

一、释义：PBL主题拓展教学的内涵诠释

PBL是Problem－Based Learning的缩写，是指基于问题的学习。PBL主题拓展教学是指根据学生的年龄特征和认知经验，围绕有价值的教学主题，由教师精心设计问题或师生合作提出问题，并通过超级链接不断拓展相关联的未知领域，开阔学生的视野，使他们形成新见解。这一过程能充分调动学生的认知能力和思维能力，有助于学生把分散的、零碎的知识点统整起来，从而使他们的思维结构更加完善。PBL主题拓展教学有五大特性：

第一，主题的种子性。主题是种子，它的确立基本上决定了PBL主题拓展的深度和广度，因而应依据学生的认知水平和生活经验来确定，应凸显其丰富的内涵和核心价值。

第二，问题的驱动性。美国教育家尼尔·博斯特曼说：“一旦你学会了提问，掌握了提出有意义的、恰当的和实质性的问题的方法，你就掌握了学习的技巧。”PBL主题拓展教学以一个或多个问题的解决为驱动力，促进学生主动参与学习，使问题真正成为他们研究和探索的出发点和归宿。

第三，活动的互动性。PBL主题拓展教学关注学生的全身心投入，主张为学生提供广阔的合作探究空间和必要的“脚手架”，并在问题解决的关键处给予点拨和引领，帮助学生在研究中提升能力、积累经验，最终寻得解决问题的方法。

第四，内容的系统性。荷兰教育家弗赖登塔尔说：“数学是系统化了的常识。”PBL主题拓展教学引导学生以主题为载体进行超级链接，将相关联的内容串成链、织成网、结成块、聚成球，由点到线、由线到面、由面到体地编织自己的数学系统和经验系统，不断形成自己系统化的数学思考和观点。

第五，思维的延展性。德国数学家康托尔说：“数学的本质是自由的。”学生的思维在自由的状态下才能自由地生长。以PBL主题拓展教学为中心进行思维的延展，可以是线性延展形成思维通道，可以是圆形延展形成结构化思考，也可以是球形发散形成立体化生长。

二、探源：PBL主题拓展教学的价值建构

教学观念的全面开放。PBL主题拓展教学以问题驱动，以主题将课内外、各学科零散的、单一的素材统整起来，逐步构成“集成块”；将与主题相关联的知识进行超级链接、精细加工，并对其进行深度挖掘与深入理解，促进学生举一反三、触类旁通。

学习方式的全景融合。PBL主题拓展教学不但对教学内容进行系统化的融合与补充，还改变了课堂教学的面貌，呈现出开放与自由的特点。在PBL主题拓展教学中，课内外都成了学生研究与学习的场所，促使他们用数学的眼光去发现和研究课堂之外的数学问题，用课内学到的数学知识去解释生活中的现象。

思维认知的全息编码。PBL主题拓展教学的核心是发展学生的思维。它从主题出发，以问题节点为脉络主动发散，形成纵横交错、有机互补的新主题，随着一个个不同主题的拓展，每个主题之间又生长出新的问题节点，从而不断补充学生原有的结构体系，逐步完善学生的认知结构和思维结构。

三、寻绎：PBL主题拓展教学的智性实践

（一）构建PBL主题拓展教学的问题情境场域，激活学生数学思维的外部环境

1.找准核心问题，激发学生思维的内部需求。

核心问题是一节课中最重要的问题，它可以是一个或几个，可以是教师精心设计或师生合作共同提出的。在教学时，可以通过核心问题推进教学过程不断聚焦生成，激活学生个体不同的内在思维，再通过多维互动使拓展生成的资源围绕主题逐渐条理化，从而使学生的思维结构更具丰富性、具体性、开放性。如教学苏教版六上“长方体和正方体”后，可以设计PBL主题拓展课《一张白纸中的数学》：

教师引导学生提问：就这张白纸而言，从数学的角度，你可以提出哪些问题？

学生提出问题如下：这张白纸的周长是多少？重量是多少？长和宽的比是多少？厚度是多少？它能写多少个字？把它做成长方体或正方体，容积是多少？……

师生合作梳理问题。这张白纸本身的问题有：长、宽、周长、面积、体积、厚度、重量、表面积……在生活中的问题有：它的成本是多少？它能写多少个字？……在数学上的问题有：在它上面画最大圆，面积是多少？把它折成长正方体，容积是多少？……

教师以“提出关于一张白纸的数学问题”为该课的核心任务，立刻激活了学生对一张白纸的生活和学习经验，使他们提出了很多问题。教师及时引导学生对这些问题进行梳理与分类，从而整理出白纸本身及其在生活中和数学上存在的三类问题，促使学生生成的问题资源条理化。这样，既尊重学生的内在需求，又生成了课堂学习的焦点，彻底激活了学生系统化探究知识的内在需求。

2.聚焦主题脉络，搭建学生思维的立体平台。

PBL主题拓展教学以主题为核心建构教学的主干脉络，一节课可以围绕一个主题，由几个不同形式的活动模块组成，使学生在丰富多彩的活动中自主、合作学习，体验、感悟和探究主题内容，展示、交流和分享学习成果，从而完善思维结构。如教学苏教版六下“圆锥的体积”后，可以结合课后习题设计PBL主题拓展课《探索三角板的奥秘》：

提问：可以研究三角板的哪些方面？

模块一：研究三角板的角。利用三角板的角能画出多少度的角？你能发现什么规律？

模块二：研究三角板的边。三角板的斜边与直角边或斜边上的高有关系吗？有怎样的关系？怎样证明？

模块三：研究两块三角板的联系。两块三角板之间有怎样的联系就能确定它们是一对三角板？

模块四：将两块一样的三角板的两条相同边重合拼在一起，能拼出几种不同的四边形？

模块五：将一块三角板沿其中一条边进行旋转，能形成什么图形？怎样旋转形成的图形体积最大？

教师聚焦学生熟悉的三角板，深度挖掘它的角、边、面、配对奥秘等有趣的数学元素，激活学生头脑中的关联思维，为学生参与课堂教学活动搭建立体平台，并充分利用各种平台完善学生的思维结构。

（二）构建PBL主题拓展教学的探究发生场域，催生学生数学思维的动力机制

1.探究路径多元化，拓宽学生思维的视域。

在PBL主题拓展教学中，面对学生认知和能力“最近发展区”的问题，教师注重引导学生从不同的角度、用不同的思维方式对问题进行探究；强调通过小组讨论和全班交流，使学生共享问题探究方法的多元路径，不断拓宽学生思维的视域。如教学苏教版四下“三角形、平行四边形和梯形”后，可以设计PBL主题拓展课《图形中的规律》：

问题：像这样围100个正方形，需要多少根小棒？

化大为小：从围2个正方形开始研究，围2个正方形需要的小棒根数用算式怎样表示？并说说算式的含义。

回顾：要知道围2个正方形需要的小棒根数，可以正着想——起点4根多3，起点1根多3多3，也可以反着想——从总根数中去掉重叠的1根。（如图1）

（图1）

多维度探究：选择一种研究方向，合作探究围100个正方形需要的小棒根数。

教师引导学生化大为小，先从围2个正方形开始探究，学生借助直观材料动手操作，并在分享中获取多元路径的探索方法，接着自主选择一种方法进行有序探究，找出规律后顺利解决问题。学生在基于实践的多元路径的数学活动中进行深度探究，在一定程度上拓宽了思维的视域。

2.探究过程高效化，提升学生思维的经验。

在PBL主题拓展教学中，学生是探究的主体，教师将主动权还给学生，但学生由于其自身能力和经验的不足，有时花费很多时间仍探究不出头绪，抑或探究仍处于浅层水平。因而教师要在学生遇到困难时及时给予点拨，在关键处及时进行引领，帮助学生进行自主化且高效化的数学探究，不断提升学生思维的经验。如教学苏教版六下“圆柱的体积”后，可以设计PBL主题拓展课《巧算圆柱体积》：

问题：用两张同样大的长方形纸卷成圆柱体，怎样卷体积比较大？

学生探究：赋值法，假设长 18.84（6π），宽6.28（2π），计算得出沿长边卷和沿短边卷形成的圆柱的体积分别为18π2和6π2，所以沿长边卷体积大。

教师点拨：回顾圆柱体积推导过程，除了可以用底面积乘高的方法计算体积，能否找出别的方法？

推导：如图2所示，倒下后的近似长方体的底面积是圆柱侧面积的一半，高是圆柱的半径，所以，圆柱的体积＝侧面积的一半×半径。

（图2）

运用结论：用同样大的两张纸卷成圆柱，侧面积相等，侧面积的一半就相等，而沿长边卷的圆柱半径长，所以沿长边卷体积大。

学生基于经验用常规方法“底面积×高”分别计算出了两个圆柱的体积，结果正确但计算过程比较烦琐。在教师的引导和点拨下，他们接着探究出圆柱体积计算的另一种方法——“圆柱侧面积的一半乘半径”，很容易就解决了较复杂的数学问题。

（三）构建PBL主题拓展多元建构场域，实现学生数学思维的融通跨越

1.纵向拉伸，实现思维由浅入深的建构。

纵向拉伸就是将单元内、单元间甚至跨年级的同类知识内容，按其内在的逻辑关系由简单到复杂地串成一个知识结构链，使学生对知识间的纵向关联有清晰的认知与把握，并在头脑中构建起更加精致的知识框架。如教学苏教版五上“公顷和平方千米”后，可以结合课后习题进行如下PBL主题拓展教学：

习题：按从小到大的顺序说说已经学过的面积单位，并说说两个相邻单位之间的进率。

学生自主整理形成表格，并生成核心问题：为什么公顷和平方米之间的进率是10000，而两个相邻面积单位之间的进率是100？

超链接：边长为10米的正方形的面积是1公亩。

学生自主建构面积单位线性图（如图3）：

（图3）

教师站在整体、系统的高度把握、审视和智慧地处理教材，引导学生自主生成核心问题，并不断拓展与面积单位相关联的领域，帮助学生根据知识点的衔接关系在头脑中形成了一套完整的知识体系，发展并完善了学生的认知系统和数学思维。

2.横向贯通，实现思维由此及彼的勾连。

横向贯通就是把与某一知识点具有内在同类特征的相关内容整合成一个知识整体，重在突出知识结构间的横向关联性，丰富学生对类结构特征知识内涵的认识和把握，提升学生分类、比较、概括、抽象的能力，从而实现其数学思维由此及彼的勾连。如教学苏教版五上“平行四边形的面积”时，可以设计如下PBL主题拓展教学：

回顾：同学们学习过哪些图形的面积计算方法？它们的计算方法有什么共同之处？

聚焦：长（正）方形的面积＝每行单位面积个数×行数。

提问：能用这个公式求平行四边形的面积吗？学生操作形成如下图4所示的新图式：

（图4）

联系：每行单位面积个数是平行四边形的底，行数是平行四边形的高，所以，平行四边形的面积＝每行单位面积个数×行数＝底×高。

拓展：用这种研究方法研究其他图形的面积。

常规教学重视面积计算公式的获得与应用，却常常忽略度量本质的体现。因此，教师设计上述PBL主题拓展教学，先让学生初步感受二维图形的面积是由每行单位面积的个数和行数这两个维度的量相乘得出的，再让学生用方格纸上的单位面积度量平行四边形，不但继续渗透度量的本质，更以平行四边形为纽带，横向贯通平面图形面积的计算方法——“每行单位面积个数×行数”，建构其背后共通的思维方式。

3.纵横融通，实现思维由内而外的生长。

纵横融通既要关注知识间的纵向拉伸，又要关注知识间的横向贯通，还要打破横向和纵向知识的界限，超越原有单元和年段的界限，把视野拓展到整个年级甚至各学段的教学中，形成主次分明、有机渗透、纵横交织的知识网络，实现数学思维由内而外的生长。如教学苏教版五上“多边形的面积”单元后，可以结合复习内容开展如下PBL主题拓展教学：

提问：我们已经学习了六种平面图形，它们都有各自的面积公式，你能用其中一种图形的面积公式代表其他五种图形的面积公式吗？

链接（如图5）：长方形和平行四边形可以看作上底和下底是a的梯形；正方形可以看作上底、下底和高是a的梯形；三角形可以看成上底是0的梯形，因而梯形的面积公式可以代表其他五种图形的面积公式。

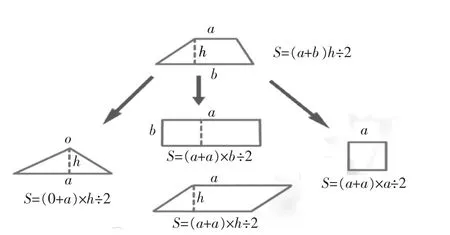
（图5）

教师打破传统的结网模式，在转化六种平面图形的面积公式上下功夫，学生只要掌握梯形的面积公式，便能顺藤摸瓜得出其他五种平面图形的面积公式，这样的知识网络更有利于学生迅速提取和应用，使学生体验到归纳推理和演绎推理的独特价值，真正实现知识之间的自然贯通与数学思维的多维生长。

总之，PBL主题拓展教学有助于改进学生的学习方式，充分发展学生的智慧品质，又能让学生在活动过程中不断完善思维结构。

注：本文获2018年江苏省“教海探航”征文竞赛一等奖，有删改。