初中数学单元教学目标制订研究*
——基于布卢姆教育目标分类学原理
一、教学目标制订中的问题
目前,备课组的教研活动一般以集体备课形式开展,经过研讨后以个人为主编写课时教案(学案)。但是,在集体备课时存在一个比较普遍的问题,就是很少集体研究并制订每个单元的教学目标。即使有时对其进行了研究,但仍存在目标如何制订、如何表达、如何实现、目标达成如何检测等问题。笔者以为,布卢姆教育目标分类学的相关原理能为初中数学单元教学目标的制订提供借鉴。
二、布卢姆教育目标分类学概述
1956年,美国教育心理学家布卢姆主编了《教育目标分类学·第一分册:认知领域》(以下简称《手册》),《手册》面世60多年来,已经被翻译成20多种文字。不仅在美国,而且在全世界,为测验设计和课程开发提供了基本的依据。1995-1999年,洛林·W.安德森等修订了《手册》。[1]
(一)布卢姆的知识维度连续体
布卢姆将知识分为四类:事实性知识、概念性知识、程序性知识、元认知知识,它们在知识维度上构成了一个连续体。
A.事实性知识:包括学科专家用于学术交流以及系统地组织学科的基本要素。
AA.术语知识:包括关于言语和非言语的特殊标记和符号,是该学科的基本语言。如:+、-、×、÷、⊥、∥、、∽、△、∵、∴、∠、≧、︵、⊙等等。
AB.具体细节和要素知识:包括事件、地点、人物、日期、信息源等知识。例如:祖冲之第一个把圆周率准确算到小数点后第7位,π≈3.1415926。
B.概念性知识:包括关于分类和类别以及它们之间的关系的知识,是更为复杂的、结构化的知识形态。
BA.分类和类别知识:包括用于不同学科的具体类别、组别、部类和排列。例如:整数和分数都可以归入有理数类别。
BB.原理和通则的知识:原理和通则往往是学生难以理解的一般性思想和概念。它们被用来研究该学科的现象或解决问题。例如:勾股定理,等腰三角形的两个底角相等,单项式的概念,乘法交换律,等等。
BC.理论、模型和结构的知识:包括原理和通则及其相互关系的知识。他们为复杂的现象、问题或一个学科提供清晰全面系统的见解。例如:函数模型、不完全归纳理论、几何方法、数形结合方法、极端思想等等。
C.程序性知识:程序性知识是关于如何做某事的知识。
CA.具体学科的技能和算法的知识:程序性知识可以表示为一系列或序列步骤,这些步骤被统称为一个程序。例如:一元一次方程的解法,不等式的解法,单项式乘多项式法则,有理数的加减乘除运算,等等。
CB.具体学科的技术和方法的知识:这类知识并不能导致一个预先确定的答案和解决方案,结果更为开放和不确定。例如:转化法、待定系数法、换元法、加减消元法、代入消元法。
CC.确定何时使用适当程序准则的知识:除了懂得具体学科的程序之外,学生还需要知道何时使用这些程序,这涉及了解这些程序以往的使用方法。例如:分式转化为整式时要去分母,根式转化为有理式或者遇到绝对值号时要想到用平方法,遇到两个中点构造中位线时要用构造法,遇到求最值时要想到函数模型,遇到高次要想到换元降次,等等。
D.元认知知识:元认知知识是关于自我认知的意识和知识。
DA.策略性知识:策略性知识是关于学习、思维和解决问题的一般性策略的知识。这些策略能够用于许多不同的任务和学科,而不是只针对某一学科领域中的某一类任务。
DB.关于认知任务的知识:除了关于各种策略的知识,个体还积累了关于认知任务的知识。例如:知道回忆题比识别题更加困难。
DC.关于自我的知识:①包括对自己在认知和学习方面的弱项强项的了解;②对自己知识基础的广度和深度的自我认识;③学生需要意识到在不同的情境中,自己可能需要的各种一般策略。
(二)布卢姆的认知过程维度连续体
布卢姆提出了从记忆到创造六个类别的认知过程连续体,共19种具体的认知过程,每个认知过程都有同义词,笔者依据自己的理解按照初中数学学科分别举例说明,见下页表1。
(三)布卢姆认知目标分类二维框架
布卢姆在一个认知目标(单元教学目标)的陈述中,包含一个动词和一个名词,动词通常描述预期的认知过程,名词通常描述希望学生将要习得或建构的知识。此外,布卢姆将教育目标用认知目标分类二维框架[2]来集中表达,例如“教育目标:学生将学会区别(认知过程)有理数和无理数(知识)”中,“区别”属于“4.分析”认知过程,“有理数和无理数”属于概念性知识,于是这样一个目标就用“B4”来表示,如表2所示。
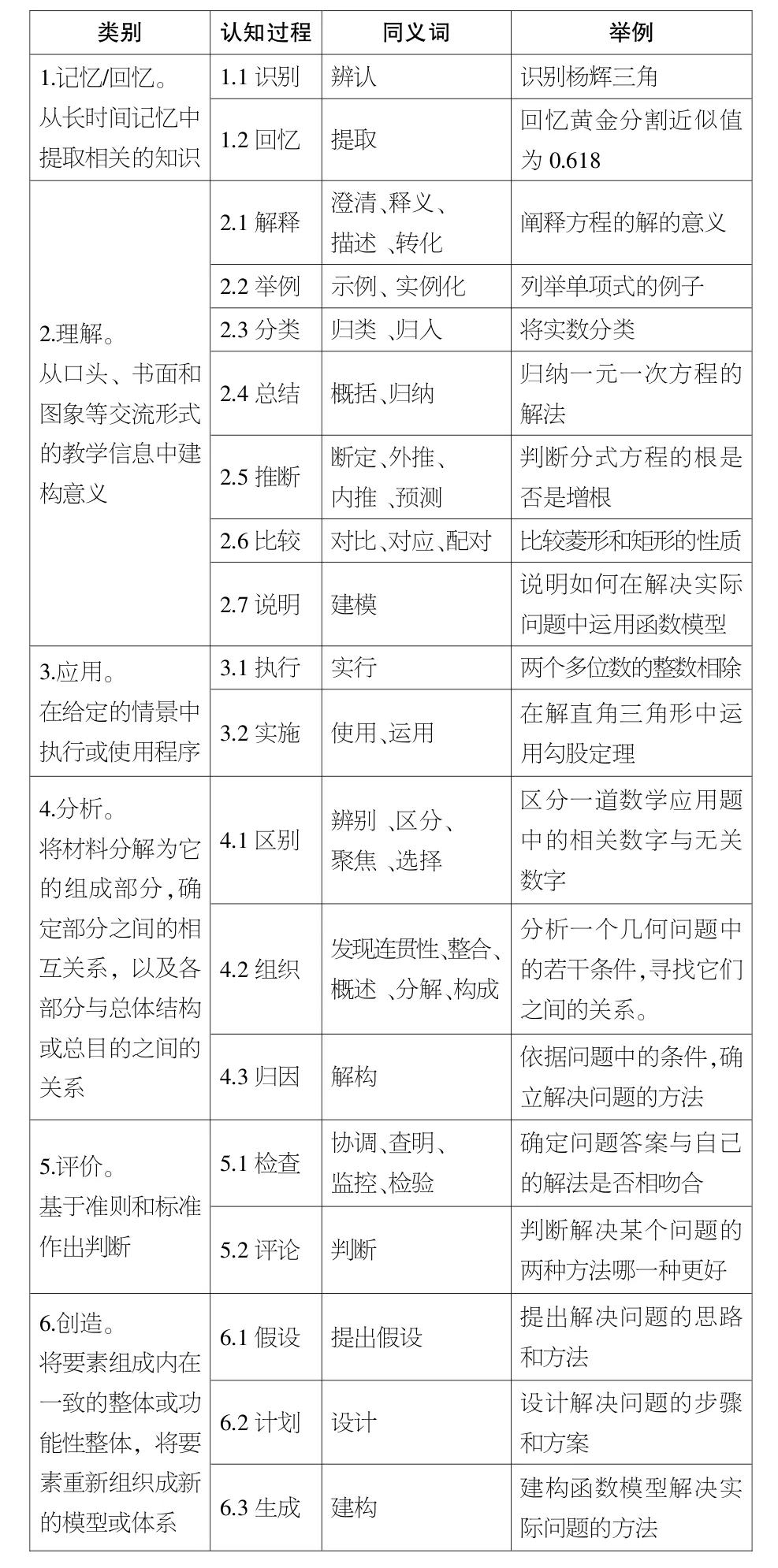
表1 认知过程维度及举例
三、“一次函数”单元教学目标的转换与拓展
我们基于苏科版初中数学配套教师用书[3],对教材八上第六章“一次函数”的单元教学目标进行转换和拓展,并用二维框架集中表达(见下页表3)。
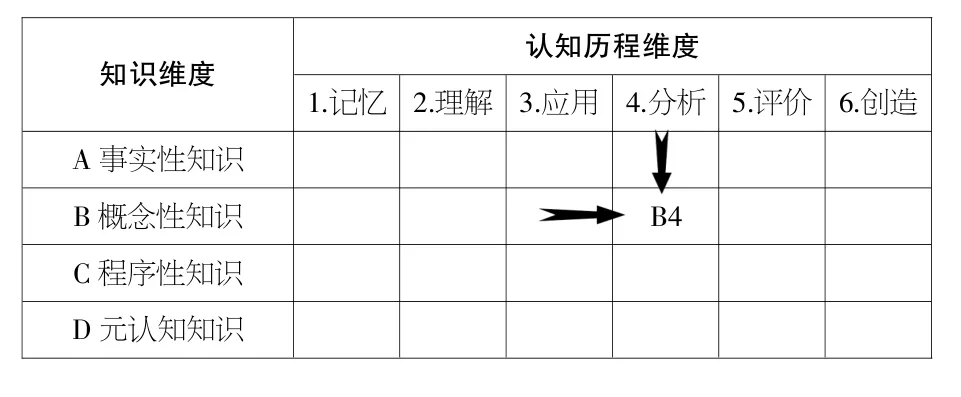
表2 认知目标二维分类表
1.“一次函数”单元教学目标的转换。
(1)通过简单实例,了解常量、变量的意义。
目标1=B2=解释概念性知识=学生能够阐释常量和变量的意义。
(2)能结合实例,了解函数的概念和三种表示方法,能举出函数的实例。
目标2=B2=举例概念性知识=学生能够举出函数的实例。
(3)能用适当的方法刻画某些实际问题中的函数关系,并能结合图象对函数关系进行分析。
目标3=C3=实施程序性知识=学生能够选择适当的方法刻画实际问题中的函数关系。
目标4=B2=推断概念性知识=学生能够结合图象分析函数关系。
(4)能确定简单的整式、分式和简单实际问题中函数的自变量取值范围,会求出函数值。
目标5=C3=执行程序性知识=学生能够确定整式、分式和实际问题中自变量取值范围。
目标6=C3=实施程序性知识=学生能够通过代入自变量的值求函数值。
(5)结合具体情境体会一次函数和正比例函数的意义,根据已知条件确定一次函数关系式。
目标7=B2=解释概念性知识=学生能够描述一次函数和正比例函数的概念。
目标8=C3=实施程序性知识=学生能够根据依据条件确定一次函数的关系式。
(6)会画一次函数的图象,能根据一次函数的图象和点的关系式,探索并理解其性质。
目标9=C3=执行程序性知识=学生能够画一次函数的图象。
目标10=B2=总结概念性知识=学生探索、归纳并理解一次函数的性质。
(7)会用一次函数的图象,求二元一次方程组的近似解。
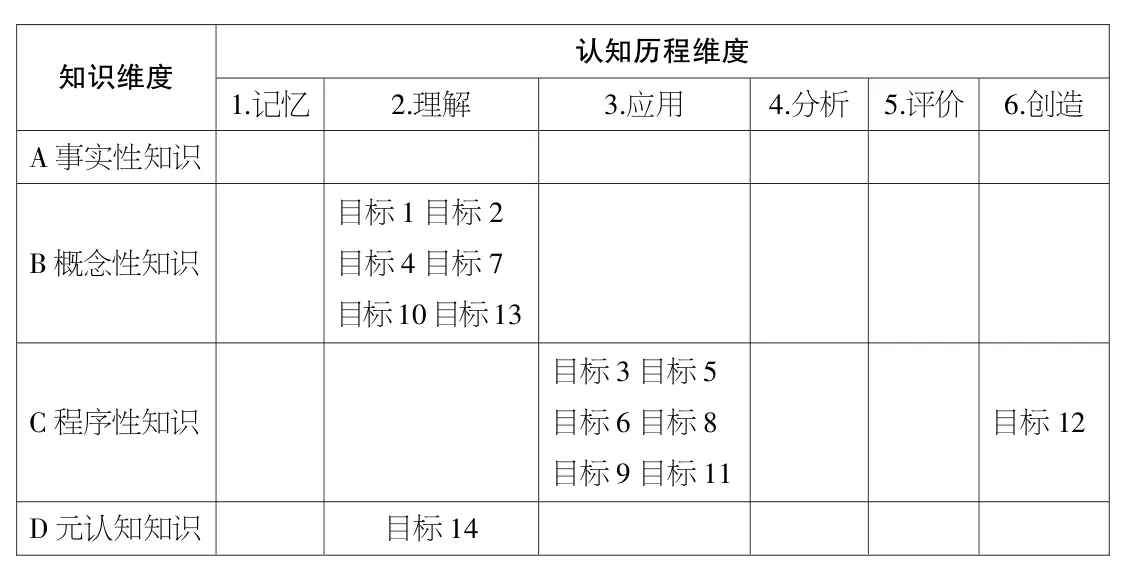
表3 “一次函数”单元教学知识目标二维分类表
目标11=C3=执行程序性知识=会用一次函数的图象,求二元一次方程组的近似解。
(8)能用一次函数解决实际问题,会结合对函数关系的分析,尝试对变量的变化规律进行初步的预测。
目标12=C6=生成程序性知识=学生能够运用一次函数解决实际问题。
目标13=B2=推断概念性知识=学生能结合对函数关系的分析,对变量的变化规律进行预测。
(9)通过实验观察探索等活动,感受函数是研究现实世界数量关系及变化规律的重要数学模型,体验函数是处理和解决实际问题的有力工具并具有广泛应用性,逐步深化对函数思想的理解。
目标14=D2=解释元认知知识=学生能够理解函数是解决有关数量关系问题的模型。
2.“一次函数”单元教学目标的拓展。
在初中阶段,依据学生的认知规律,分别设计了不同年级的数学单元内容,各单元知识内容既有独立性又有一定的交叉性,单元内容落实单元目标,单元目标的落实逐渐培养学生的学科核心素养。对上述“一次函数”单元目标从数学核心素养的角度进行扩展,可以得到如下分类——
数学抽象:目标2、目标7、目标9、目标14。
逻辑推理:目标 2、目标3、目标4、目标8、目标 10、目标12、目标14。
数学建模:目标3、目标8、目标9、目标12、目标14。
直观想象:目标4、目标9。
数学运算:目标6、目标8、目标11。
数据分析:目标1、目标5、目标11、目标13。
从整体数学知识框架来看,“一次函数”这一章节在初中教育阶段的重点是培养学生的数学抽象、逻辑推理、数学建模素养。教师在教学中,可以按照教学内容依次达成单元设计中的各个目标,在目标探索和达成过程中,潜移默化地培养学生相应的数学素养,从而保证学生学习生涯中核心素养培养的持续性。

