基于传递特性的航天器在轨冲击环境预示方法研究

李会娜，高 庆，卢 鑫，秦朝红

（1. 北京强度环境研究所； 2. 中国运载火箭技术研究院：北京 100076）

0 引言

航天器在发射和飞行期间会承受由于起飞、分离、关机和入轨等各种时序动作引起的噪声、振动、冲击等动力学环境[1]。NASA的统计数据表明：高频冲击环境是导致飞行故障的主要环境因素，对飞行任务有着重要影响[2]。NASA自20世纪70、80年代开始深入研究火工冲击产生和传递的机理、冲击响应的预示方法及试验模拟技术，并制定相应标准[3]，以规范火工冲击相关的试验、设计和预示方法，有效控制火工冲击导致的飞行故障。

冲击环境具有以高频为主的宽频带、瞬态和强非线性的特点，因此很难利用分析方法准确预示结构的冲击响应。目前各环境设计和试验标准主要采用经验模型、数据外推、子结构路径外推等统计类预示方法[3]，也有学者利用 LS-Dyna、Hydrocodes、统计能量法、虚模态综合法等数值分析方法，预示结构的高频冲击响应[4-6]。统计类预示方法通常得到的是冲击环境的包络值，预示速度快但误差较大；数值类预示方法通常对冲击环境的预示较为精确，但很难考虑冲击源和结构传递等偏差的影响，并且计算规模大、耗时长。在实际工程中，经常遇到已知结构某处的冲击环境，需要较为精确地确定其他部位的冲击环境及其分布情况，此时统计类方法和数值类方法都不太适用。

本文参考结构传递函数的定义和性质，建立了2种基于传递特性的冲击环境预示方法，可在已知结构某处的冲击环境以及两部位间传递特性的基础上，较精确地得到指定部位的冲击环境及其分布，并利用冲击试验测量结果进行了预示结果的验证。旨在为航天器冲击环境的统计分析、环境条件制定、地面试验设计以及相关故障分析等提供参考。

1 冲击环境传递特性分析方法

1.1 基于时域数据的传递函数

传递函数可以描述系统的动力学特性，反映结构系统中两点之间的传递关系。对于线性系统而言，其传递关系主要取决于系统的刚度、质量以及阻尼等特性，与外界激励无关[7]。因此，可利用火工品分离试验测量得到的冲击时域数据，获得两结构部位之间的传递函数，以描述两点之间的传递关系；并利用多次试验的测量分析结果，改进和完善传递函数的分析精度。x点和y点之间的传递函数为

式中：Sxx(ω)为x点的自谱密度；Sxy(ω)为x点和y点的互谱密度；Gi(ω), (i=x/y)为x点/y点的傅里叶变换。

可利用相干函数评定传递函数估计值的优劣，传递函数估计较好时，其对应的相干函数

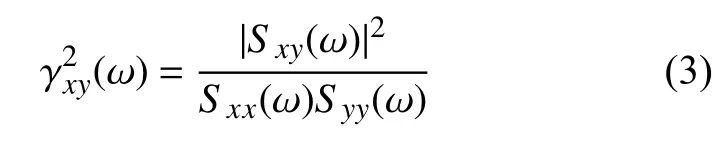
应当接近1。

1.2 基于冲击响应谱的传递关系

冲击响应谱为单自由度系统在基础冲击激励作用下的最大响应。设单自由度系统的固有频率为ωn，阻尼比为ζ，则有：

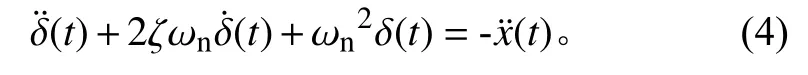
当阻尼比ζ＜1，且单自由度系统初始位移和初始速度为0时，系统加速度响应为

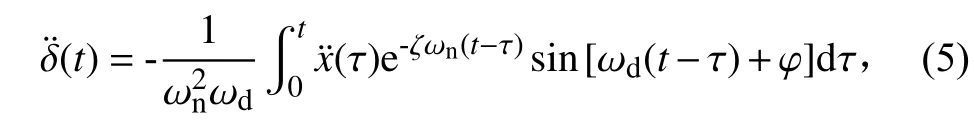
其中ωd为有阻尼系统的振动频率（自然频率）；

固有频率ωn处的加速度冲击响应谱为

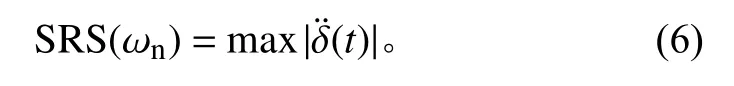
大部分情况下，历史冲击试验数据仅保留冲击响应谱数据，无法使用传递函数描述系统的传递特性；但可利用各测点的冲击响应谱分析结果，粗略描述系统的传递特性。

可参考传递函数的定义，将冲击响应谱的传递关系定义为

由于冲击响应谱分析过程中丢失了信号的相位关系信息，所以式(7)定义的冲击传递关系不是传递函数，不能描述两信号的相位传递特性，仅为表示两信号的冲击响应谱幅值比例系数的标量。

2 基于传递特性的冲击环境预示方法

在实际航天工程中，由于冲击测量的限制条件较多，通常利用地面试验较为全面地测量产品的冲击环境；而在飞行试验中，仅测量少量部位的冲击环境。因此，常常需要由已知部位的冲击环境，外推其他部位的冲击环境。一般存在2种情况：1）已知输入点的时域数据和两点间的传递函数，预示输出点的冲击环境；2）已知输入点的冲击响应谱和两点间的冲击响应谱传递函数，预示输出点的冲击环境。

2.1 基于时域数据和传递函数的预示方法

根据传递函数的定义，已知输入点的时域数据和两点间的传递函数，可得到输出点的时域数据，计算公式为

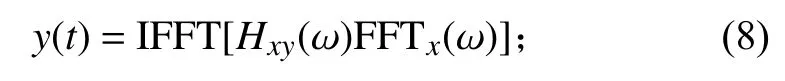
然后采用改进的数字滤波方法对输出点的时域数据进行处理，即可得到该点的冲击环境。

2.2 基于冲击响应谱及其传递关系的预示方法

根据冲击响应谱传递函数的定义，可直接利用已知输入点的冲击响应谱及两点间的冲击传递关系，得到输出点的冲击环境，即

3 基于传递特性的冲击环境预示及验证

在某火工品分离试验中，测量得到了多处部位的冲击环境，其中相同部位相同方向的有效冲击数据为5组，可用于检验上述2种冲击环境预示方法。试验中测量得到的某两点的5次冲击响应谱如图1所示。

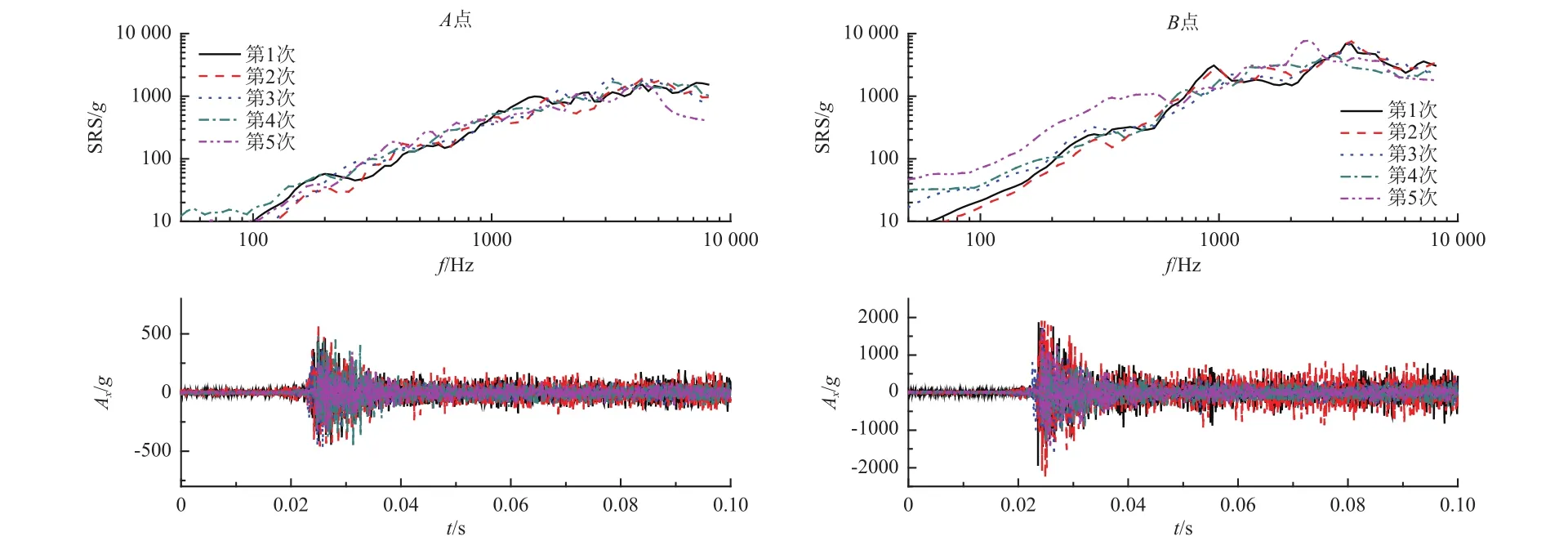
图1 某两点的5次时域和冲击响应谱测量数据Fig.1 The time domain and shock response spectrum data of two points for five times

假设A为输入点、B为输出点，B点的第5次冲击环境未知，利用前4次A点、B点的冲击响应数据，可分析得到A、B两点之间的冲击传递特性；然后分别采用上述2种方法，根据A点的第5次响应数据及两点间的传递特性，预示B点的第5次冲击响应谱（SRS），并与实测数据的SRS分析结果进行对比（见图2），以验证2种方法的优劣和可用性。

图2 输出点的冲击响应谱测量结果及预示结果对比Fig.2 Comparison between measured and predicted results of shock response spectrum for the output point

由图2可见，2种预示方法中，时域数据+传递函数法和SRS传递方法的预示结果均与原试验测量分析结果基本吻合，规律一致，全频带误差小于±9 dB，大部分频段误差小于±3 dB。同时可以看到，各预示方法的误差大小主要取决于用来获得传递函数的冲击测量数据的散布情况，散布越大，误差就越大。

4 结论和建议

本文参考结构传递函数的定义和性质，建立了2种基于传递特性的冲击环境预示方法，在已知结构某处的冲击环境以及两部位间传递特性的基础上，可较精确地得到其他指定部位的冲击环境及其分布，并利用某冲击试验测量结果对该方法进行验证，得到以下结论和建议：

1）2种基于传递特性的冲击环境快速预示方法均能够得到较为精确的冲击环境预示，量级和变化规律一致，其中以SRS传递方法的精度最好，大部分频率误差小于±3 dB；

2）基于传递特性的冲击环境快速预示方法的预示精度与冲击数据的积累、散布情况、结构相似程度等相关，建议搜集积累更多分离冲击环境数据，为相似分离方案的冲击环境预示、扩展地面及飞行试验结果的使用范围、剥离异常冲击测量结果等提供参考。