空间站舱外泄漏羽流场数值模拟

花 雨，毕海林，孙 伟，孙立臣，孟冬辉，王旭迪*

（1. 合肥工业大学 机械工程学院，合肥 230041； 2. 北京卫星环境工程研究所，北京 100094）

0 引言

载人航天器在轨运行中受到各种外部因素的影响，若密封性遭到破坏，会使其内部压力发生变化，危害航天员的生命安全。因此，有必要对舱内气体外泄过程进行研究，找到快速定位漏孔，测量漏率，判断风险的有效方法。

目前国内对于空间站外部漏孔快速定位的研究仍然处于初步阶段，一般利用方向规[1]定位漏孔的位置并测量其漏率。国外，Woronowicz等[2-4]通过求解无碰撞的玻耳兹曼方程获得了真空羽流的物理和数学模型，并采用直接模拟蒙特卡罗（DSMC）方法验证了模型的可靠性，还研制出一种真空羽流的自动检测实验装置：在真空腔室中设置一个可以旋转和平移的平台，将质谱仪和全压计放置在平台中心，通过平台的旋转和平移测试腔室不同位置的分压，可实现漏孔的快速定位。Fuchs等[5]发现：以液氨作为示漏工质，当氨蒸气由一定面积的小孔泄漏到超高真空环境形成羽流，可通过精确的动力学理论分析计算较好地预测羽流测量结果。新墨西哥州立大学的Cai等[6]利用DSMC方法，结合稀薄气体动力学，给出无碰撞的圆孔、环孔喷射羽流的物理及数学模型，并将此模型应用于推进器羽流的数值模拟中，为泄漏气体从高压侧向真空侧高速运动的模型建立提供了理论依据。

本文参照Woronowicz等人的仿真思路，结合Cai等人的物理模型，在分析空间站泄漏处环境因素的基础上，针对特定的环境参数设置了特定的泄漏边界条件，并以DSMC方法为工具，分析得出了典型漏孔形状和位置对泄漏处附近羽流场的影响，以期为后续实验提供数据支持。

1 仿真对象分析

空间站轨道高度为350～400 km，处于大气层的热层，大气成分主要为原子氧，且粒子数密度在1×1015/m3左右[7]；波长小于 0.175 μm 的太阳紫外辐射被热层中的大气物质所吸收，使气温随高度的增加而迅速增高，空间站外的大气温度约为1000 K[7]。因此，设置模拟温度为 1000K，泄漏处的粒子数密度为1×1020/m3[8]。由于漏孔内外压差很大，所以将气体从漏孔进入真空考虑为声速扩张，声速计算公式为

式中：k为传热系数；R为摩尔气体常数；T为漏孔孔口处的热力学温度。则上述模拟条件下的声速约为800 m/s。除此之外，还应考虑空间站不同位置处的外部结构以及漏孔的大小和形状对羽流场的影响。

真空泄漏羽流场在不考虑外部干扰因素的情况下是对称分布的，因此本文采用二维模拟。模拟设置的流场尺度为 0.5 m×0.3 m[3]，漏孔设置在流场左侧中心的位置，泄漏处管道的壁厚为1 mm[4]。相关资料显示[4]，当空间站的泄漏漏孔直径达到mm量级时就会对空间站的正常运行产生较大的影响，因此本研究将漏孔直径分别设置为1、2、3 mm。导致航天器泄漏的原因比较复杂，包括人为操作不当、部件老化或者微流星碰撞等，因此在考虑漏孔形状时不能一概而论，本研究选取张口孔、缩口孔和平行斜孔3种典型漏孔形状（如图1所示）。空间站的外部结构极其复杂，遍布管道和桁架，还有各种不同功能的腔体暴露在空间站外部，因此漏孔所处的位置可能会在任何角落，本研究选取拐角、斜边、夹角处等典型位置的漏孔（如图2所示）。仿真分析时，以上参数设置只需在软件中对几何模型进行相应修改即可。

图1 三种漏孔形状Fig.1 Three types of leak holes

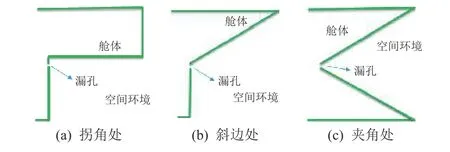
图2 漏孔处于空间站外部不同位置示意Fig.2 Locations of leak holes in the external structures of the space station

2 DSMC仿真

在描述气体粒子随机运动的过程中需要运用DSMC方法[9]，并作如下假设：

1）入口气流模型

气体通过漏孔进入流场，其中的气体粒子在孔口处均匀分布，粒子运动速度遵循麦克斯韦分布，分布函数为

粒子运动方向按照余弦定律计算。

2）气体粒子与壁面碰撞模型

气体粒子穿过漏孔时，会与漏孔的内壁发生碰撞。粒子与漏孔内壁之间相对运动的物理模型采用完全漫反射模型，粒子飞离壁面时的方向符合余弦定律，速度服从麦克斯韦分布，分布函数如式(2)所示，平均动能与壁面温度T有关。

3）气体粒子间碰撞模型

气体粒子间的碰撞模型采用可变硬球（variable hard sphere, VHS）模型[9]，对于稀薄气体来说，粒子的平均碰撞率由玻耳兹曼方程

给出。式(3)中：n为气体粒子数密度；σT为碰撞截面；cr为粒子间的相对运动速度。网格单元内粒子发生碰撞的概率pcol与σT、cr的乘积成正比[10]，

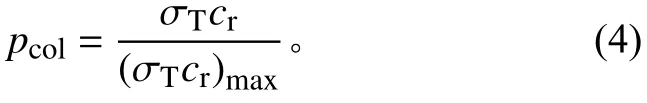
在VHS模型中，σT为cr的函数，而非恒定值，因此可以保证碰撞概率在[0, 1]之间。选择合适的时间步长，即可求出在Δt内网格单元内发生的碰撞次数

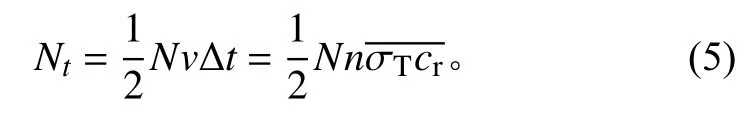
式中：N为单元内的总粒子数，其前面的系数1/2是表示2个粒子间才能发生相互碰撞[10]。

DSMC方法所采用的碰撞描述为非时间计数（NTC）法[9]，可在保持时间计数（TC）法[9]效率的同时克服TC法中的困难，并在程序开始之前事先计算出网格单元内的碰撞数。因此，可在运行碰撞程序之前预先对碰撞数进行标定，以提高运算效率。

由于空间真空环境的本底粒子密度相比于泄漏气体密度可以忽略不计，本文模拟中不考虑泄漏气体粒子与外部空间本底粒子的碰撞。粒子流物理模型的建立是为了在追踪气体分子运动时排除其他因素对追踪的影响，相对独立地计算气体分子的运动情况。在模拟大量粒子的运动时，每一个粒子的运动由一组随机变量来表达；对整个物理过程进行模拟时，进行抽样的随机数一般都在(0, 1)区间内服从均匀分布并且相互独立，每个气体粒子运动过程的模拟利用数学方法进行[6]。追踪每个模拟粒子，记录其位置和速度信息，然后对每个网格单元内的信息进行统计即可得到相应的流场压力关系。

3 空间站泄漏总体分析

3.1 漏孔孔径对羽流的影响

不同直径下的圆柱形漏孔，达到稳态后的泄漏羽流场如图3所示。可以看出，孔径对泄漏的影响较大，孔径越大漏率越大，羽流的形态会更饱满，羽流场的平均压力也就更大；且压力沿轴向单调递减，沿竖直方向对称分布，向两边递减。

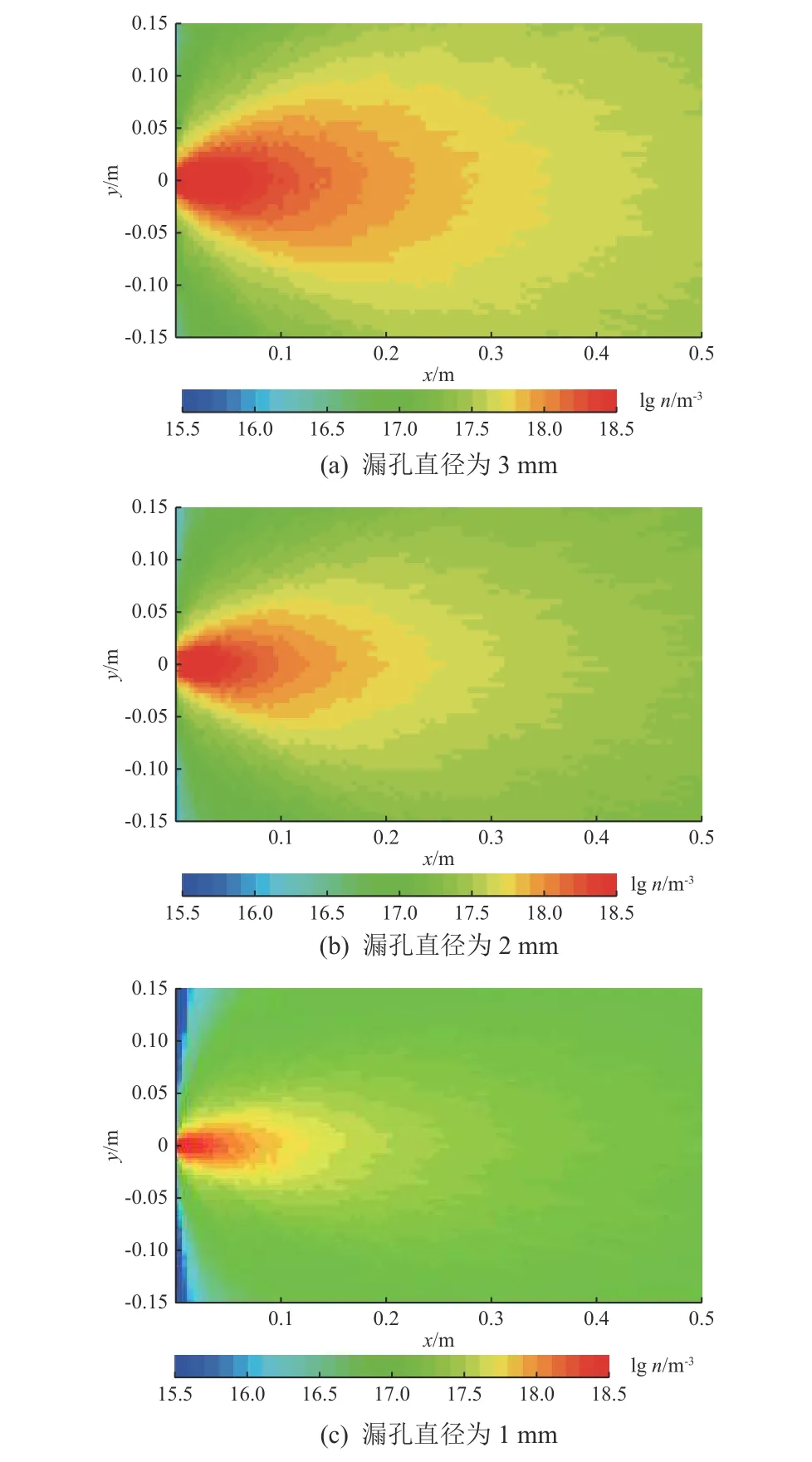
图3 不同孔径漏孔的羽流场Fig.3 The plume fields for leak holes of different diameters

3.2 漏孔形态对羽流的影响

当漏孔中间直径为1 mm时，不同漏孔形态下达到稳态后的泄漏羽流场如图4所示。可以看出，孔口形状对漏率的影响较小，但均会在一定程度上改变羽流的形态，张口孔比缩口孔的羽流场平均压力略微大一些，猜想可能是由于缩口孔的结构会对气体有阻挡作用，导致气体与壁面的碰撞次数增多，通过漏孔的粒子数减少。平行斜边的漏孔结构会显著改变气体粒子运动的方向，使得羽流场偏转一个角度，不再是对称结构。

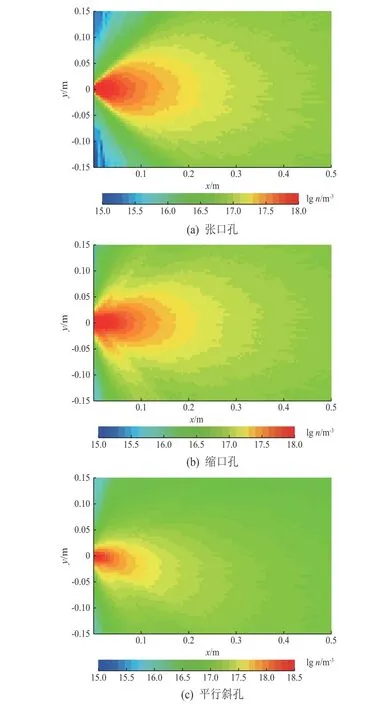
图4 不同形态漏孔的羽流场Fig.4 The plume fields for leak holes of different shapes

3.3 航天器外部形状对羽流的影响

不同位置漏孔处达到稳态后的泄漏羽流场如图5所示。可以看出，航天器的外部形状对羽流场的分布有较大的影响：拐角处的漏孔，泄漏气体粒子受到外部壁面的限制，与壁面发生碰撞后被反射，使羽流形态发生改变；斜边处的泄漏羽流会发生角度偏转；而对称夹角处的泄漏羽流场仍然保持对称形态，无明显改变。

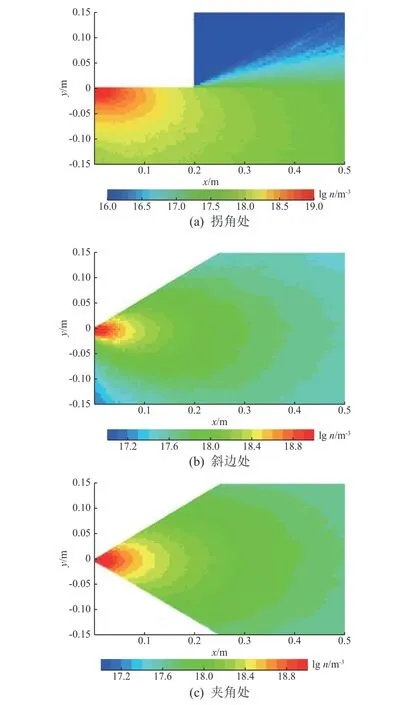
图5 不同位置漏孔的羽流场Fig.5 The plume fields for leak holes at different locations

4 结果与讨论

图6是不同孔径漏孔泄漏羽流的轴向粒子数密度随轴向距离的变化。可以看出，轴向粒子数密度单调递减，距漏孔越远密度越小。

图6 不同孔径漏孔的轴向粒子数密度分布Fig.6 Number density distribution for leak holes with different diameters in axial direction

图7是张口孔和缩口孔的轴向粒子数密度分布对比，前者比后者要大5×1016/m3左右。

图7 张口孔和缩口孔的轴向粒子数密度分布对比Fig.7 Comparison of number density distribution in axial direction between bellmouth orifice and funnel-shaped orifice

图8是中间孔径1 mm的漏孔泄漏达到稳态时，轴向距离分别为 0.1、0.2、0.3、0.4 m 处竖直方向的粒子数密度分布，可以看出粒子数密度在中间轴线处最高，向两边呈现递减的对称分布。因此，对于一般的漏孔，检漏设备在可疑位置处的竖直方向进行测量，测得的峰值位置即处于漏孔的轴线方向，该点与舱体的垂直交点即为泄漏点；对于形状不规则的漏孔，需对其竖直方向进行多次测量，获取每次测量的峰值点，这些峰值点的连线与舱体的交点即为泄漏点。

图8 竖直方向粒子数密度分布Fig.8 Number density distribution in vertical direction

由3.3节可知，空间站的外部形状会显著改变泄漏羽流场的形态。为了能够适应局部的羽流场分布，在空间站的管道交接处、舱体边缘等位置进行检漏测量时，检漏设备要以一定的角度安放，并根据测量位置所处的几何结构进行旋转和移动，以便精准定位泄漏点。

5 结束语

本文采用DSMC方法，获得了不同条件下，密封舱内气体从不同漏孔中泄漏到真空环境中的羽流场分布，并对不同情况下的检漏测量提出了建议。由于只进行了二维场模拟，与实际的三维空间粒子运动轨迹以及压力分布会有所区别。后期将开展相关的缩比实验，并将实验结果与模拟仿真结果进行比对，以期获得更加准确有效的泄漏测量及定位方法。为保证羽流的形成，选择的实验腔体要模拟在轨条件，因此要尽可能的大，以减少气体与器壁的碰撞；另，抽气系统需要提供均匀抽气，如令整个腔体的壁面都为低温冷面吸附气体，以降低抽气对气体粒子运动的定向作用。