统计能量分析方法用于卫星天线结构声振响应预示的有效性研究

陈 曦，刘 刚，谢伟华，林勇文，刘 波

（中国空间技术研究院 通信卫星事业部，北京 100094）

0 引言

航天器在发射主动段的动力学环境十分严酷，其中包括高量级的振动环境和高声压级的噪声环境，噪声频率从低频10 Hz到高频10 000 Hz。整流罩内的噪声环境会使航天器，尤其是具有较高结构系数（结构面积与其质量之比）的结构产生较大的加速度响应[1]。

卫星天线是典型的高结构系数部件，是卫星结构中对噪声环境最为敏感的部件之一。在卫星天线的研制过程中，需要采用噪声试验来考核天线结构强度，进而验证结构设计方案的正确性；而在试验前开展噪声环境预示，可以指导单机试验、结构设计等工作，尽早发现问题，减少损失。

NASA于2001年发布的 NASA-HDBK-7005《动力学环境准则》[2]，在噪声分析中引入边界元法，将有限元方法（FEM）拓展到高频，将统计能量分析（SEA）方法拓展到瞬态动力学范围，提高了SEA耦合损耗因子的估计精度，在声学空穴分析中发展了填充系数法等。由此可知，噪声预示需要结合运用有限元、边界元以及统计能量法等进行全频段分析。目前，国外先进卫星制造商在天线设计过程中，大都在进行天线噪声试验前先进行噪声分析，而且分析结果与试验结果吻合较好[3]。

我国对噪声环境预示分析也开展了很多研究工作。文献[4-5]介绍了航天器噪声环境预示方法，包括有限元分析法、边界元方法、统计能量法等，同时推荐了噪声分析软件，包括VA One、Auto SEA等。文献[6]利用SEA方法进行了卫星太阳翼的声振力学环境预示，介绍了SEA方法的分析步骤和参数选取，验证了该方法的可行性。文献[7-8]利用SEA方法进行声振分析，并对参数选取进行了研究。

本文以卫星天线为例，在有限元分析中引入统计能量方法，建立天线的SEA模型，研究统计能量参数对计算结果的影响，通过与试验结果进行对比，确定统计能量参数的取值范围，并验证该声振响应方法用于天线结构噪声振动响应预示的有效性。

1 统计能量分析方法理论

统计能量分析方法的理论基础是室内声学和统计力学，主要应用于较高频段的振动分析。为了建立能量平衡方程，将结构按照其模态特性划分为多个子系统，并建立各子系统之间的能量输入、传递以及损耗的关系，求解各子系统的能量，最终得到系统的响应[9]。

N个子系统有N个能量平衡方程，它们的矩阵形式为

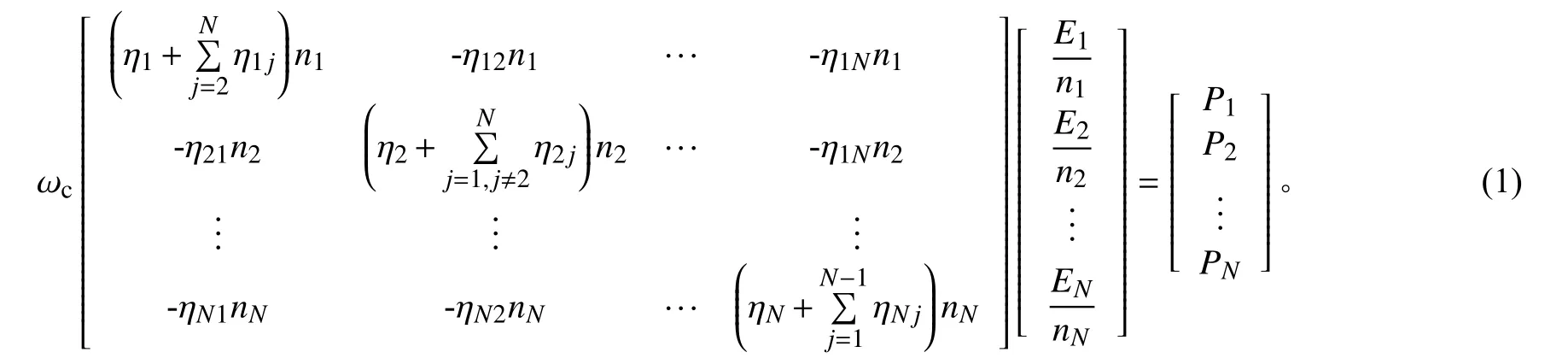
式中： ωc为 中心频率；Ei(i=1,2,···,N)为子系统i的能量；ni(i=1,2,···,N)为子系统i的模态密度；Pi(i=1,2,···,N)为子系统i的输入功率；ηi(i=1,2,···,N)为子系统i的内损耗因子；ηij(i=1,2,···,N;j=1,2,···,N)为子系统i与子系统j的耦合损耗因子。

由式(1)可以看到，复杂系统在应用统计能量方法时需要确认的参数包括模态密度、输入功率、内损耗因子以及耦合损耗因子。参数确定后即可求解方程(1)，得到各子系统的能量，再将能量换算成相应的加速度就完成了响应预示工作。式(2)中：f为天线子系统的固有频率；M为天线子系统的有效质量。

文献[10]利用统计能量法，将某小卫星划分为26个子系统和97个连接，然后对整星的宽带声振力学环境响应进行了预示。该文献给出的复杂结构的SEA步骤如下：

1）按照共振模态将结构划分为不同的子系统单元；

2）确定各子系统之间的连接方式；

3）确定子系统的模态密度、输入功率、内损耗因子和耦合损耗因子；

4）求解子系统能量；

5）计算出子系统的动力学响应。

2 卫星天线声振响应分析建模

图1为卫星天线在混响室进行噪声试验的状态，图2以1～9的编号标注了天线上的测点位置。

图1 天线噪声试验现场Fig.1 Antenna under acoustic test

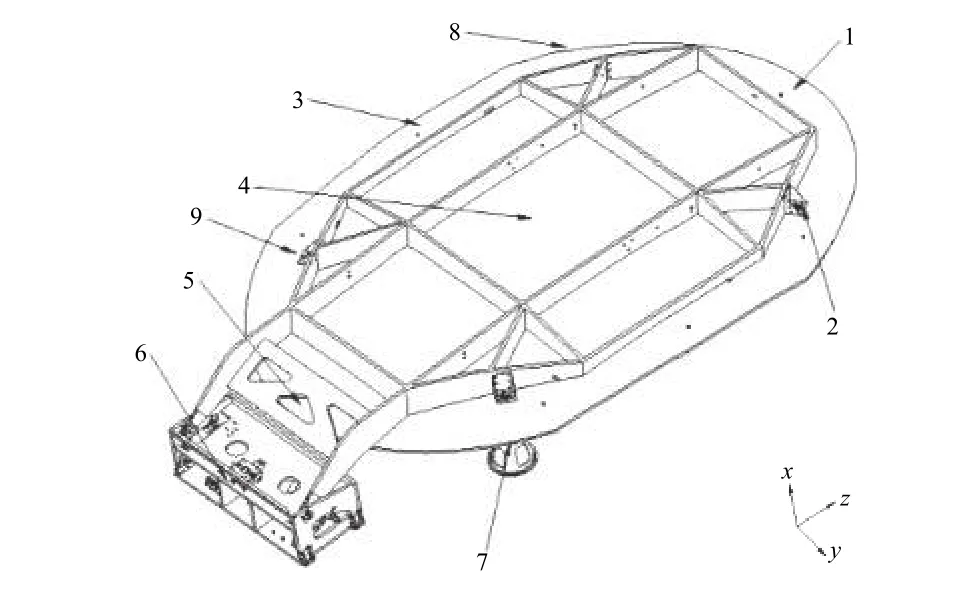
图2 天线测点分布Fig.2 Measurement points of the antenna for acoustic test

目前，天线的动力学响应分析计算局限于有限元方法，但由天线反射面模态密度（图3）可见，天线在中高频区域的结构模态比较密集；为了更加准确地描述结构高频模态振型，在建立FE模型时需要将网格划分得非常密集，带来巨大的计算量。为降低计算压力，建立SEA模型进行天线的声振分析。

采用统计手段分析出子系统的平均响应，建立子系统的SEA模型，获得子系统的SEA参数——模态密度、内损耗因子和耦合损耗因子等，建立功率流平衡方程；然后通过求解方程得到子系统的平均能量，进而计算得到子系统的位移、速度和加速度响应。

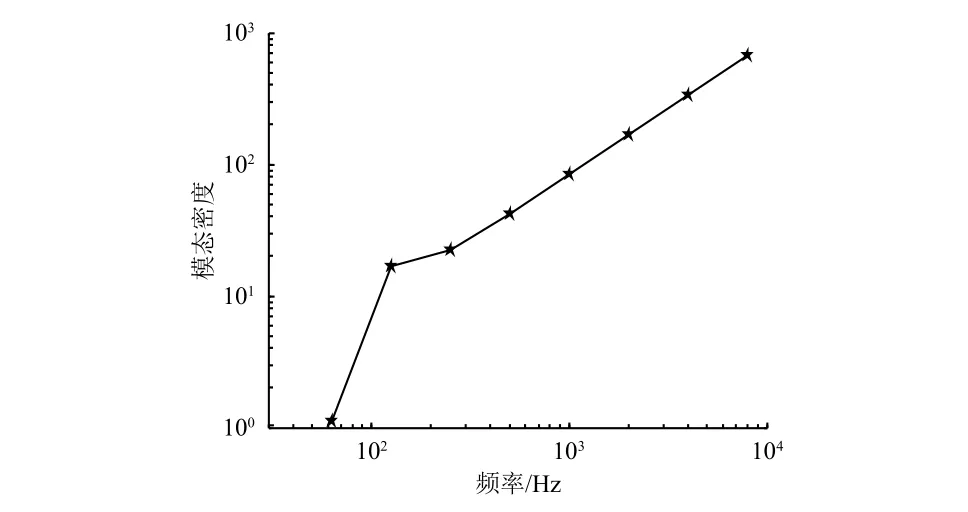
图3 天线反射面模态密度Fig.3 Modal density of the antenna

统计能量分析方法建模中，子系统划分是基于子系统在关注的频带内所有共振的模态之间能量等分的假设，其中子系统的特性是根据统计手段获得的，故而精度不高，但已经符合工程要求，可以用于天线反射面的SEA建模。

SEA建模时，将卫星天线反射面划分为1个子系统，混响声场划分为2个半无穷声场（semiinfinite field, SIF）子系统，用VA One软件[11]建立卫星天线反射面的声振响应分析模型，如图4所示。

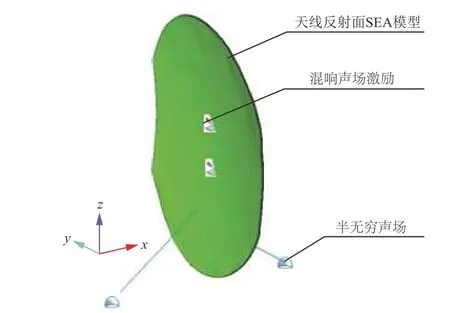
图4 天线反射面SEA模型Fig.4 SEA model of the antenna

2.1 声场模型

建立整星声场统计能量模型，用半无穷声场和混响声场（diffuse acoustic field, DAF）模拟混响场，模型声压与天线噪声试验条件（表1）保持一致。

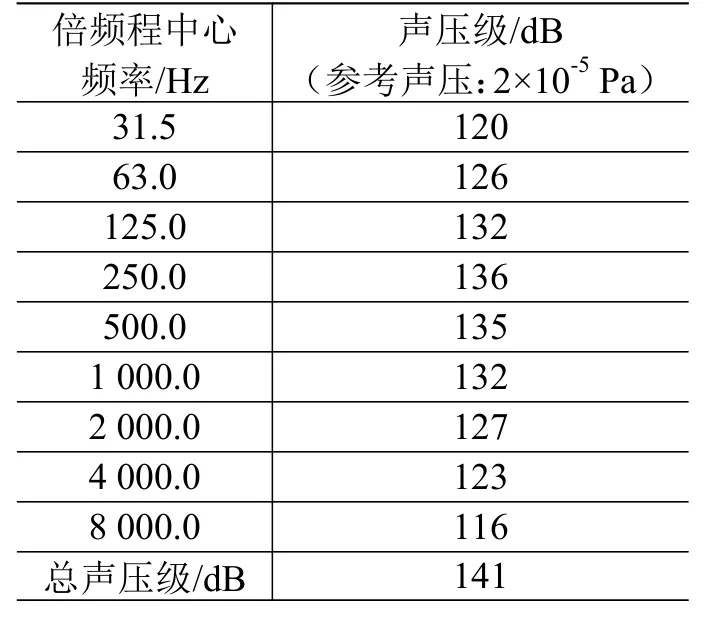
表1 卫星天线噪声试验条件Table 1 Acoustic test level of antenna

混响声场产生的随机压力谱以面载荷的形式作用在天线表面，建立声场模型后，计算可得到结构的输入功率，如图5所示。

图5 声场对卫星天线结构的输入功率Fig.5 Power input of the acoustic field for the satellite antenna structure

2.2 结构统计能量分析模型

天线反射面是由复合材料面板和铝蜂窝芯子组成的夹层板结构，在VA One软件中建立此类结构板的SEA模型。其中，结构板的模态密度可计算得到；本文将天线反射面划分为1个子系统，故不存在耦合损耗因子。

在SEA中，内损耗因子是结构的临界模态阻尼比的2倍[12]，因此结构的随机响应受内损耗因子影响比较大。目前，在工程研制中，卫星天线的结构内损耗因子主要依据经验或者试验结果来确定，其数值一般在1%左右；也可以根据其他类似结构的噪声试验结果来反推。在考虑声场对结构的影响时，子系统的内损耗因子还需要加上结构声辐射损耗因子，因此总的损耗要比结构的阻尼大很多。在VA One软件中，声辐射的损耗因子由软件自行分析计算得出，而结构的内损耗因子作为影响统计能量计算的参数需要合理给出。

下文选取一组不同的结构内损耗因子，计算天线反射面的平均加速度响应，通过与试验结果对比获得合适的内损耗因子参数值。

3 卫星天线声振响应分析预示

建立统计能量分析模型，选取不同的结构内损耗因子，分别计算天线反射面的声振响应，得到不同的响应加速度。并将声振分析结果与天线噪声试验响应结果的平均值进行对比，方均根加速度对比见表2，功率谱密度对比见图6。由表2可以看出，内损耗因子选为0.5%时，卫星天线的方均根加速度响应分析结果与试验结果间的相对误差最小。

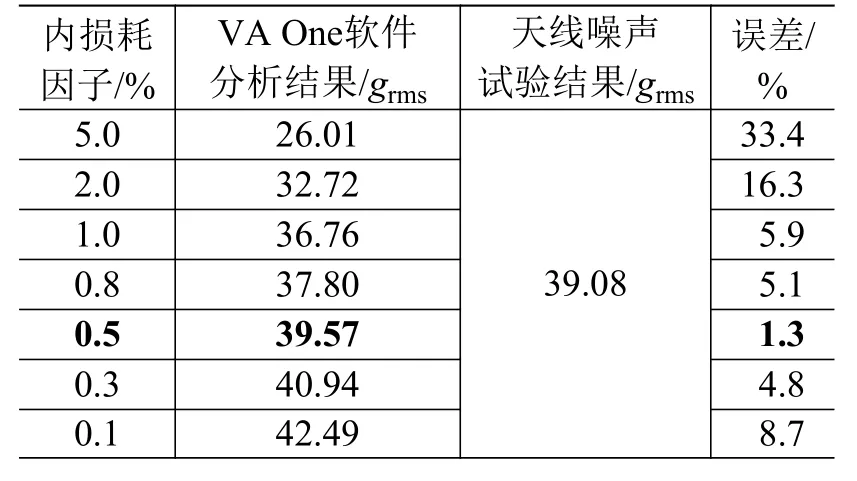
表2 不同内损耗因子下声振预示与试验结果对比Table 2 Comparison of analytical and test results for vibroacoustic response (in grms) with different damping loss factors

图6 不同内损耗因子下声振分析与试验结果对比Fig.6 Comparison between analytical and test results for vibro-acoustic response (in PSD) of an antenna with different damping loss factors

由图6可以看出，功率普密度分析结果与试验结果在内损耗因子取值≤5.0%时相差不大，内损耗因子≤1.0%的3条曲线间差别细微。

综合表2和图6分析结果与试验结果的对比可知，对类似第2章所分析结构的反射面天线，取内损耗因子为0.5%结果较优。

4 结束语

本文开展了卫星天线的统计能量分析建模及声振响应分析，并将计算结果与试验结果进行对比，表明统计能量分析方法可以有效应用于卫星天线声振响应预示，但需要选取合适的结构内损耗因子。本文所分析的反射面天线在内损耗因子取0.5%时结果较优。这一结论亦可应用于类似结构的声振分析预示。