一种柔性多体动力学建模方法及其工程应用

葛东明，史纪鑫，邓润然，范晶岩

（北京空间飞行器总体设计部，北京 100094）

0 引言

随着航天技术的发展，航天器由带单轴驱动太阳电池阵形式向着大挠性多体方向发展，例如空间机械臂、双轴驱动太阳电池阵、多自由度驱动天线等。这种刚体和柔性体的混合系统，在各体之间存在大范围转动运动的同时，还叠加着弹性振动。复杂的刚柔耦合动力学效应，以及与控制系统的控制-结构交叉耦合，使得在这类复杂航天器的动力学特性分析，特别是GNC控制方案验证中，对柔性多体动力学模型的需求十分迫切[1-4]。

随着航天器功能的复杂化，航天器逐渐呈现出构型时变、多级驱动、柔性化等特征[5-14]。具体表现在：1）动力学问题越来越突出，系统构型实时变化，准静态建模方法已经无法适应，系统模型必须对构型的变化具有连续性；2）复杂的动力学特性与控制系统耦合越来越紧密，总体指标分配和系统性能验证越来越依赖于仿真，且对动力学建模的精细化程度要求越来越高；3）模型越来越复杂，由简单的准静态、线性模型向柔性、多体、非线性模型发展，对变构型重构模型、柔性多体模型的需求越来越多。

本文针对具有多轴天线驱动、机械臂运动、空间站舱段转位等多体运动特征的航天器，基于拉格朗日方程和有限元方法，给出一种柔性多体动力学建模方法。此方法适用于开链式拓扑结构，所建立的动力学方程考虑了大角度刚体相对转动、弹性部件振动和柔性关节变形特性。将该柔性多体动力学建模方法程序化并应用于工程实际，可实现完全自主的动力学建模、模型代码输出和控制联合仿真功能，为此类航天器的动力学特性分析及其控制系统设计与系统级仿真验证服务。结合工程实际对象，与商业柔性多体软件Adams进行对比，验证了该建模方法及其软件实现的正确性和通用性。

1 动力学模型

采用第二类拉格朗日方程，针对浮动基座、树形开链式拓扑结构、线性小变形的柔性多体类航天器，建立其柔性多体动力学模型。航天器力学模型为树形拓扑结构，由本体、部件和关节组成，如图1所示。其中，Oixiyizi是惯性参考系，Obxbybzb是本体参考系，Oaixaiyaizai是部件i参考系，Otixtiytizti是关节i参考系。本体可以自由运动；部件和本体之间，以及相邻部件之间通过关节连接。本体是以惯性空间为参考的刚性体；部件可以是刚性结构，也可以是柔性体结构，部件之间由驱动关节连接，弹性体和关节顺序命名。

图1 树形拓扑结构的力学模型Fig.1 Mechanical model in tree topology

1.1 柔性体建模

针对图1中的第i个部件建立其动力学模型，其无阻尼自由振动方程可写为

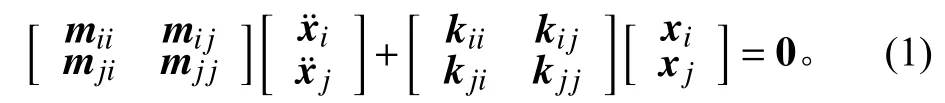
式中：mii、mij、mji、mjj为质量矩阵；kii、kij、kji、kjj为刚度矩阵；xi为内部节点响应；xj为界面节点响应。

采用Craig-Bampon模态法[15]可得部件i的物理自由度与模态坐标的关系为

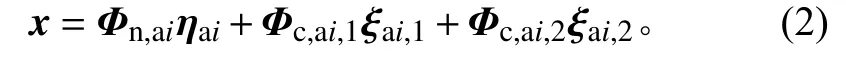
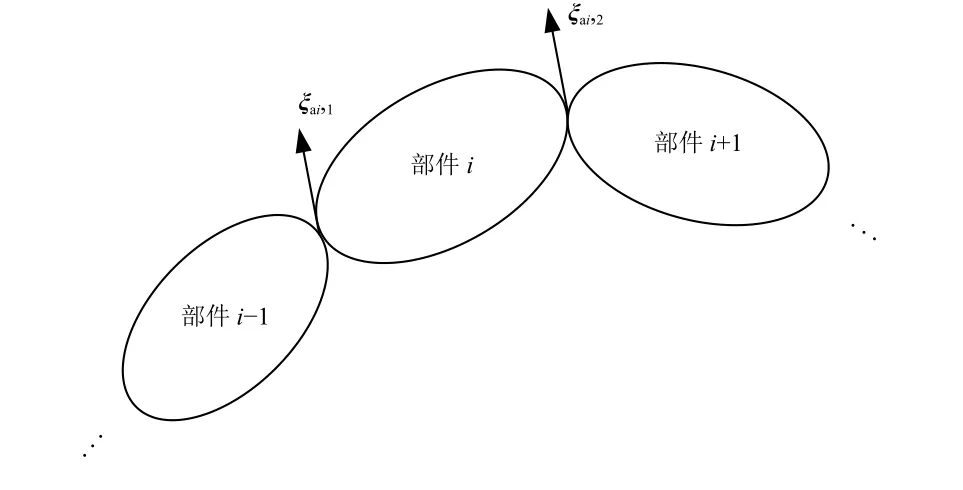
图2 柔性体连接示意Fig.2 Flexible body connections

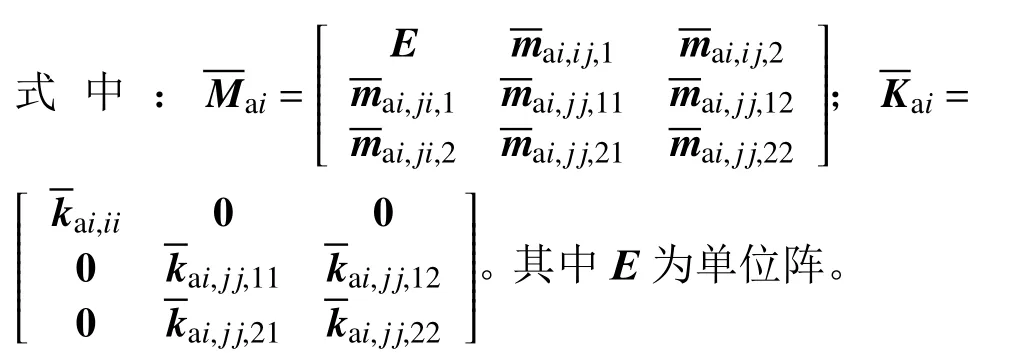
由于本文推导采用相对坐标形式，需将界面点ξai,1和 ξai,2由绝对坐标变换为相对坐标。将界面点ξai,2重新定义为在部件参考系Oaixaiyaizai下的相对坐标

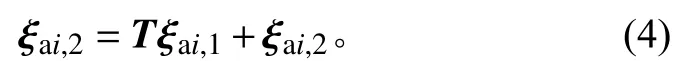
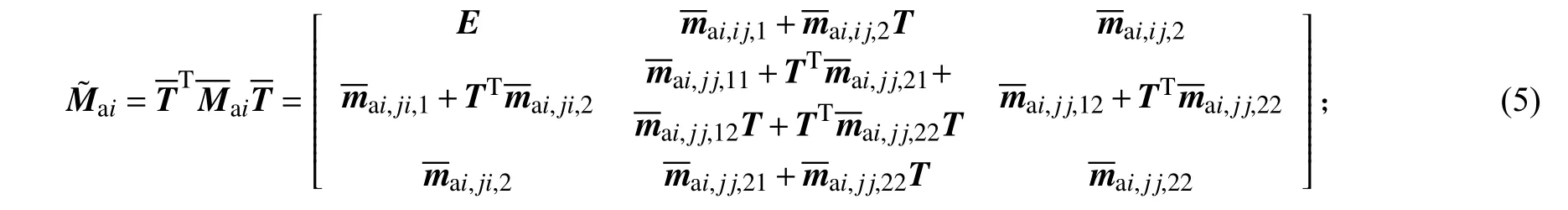
基于方程(5)、(6)，部件i的动能和势能描述分别为：

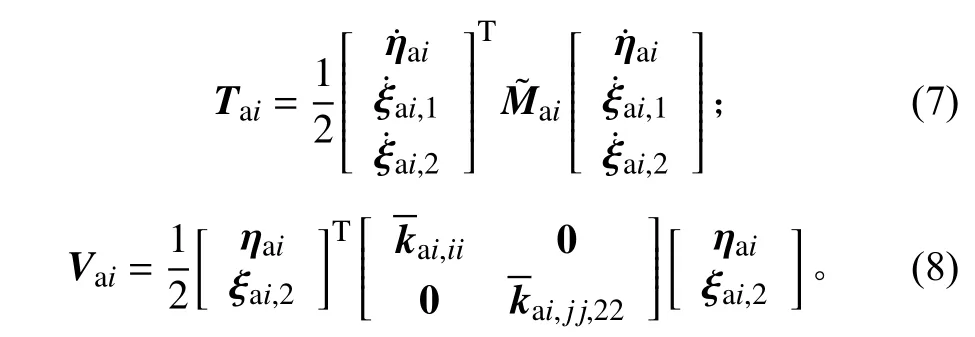
当部件i考虑为刚体时，其势能为0，且动能描述可简化为

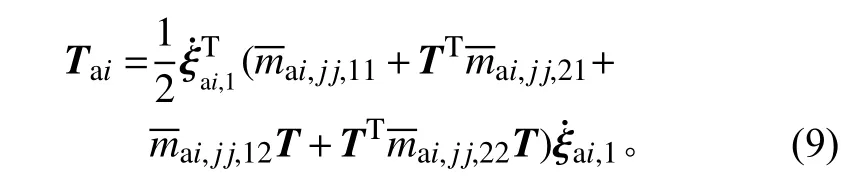
1.2 柔性关节建模

柔性关节模化为质量-弹簧系统（如图1所示）：质量反映电机的惯性；弹簧反映电机的驱动刚度，由3个线弹簧和3个卷簧组成。关节的动能和势能描述分别为：

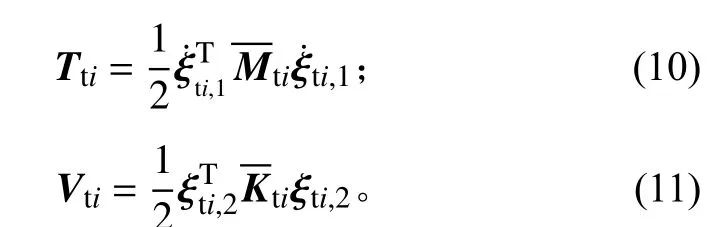
1.3 系统动能和势能

根据各部件和关节之间的界面连接关系，系统动能和势能可以由如下条件获得。

1）当关节i连接部件i-1时，连接关系为

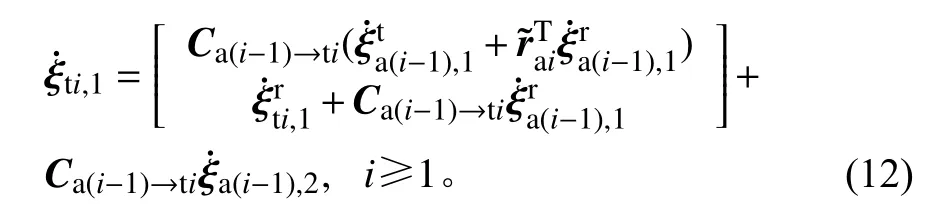
当i=1时，下标0代表本体。

2）当部件i连接关节i时，连接关系为

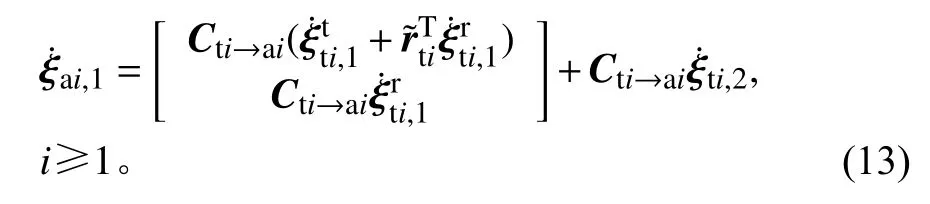
其中：Ca(i-1)→ti为部件i-1参考系Oa(i-1)xa(i-1)ya(i-1)za(i-1)到关节i参考系Otixtiytizti的变换矩阵；Cti→ai为关节i参考系Otixtiytizti到部件i参考系Oaixaiyaizai的变换矩阵；rti为界面点 ξti,2在关节i参考系Otixtiytizti下的位置矢量。上标t和r则分别代表相应物理量的平动分量和转动分量。

利用连接关系式(12)和(13)，系统动能和势能的一般描述分别为：

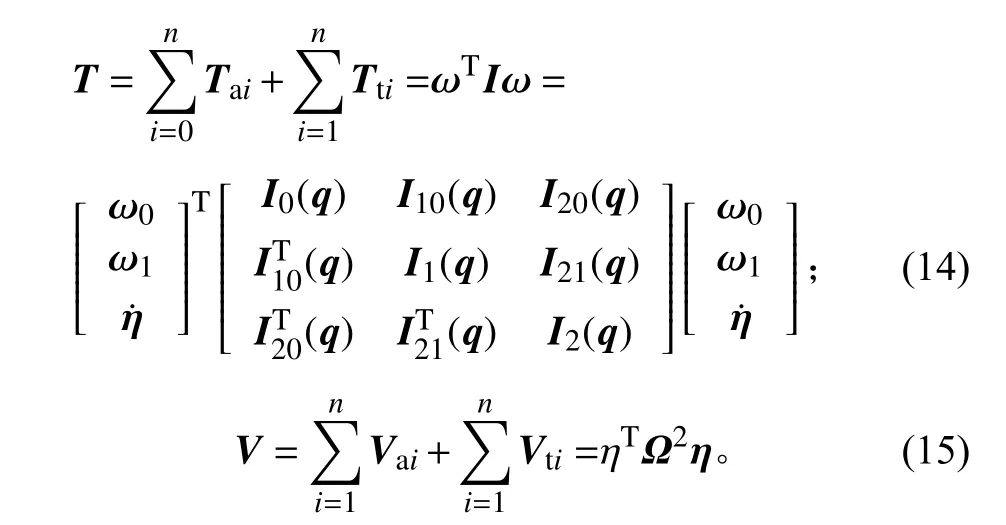
式(14)、(15)中：ω0=[vbωb]T，vb和ωb分别为本体平动速度和转动角速度；为沿着驱动轴的关节角速度；为广义质量矩阵，是关节角q的函数，q=[q1q2……qn]T，qi为沿着驱动轴的关节角；Ω为广义刚度阵。

1.4 系统动力学方程

根据第二类拉格朗日方程，利用方程(14)和(15)的偏导数，获得刚柔耦合动力学方程

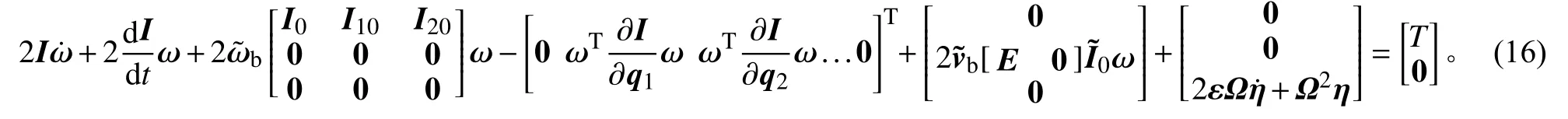
由上述动力学建模过程可知，本建模方法具备以下特点：1）对于浮动基座、树形开链式拓扑构型、线性小变形结构都是适用的；2）基于结构有限元模型建立柔性动力学方程，对一般线性结构是通用的；3）基于矢量力学的矩阵矢量运算，便于软件实现；4）通过模型代码生成或封装，便于与控制系统的联合仿真和验证。

2 工程应用实例

2.1 带多轴驱动天线的整星动力学建模

某卫星天线带有多轴驱动机构，为了评估天线驱动过程对本体姿态的影响，需要将整星柔性多体动力学模型与姿态控制系统联合仿真，传统的柔性耦合动力学分析已经无法适应，须建立整星多级柔性链动力学模型。

模型由卫星本体、两侧单轴驱动太阳电池阵、三轴驱动天线结构、三轴驱动柔性关节组成。采用第1章给出的柔性多体动力学建模方法，能够模拟电机驱动下天线的运动过程，并获得结构在运动过程中的实时动力学特征（结构的频率和振型），直接供控制分系统进行仿真分析。建模中，将两侧太阳电池阵和天线反射面作为柔性体考虑，卫星本体、驱动臂和天线基座作为刚性体考虑，同时考虑电机关节驱动刚度。

下面给出本文的柔性多体动力学建模方法与商用软件Adams仿真结果的对比分析。

1）系统频率对比：将太阳电池阵锁定，天线关节锁定，求解系统频率，本文方程与Adams软件的对比结果如表1所示，可以看出二者的一致性较好。

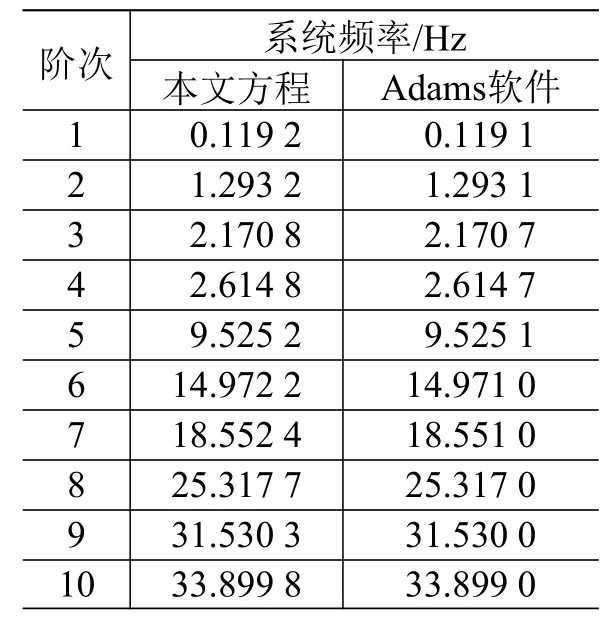
表1 本文方程与Adams软件模型的系统频率对比Table 1 Comparison of system frequency between the flexible multi-body dynamic equation and Adams model

2）时间响应对比：将太阳电池阵锁定，对本体施加6个方向的力和力矩，以及天线3个关节的驱动力矩，即方程(16)中的输入为T=[-20 N 10 N 30 N-5 N·m 10 N·m 30 N·m 0.5 N·m 0.5 N·m 0.5 N·m]。本文方程和Adams软件求得的系统时间响应对比如图3所示，可以看出二者的一致性较好。

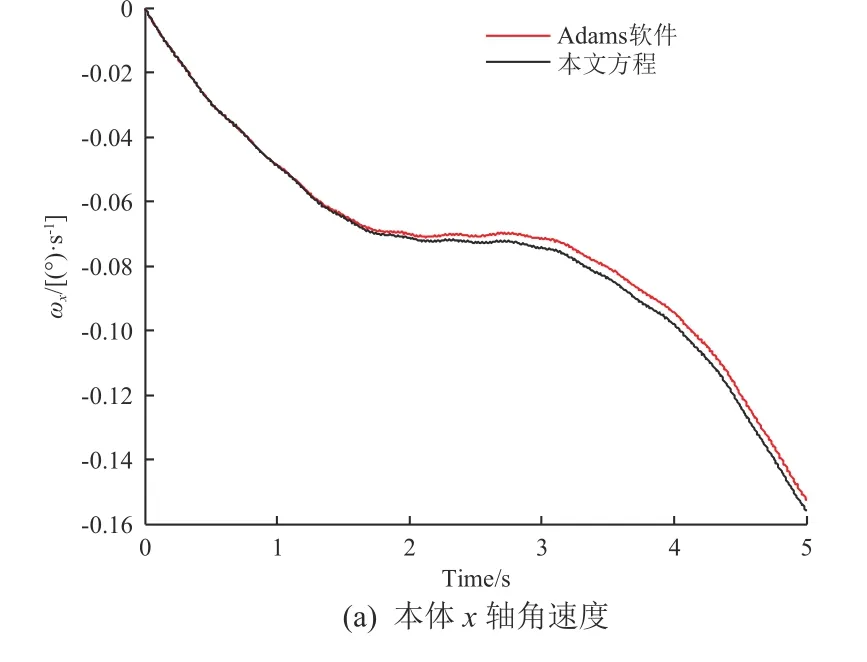
图3 本文方程与Adams软件模型的时间响应对比Fig.3 Comparison of time response between the flexible multi-body dynamic equation and Adams model

2.2 带大型柔性天线的整星动力学建模

未来航天器上应用的大型可展开天线的口径可能会越来越大，性能指标也会更加严格，而卫星姿轨控、热致振动等导致的机械运动必然会引起大型反射面天线的振动，影响天线电性能乃至任务完成质量。某整星对象是由大口径网状天线、多关节大型伸展臂、太阳电池阵与卫星本体组成的大惯量低频刚柔耦合系统，呈现出典型的大挠性体特征。

天线的点波束指向精度和稳定度对网状天线扰动非常敏感。天线在轨振动影响分析和振动抑制效率分析的基础是整星刚柔耦合动力学模型，其是整星动力学、姿态控制、振动抑制多回路系统级建模的重要组成部分。建模中，将两侧太阳电池阵和大型网状天线作为柔性体考虑，卫星本体作为刚性体考虑。

下面给出本文的柔性多体动力学建模方法与商用软件Adams仿真结果的对比分析。

1）系统频率对比：将太阳电池阵锁定，求解系统频率，本文方程与Adams软件的对比结果如表2所示，可以看出二者的一致性较好。

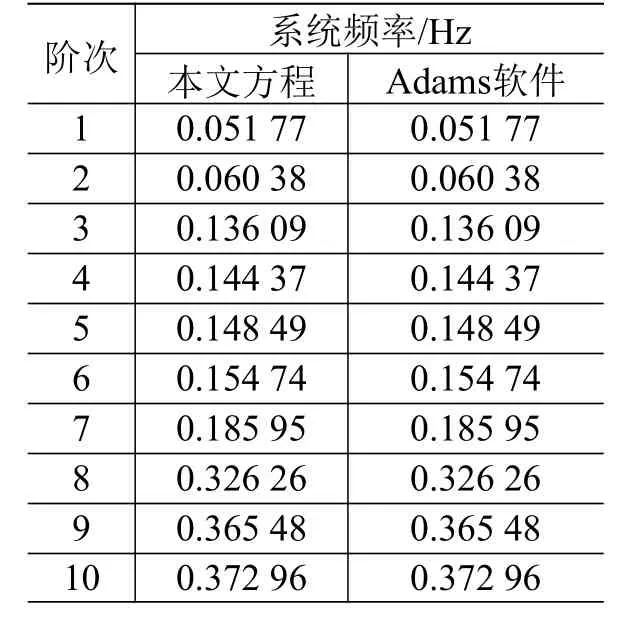
表2 本文方程与Adams软件模型的系统频率对比Table 2 Comparison of system frequency between the flexible multi-body dynamic equation and Adams model

2）频率响应对比：将太阳电池阵锁定，以质心系y轴力矩为输入，以天线反射面远端节点为输出，计算系统频率响应。本文方程与Adams软件的对比结果如图4所示，可以看出二者一致性较好，其中高频区的差别源于二者模态阶数选择的差异。

3）时间响应对比：对本体施加6个方向的力和力矩，以及太阳电池阵2个方向的驱动力矩，即方程(16)中的输入为T=[10 N 2 N -5 N·m -2 N·m 7 N·m -8 N·m 1 N·m -2 N·m]。本文方程和Adams软件的系统时间响应对比结果如图5所示，可以看出二者的一致性较好。

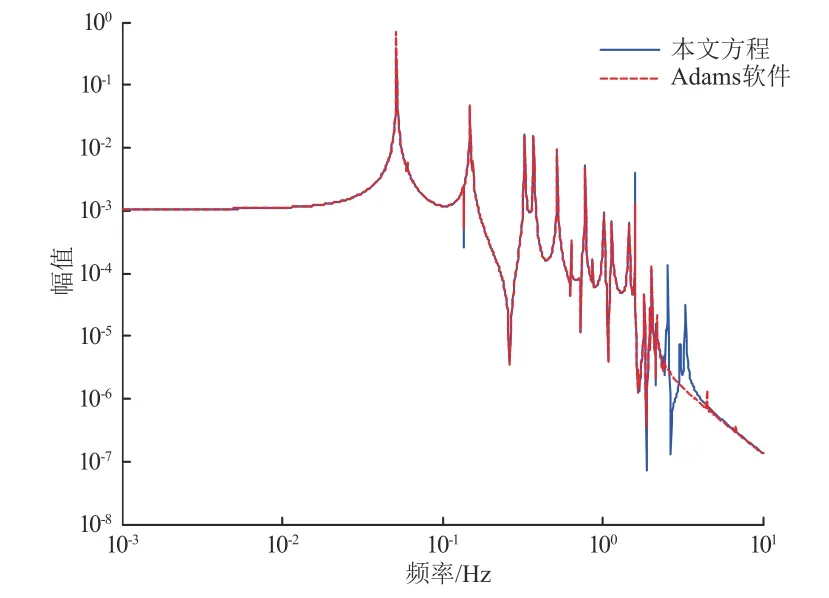
图4 本文方程与Adams软件模型的频率响应对比Fig.4 Comparison of frequency response between the flexible multi-body dynamic equation and Adams model

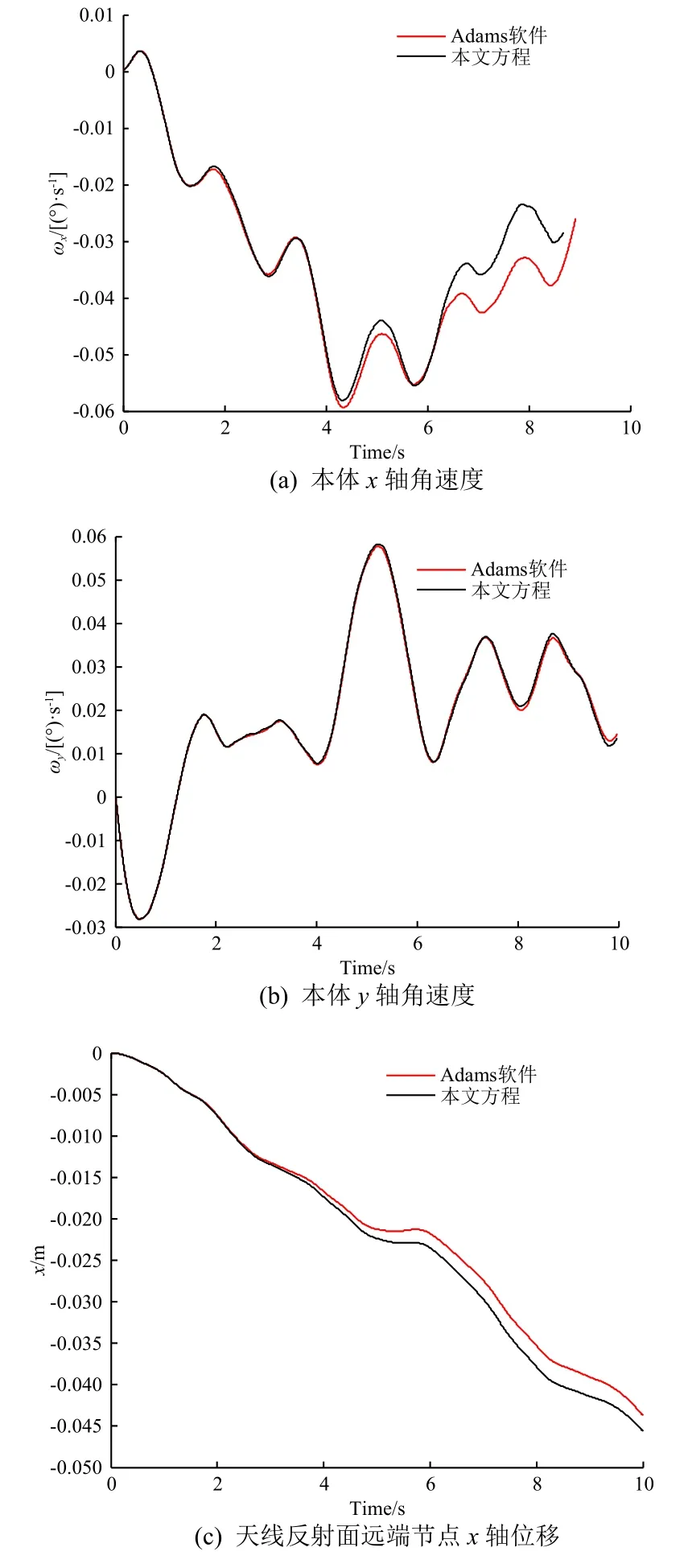
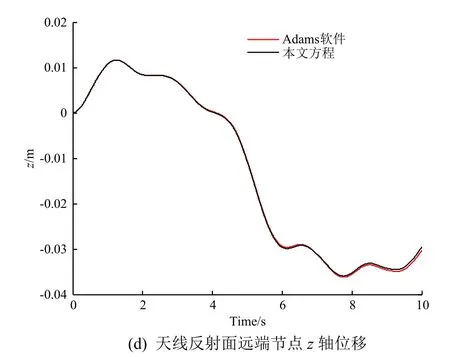
图5 本文方程与Adams软件模型的时间响应对比Fig.5 Comparison of time response between the flexible multi-body dynamic equation and Adams model

3 结束语

本文给出了一种柔性多体动力学建模方法，将其程序化并应用到带多轴驱动天线及大型柔性网状天线的整星动力学建模中。此方法适用于开链式拓扑结构，所建立的动力学方程考虑了大角度刚体相对转动、弹性部件振动、柔性关节变形特性，结构体为有限元模型，具有工程实用性。与商用软件Adams仿真结果的对比验证了本文方法的有效性。

该柔性多体动力学建模方法所建立的动力学方程形式紧凑、计算量小，将其程序化并应用于工程实际，可解决航天器复杂的机构运动与弹性振动的耦合动力学建模问题，实现完全自主的动力学建模、模型代码输出和与控制系统联合仿真功能，为此类航天器的动力学特性分析及其控制系统设计与系统级仿真验证服务。