大型复杂航天器组装动力学建模方法与应用

史纪鑫，葛东明，范晶岩，邓润然

（北京空间飞行器总体设计部，北京 100094）

0 引言

固定界面模态综合法由Craig和Bampton于20世纪60年代提出[1-2]，后续又发展出自由界面模态综合法和混合界面模态综合法。模态综合法把整个结构系统视为由若干子结构组成，首先对规模小得多的子结构逐个进行模态分析或试验，然后借助子结构交界面上的连接条件，将各子结构的模态参数综合装配起来，以获得整个系统的主要模态特性。

大型空间复杂结构系统，特别是增长式结构和变结构系统的广泛应用，对直接采用有限元计算进行结构动力学分析提出了严峻的挑战[3-4]。模态综合“化整为零，积零为整”的分析思想具有现实的应用基础[5-7]，特别适合于部件分散加工、制造、集成的特点，在计算效率、子结构级地面试验和修正方面具有先天的优势，可以服务于大型复杂空间结构系统的结构动力学分析，以及向柔性多体动力学的延伸应用[8-12]。但截至目前国内尚未见有关模态综合技术在大规模复杂空间结构分析中的适用性研究的文献报道。

本文基于固定界面模态综合方法给出复杂航天器结构组装模型并完成技术的软件实现，研究其对复杂空间结构动力学分析的有效性。

1 理论模型

1.1 子结构动力学方程

一个完整结构被分割为若干子结构体后，其子结构体无阻尼的振动方程可写为

式中：m为质量矩阵；k为刚度矩阵；f包含有耦合结构连接处的内力；x是节点响应。

在实际应用中，结构体的有限元模型规模往往很大，必须采取模态坐标刻画结构的弹性振动。根据内部坐标和界面坐标，将式(1)划分为

式中：xi为内部节点响应；xj为界面节点响应；fj为耦合界面连接内力。

对于固定界面有xj=0，由式(2)可获得子结构自由振动方程

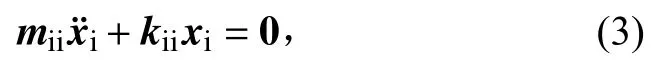
于是，可求得系统第n阶正则模态，满足：

其中：ωn为固定界面第n阶频率。假设φii=[φ1,φ2,···,φn]，则子结构的正则模态集为

其中Φn是将高阶模态截断的低阶正则模态集。

对式(2)，其静力方程为

由式(7)可以得到

式中：I是单位矩阵。当只有一个界面节点时，Φc即为刚体模态。因此，子结构模态矩阵由其正则模态集和约束模态集构成，即

此模态集具有如下3个特性，其可以作为编程计算的正确性校验工具。

1）特性1

式中：rank(*)为矩阵的秩；numrow(*)为矩阵的行数。

式中：ηi为正则模态集的模态坐标；ηj为约束模态集的模态坐标。显然，由式(14)可以得到ηj=xj，即约束模态坐标就是界面物理坐标。

利用坐标变换(14)，将动力学方程(1)变换到模态空间，并考虑模态阻尼项，可得

式中，ξn为正则模态阻尼比。当只有一个界面节点时，即为结构相对于此节点处参考系的质量特性矩阵，且=0。

1.2 系统动力学方程

建立带阻尼项模态综合的系统振动方程时，考虑两个子结构的连接问题。根据式(15)给出两个子结构A和B在模态坐标下的运动方程

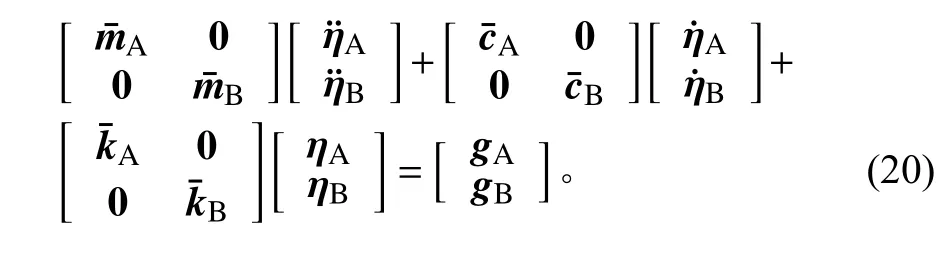
对于刚性连接，有界面协调方程

其中CBA为结构B到结构A的界面节点坐标变换矩阵。由约束模态坐标等于约束物理坐标，得ηjB=CBAηjA。选择系统广义坐标为

其中Γ为系统自由度变换矩阵。利用式(23)，可将式(20)变为用独立坐标q描述的系统振动方程

其中：

由于式(24)中没有考虑耦合系统的输入输出关系，所以只能满足耦合系统的频率计算。为实现耦合系统的时间响应和频率响应的计算，在式(24)基础上，加入由结构A（输入）到结构B（输出）的传递通道

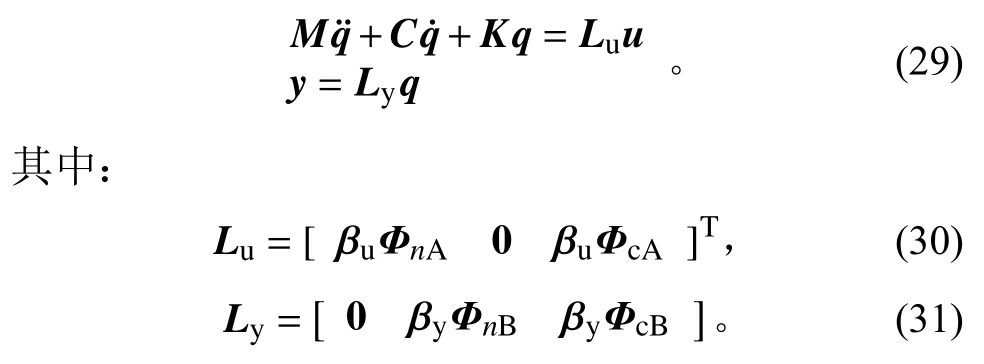
式(29)～(31)中：u为作用在结构A上某节点的力和力矩激励输入；y为结构B上某节点的位移响应输出；βu、βy是对输入节点和输出节点的模态矩阵的选择矩阵。将式(29)改写为状态空间形式

从式(32)可以进行时域仿真，得到输入激励作用下的节点位移响应。为了得到频域响应，对式(32)进行拉氏变换即可，得到从输入到输出的传递特性如下：

2 软件实现

2.1 拓扑结构及自由度描述

软件实现的难点在于系统自由度变换矩阵Γ的自动求取，为此需要先描述系统的拓扑结构和自由度。借鉴多体动力学拓扑描述方法，引入符号标签描述拓扑结构和自由度。S为子结构标签，N为界面点标签，K为关键点标签，M为正则模态标签，C为坐标转换阵标签。‘S1M50'表示子结构1的50阶正则模态自由度，‘S2N1'表示子结构2上界面点1的六个自由度。系统的拓扑结构如图1所示。

图1 拓扑结构示意Fig.1 Schematic diagram of the topology structure

2.2 软件架构设计

软件架构分为预处理模块、系统装配模块、输入输出配置模块、载荷设置模块、模态分析模块、时域分析模块、频域分析模块。

预处理模块主要完成子结构界面点设置、模型缩聚、轮廓提取，并对子结构进行降阶处理，最终获得子结构的广义质量阵、广义阻尼阵和广义刚度阵，其表达式见式(16)～(18)。

系统装配模块主要完成连接界面点匹配与坐标转换阵定义，根据装配关系自动生成系统自由度变换矩阵Γ。软件能够可视化输出装配后系统结构，如图2所示。

图2 装配后系统结构图Fig.2 System structure diagram after assembly

输入输出配置模块主要完成系统输入输出配置，自动生成配置矩阵，形成系统状态空间方程。

载荷设置模块主要实现载荷定义和添加，支持载荷曲线浏览和通道、方向的配置。

模态分析模块主要计算系统各子结构质量特性、频率特性和耦合系数，同时计算系统综合后的模态频率、模态振型、质量特性等。

时域分析模块主要计算关键节点上的位移、速度和加速度响应，同时可输出部件界面上的载荷响应。

频域分析模块可根据指定的输入和输出，计算系统的传递函数。

3 应用算例

以空间站三舱组合体为算例，验证模态综合算法的有效性。总节点数约115万，单元数约116.5万。模型如图3所示，将整舱按照舱段拆分为三舱子结构，计算3个子结构的缩聚模型，对各子结构分别取50阶模态，再对3个子结构缩聚模型进行模态综合。将该模态综合频率与原始整舱有限元模型的无阻尼自由振动的自由频率进行对比，结果如表1所示。可见，频率相对偏差在前7～15阶范围内小于1%，具有极高的计算精度。

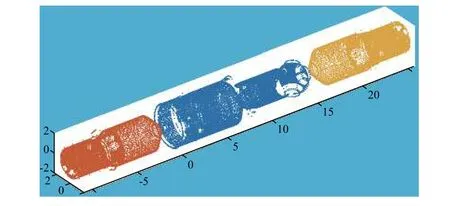
图3 空间站三舱组合体模态综合Fig.3 Modal synthesis for three-cabin combination of space station

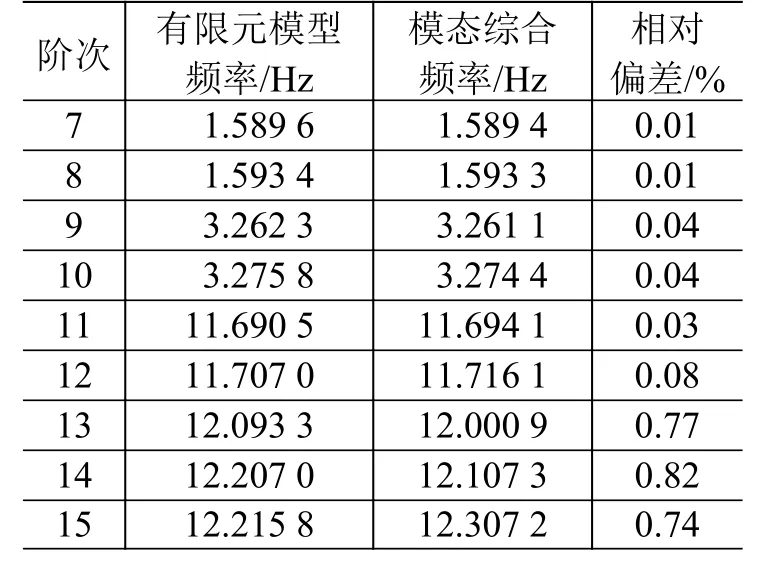
表1 子结构模态综合计算精度Table 1 The calculation accuracy of substructure modal synthesis

4 结束语

本文研究了固定界面模态综合法在复杂空间结构动力学分析中的应用，通过对舱段对接模型的对比分析，验证了其有效性。在实际工程应用中，应注意以下几个问题：

1）根据所要计算的频带范围，选择适当的模态阶数，从而既可保证模态综合模型对原始有限元模型在计算频带范围内的近似精度，也可提高模型的计算效率；

2）尽量控制子结构模型的界面点数量，因为界面点自由度的增多会导致模态综合模型的高阶自由频率的增高，增加微分方程的刚度，显著增大时域响应的计算量；

3）在模态综合法中，可以分别对子结构的模态阻尼和界面阻尼赋值，在模态综合后，系统耦合模型的各阶模态会表现出不同的阻尼比。