预测复杂装备研制费用的GM(0,N)模型

吴利丰，于 亮，文朝霞

(1.河北工程大学管理工程与商学院，河北 邯郸 056038；2.中国运载火箭技术研究院，北京 100076)

1 引言

大型复杂装备是指客户需求复杂、产品组成复杂、产品技术复杂、制造过程复杂、项目管理复杂的一类装备，如航天器、飞机、航空母舰、武器系统等。随着科技飞速发展及其在军事领域的广泛应用，大型复杂装备费用增长在国内外都成为普遍现象。费用成为影响装备发展的首要问题。为有效控制费用增长，提高经费使用效率，准确预测装备各阶段的费用成为重要问题。

由于对复杂装备费用有影响的参数很多，样本较少，刘铭等[1]利用GA和BP融合的算法估算装备费用。Deng和Yeh[2]利用最小二乘向量机方法估算机体机构的制造成本。Curran等[3]利用genetic causal技术估算飞机全寿命周期的费用。Lin等[4]利用一种混合方法估计转子叶片的制造成本。Hart等[5]从系统工程的角度提出一种估算船舶全寿命周期费用的方法。Trivailo等[6]总结了在航空计划的早期阶段，硬件成本估算的方法、模型和工具。文献[7-11] 分别用GM(0,N)模型及其改进模型预测复杂装备的费用。我们建模的目的是为了预测，不仅仅为了拟合，但是文献[7-11]所用的模型没有从理论上证明该方法对提高预测精度有帮助。本文从理论上分析已有GM(0,N)模型的稳定性，提出一种可以充分利用与待预测对象相似数据的GM(0,N)，实例说明了该模型的有效性和实用性。

2 GM(0,N)模型的稳定性分析

相关证明过程见戴华[12]。

由于所有矩阵范数是等价的，不管采用哪种范数，本质上是一致的，为讨论方便，这里取矩阵的m1范数，与之相容的向量范数为向量1范数。

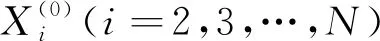
参数的最小二乘估计满足

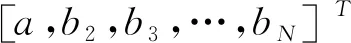
其中

定理2设GM(0,N)模型

参数的解为x，如果只发生扰动

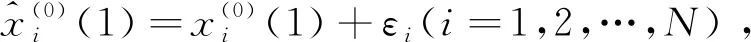
证明:如果只发生扰动

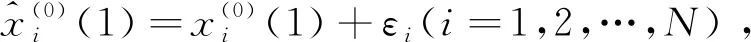
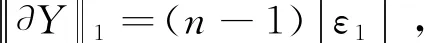
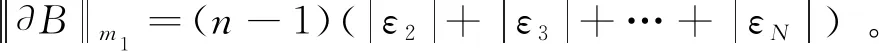
证明：如果只发生扰动

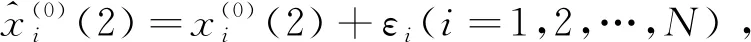
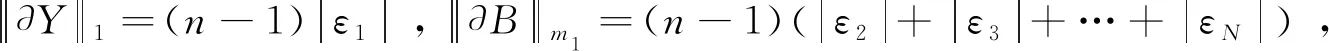
如果只发生扰动

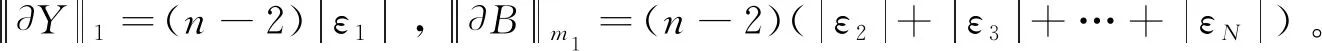
证毕。

3 原始数据序列的排序方法

何莎伟等[7]仅仅数据的增长规律对原始数据排序，但是难以从理论上严格证明这种排序方法对改善模型对未来的预测精度是有帮助的。本文将依据样本相关因素数据与待预测对象相关因素数据的相似度排序。

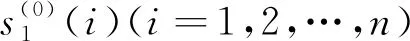
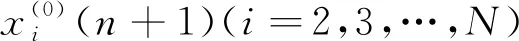
为样本Ai与An+1的相似度，其中

(i=1,2,…,n,j=2,3,…,N)

相似度越小，表示Ai与An+1越相似，如果γp<γq，表示样本Ap比样本Aq更相似An+1。在预测c0时，Ap的权重大于Aq。

定理4若样本的系统数据发生仿射变换，即

样本Ai与An+1的相似度保持不变。

依据相似度排序，数据矩阵第1行的数据是与待预测对象An+1最相似的样本数据，依次排列，第n行的样本数据与待预测对象An+1最不相似的样本数据，最终排列的数据矩阵记为

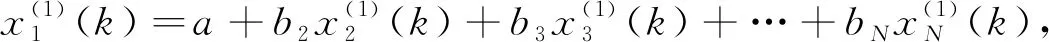
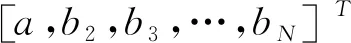
其中

进一步预测待预测对象的费用。

4 实例分析

为便于比较，本文采用刘建[13]的实例。设序号1-7的导弹为样本，预测序号为8的导弹研制费用。拟合精度的比较、预测精度的比较分别见表2、表3。

从表2、3看，无论是拟合精度，还是预测精度，本文模型都明显高于多元线性回归，说明本文模型能够挖掘系统的演化规律。

4 结语

1)由于原始序列样本量较小,解的扰动界较小，所以从扰动界大小的角度看，本文的GM(0,N)模型适合于小样本建模。并不是样本越小模型越好，模型的优劣包括模型的拟合和预测效果、模型的稳定性等。本文只是从稳定性的角度考虑，当样本量较小时，GM(0,N)模型相对稳定。

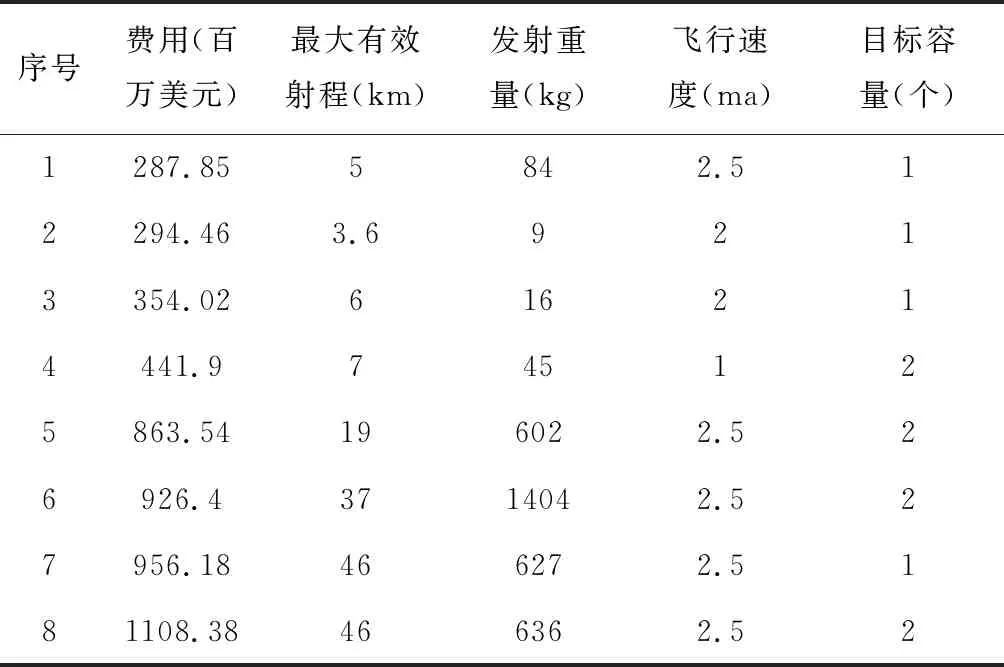
表1 导弹研制费用与性能参数原始数据表

表2 拟合精度比较表

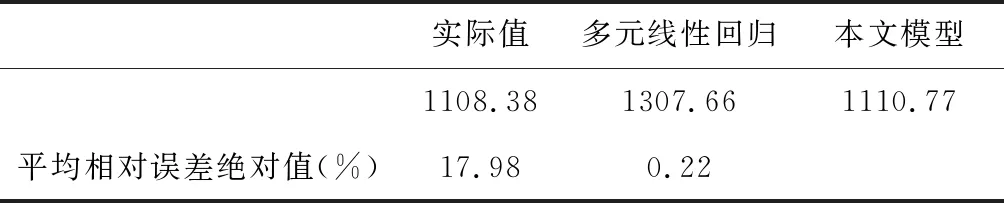
表3 预测结果比较表

如果模型的原始数据完全满足线性关系，样本量再多，模型也是稳定的；如果模型的原始数据完全满足线性关系，也不需要建立GM(0,N)模型，可以建立一般的多元线性回归模型，但是我们经常遇到的数据不一定完全满足线性关系。

2)本文所建GM(0,N)模型中，与待预测对象An+1越相似的样本数据对GM(0,N)模型解的影响越敏感，从敏感性角度说明与待预测对象An+1越相似的样本数据，其影响权重越大。