提高中学生直观想象能力的教学策略研究

濮春秋

(江苏省苏州市苏州大学附属尹山湖中学 江苏 苏州 215000)

1.直观想象的含义

直观想象是指借助空间想象感知事物的形态与变化，利用几何图形理解和解决数学问题。将数学问题以图形的形式呈现出来，通过数与形结合的方式，寻找到解决问题的行之有效之法，提升对数学问题的本质以及发展规律的探索与认识。

直观想象能力是数学素质与数学能力的重要方面，是一种重要的数学思想与方法；重视直观想象核心素养的培养，有利于学生养成运用图形和空间想象思考问题的习惯，有利于学生提升数形结合的能力，有利于学生形成借助图形和空间想象进行分析、推理建构数学体系，论证数学概念的能力。

2.掌握基本图形性质是基础

对基本图形性质的理解是产生直觉的源泉，因此若想在数学教学过程中提高学生的直观洞察力，就得让学生掌握图形的基本性质。在数学教学中，需要时刻锻炼学生的基本功，在函数的部分让学生能熟练掌握基本函数的图像特征与性质，例如在处在初中阶段学习的一次函数、二次函数、反比例函数的性质；在立体几何学部分让学生充分把握相关几何体的性质。通过对基础知识的有效把握，学生在利用图形进行平移、对称等变换时，能激发学生思维，启发学生解决问题的思路。

而在教学中教授基本图形的性质时，一定要着眼于学生现实生活经验，从学生现有知识水平出发，让学生学习这些知识时不用死记硬背，而寻找到更为简易的方法进行记忆。例如在初中阶段中立体几何部分，学生常常觉得几何体的性质与特点复杂，无法进行有效记忆与理解，这是教师就应当通过研究教材与研究学生找到突破点，教师在教学时首先需要将立体几何以直观的形式呈现在学生面前，让学生在感官上感知几何体，然后让学生找到几何体各个要素之间的桥梁。

3.创设数学中“直观洞察力”的意境

想要培养学生的直观想象能力以解决立体几何与解析几何的问题时，我们通常需要做到让学生自己在头脑中进行想象，鼓励他们跟着自己的感觉走，能充分表达自己的直觉感受。在立体几何中面对复杂的图形，经过剖析能找出所需要的图形中点、线、面之间的关系，能在合理位置进行辅助线的添加；在解析几何面对函数问题时，要利用函数图像的特征找到解决问题的思路。

例如在教授异面直线的知识点时，学生可能无法立马了解异面等知识，这时教师可以通过设计将粉笔盒作为情境，看成一个长方体，以实物的形式直观的展现给学生，让学生观察长方体中各条棱之间的位置关系，这样异面直线的定义便一目了然：即不同在任何一个平面内的两条直线叫做异面直线。至此，学生已经了解了异面直线的定义，有了直观的感受，然后就让学生回忆所学的在空间内作平面的方法，引导学生利用手头的尺规与纸笔完成一般化的异面直线。

4.加强文字、图形与符号语言的转化训练

在直观想象中，学会画图与识图是基础，但直观想象能力的核心是“想象”，即通过对空间知觉等材料的分析、加工、抽象概括而产生的新形象的心理过程。我们所说的直观想象中的“想象”的实质是几何语言和几何图形之间的转化。思维与想象是两个密不可分的过程，它们紧密相连，又相互影响。语言则是学生直观想象能力与思维发展的载体。因此，教师需要通过加强文字、符号与图形语言转化的训练来完成直观想象能力与思维能力的培养。

在立体几何的教学中，教师通常要求将所学的定理、公里、定义以文字语言、符号语言和图形语言的方式分别表示出来，以训练学生三种语言的转换能力。

在平面几何题目的教学中，有时练习题中只展示了文字语言的表达而不给出学生图形，这时，学生就需要通过自己的理解将文字语言翻译成符号语言，根据题目文字叙述自己画出图形再进行分析探索解决问题。

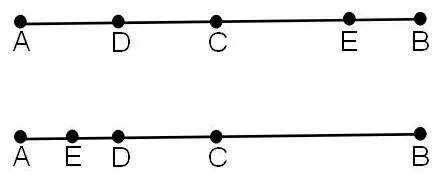
例：已知线段AB=84cm，C是线段AB的中点，D是线段AC的中点，点E在线段AB上，且CE=BC，求DE的长度。

从题目分析我们可以发现，题目中所给的“线段AB=84cm，C是线段AB的中点，D是线段AC的中点”这三个条件我们可以画出一条包含四个点的线段，但是在学生结合题目中另一个条件时，就需要学生通过直观的想象将点E同线段进行动态的移动，使得满足CE=BC，最终发现这样的线段不唯一，如图，点E可能分布于点C左右两侧，因此需要分类讨论。

因此教师在进行几何课程的教学中，要注重学生直观思维与抽象思维之间的转化，培养学生的动态直观想象能力，在设计题目时应有利于发挥学生的想象力，提升学生自我反思的能力的同时培养他们的转化与化归的思维。

5.通过图形的运动变化来培养学生的直观想象能力

当学生可以从情境中想象出空间图形的运动与变化时说明学生的直观想象能力进入了一个更深的层次。教师需要挖掘一些教材中运动变化的素材，经过反复钻研课本教材后，利用多媒体工具制作，加深素材的直观性，在引导学生总结归纳的过程中培养学生的直观想象能力，促进学生思维的发展。让学生学会利用图形运动与变化的观点解决问题，将学生的主体地位在课堂上得到体现，提高课堂学习兴趣，完善课堂学习目标。

加强学生对图形运动变化的识别训练有助于减少因图形的运动以及学生思维发展的不充分性而给他们思维上带来的某些障碍，让学生能更进一步理解和认识空间图形的本质，将代表视觉符号的几何图形与表象相结合，是学生理解数学模型的关键所在。

6.结语

直观想象力的培养是培养数学理解能力的基本途径，在数学教学中，教师要努力做到将培养学生直观想象能力贯穿于学生思维发展的始末，结合实际情况，对于学生之间存在的阶段与个体差异探索有针对性教学对策，旨在提升中学生整体的直观想象能力。