考虑多阶段决策信息集结的新算法及其应用
李静,张玉林
(东南大学经济管理学院,江苏南京211189)
0 引 言
实际问题的决策中,客观世界的不确定性、人类思维的模糊性以及实际决策问题的复杂性,都会令决策信息无法用精确数表示。由于时间紧迫、缺乏数据以及专业知识有限,决策者常常无法提供精确的评价值,只能提供不确定性意见。为此,ZADEH[1]提出了模糊集的概念,并将其运用于决策理论研究,随后该理论及其应用方法迅速发展[1-2]。其中,多属性决策问题一直是决策理论研究的重点,决策者的偏好或评价信息往往以区间数的形式表示。相关研究主要集中在属性权重已知、部分已知或未知以及不完全信息等情形,已有较多学者对相关问题进行探索并取得了一定成果[3-10]。
也有部分学者在静态综合评价的基础上考虑时序动态综合评价问题,在多阶段信息集结方面进行深入研究[11]。 如 XU等[12]在直觉模糊信息情形下研究动态多阶段决策问题,提出了2种有效的加权算子;张发明等[13]针对目前多阶段交互式评价问题,在考虑评分区间与可变评价信息内在联系的基础上,提出一种基于新的多阶段群决策方法;卢志平等[14]针对阶段赋权的三端点区间数型群决策问题,提出一种属性和专家权重计算方法;李欢等[15]基于累积前景理论,提出一种考虑三参照点的风险型动态决策方法,并通过投资公司的选择案例验证了其有效性。通过梳理以往多阶段决策研究的相关文献,发现考虑信息内在联系的相关研究较多,而对多阶段群体信息集结方法的相关研究较少,已有的集结方法主要有徐泽水[16-17]提出的动态权重集结算子(DWA)、多阶段语言信息集结的DLGW算子以及刘勇等[10]提出的灰色关联分析方法。
对于多阶段的决策问题,其重点在于评价信息的集结处理,目前已有的信息集结方法在集结多阶段信息时各有优势,多为对评价信息进行平均或加权平均,集结结果未能达到帕累托最优。近年来,一些学者将植物模拟生长算法(PGSA)用于信息集结并取得了良好效果。LI等[18]运用植物模拟生长算法求解多属性区间数集结问题,并采用算例验证该方法的有效性。LIU等[19]基于植物模拟生长算法集结多属性区间数矩阵,研究了专家的综合权重确定问题。李磊等[20]将该算法运用于处理AHP专家判断矩阵的集结问题,取得了良好效果。 QIU等[21]将PGSA用于区间直觉模糊信息的求解,李磊等[22]运用PGSA处理非确定语言信息群决策问题并验证了其有效性。上述学者的研究表明,PGSA在信息集结方面具备合理性,但少有学者将其应用于多阶段群决策问题的处理。鉴于此,本文将植物模拟生长算法应用于多阶段信息的集结问题,针对多阶段评价问题中属性评价值以区间数表示的情形,基于区间信息离差最小化的思想,将区间评价值转化为坐标系中的二维坐标点,构建离差最小化信息集结模型,通过实际建模和编码求解得到各属性阶段评价集结值,有效解决了多阶段评价信息集结问题。最后,将其应用于物流服务商的多阶段绩效评价,验证了该方法是可行且有效的。
1 预备知识

称D(a ,b)为区间数a,b的离差。D(a ,b)越大,区间数a,b的离差越大。
定义3 设
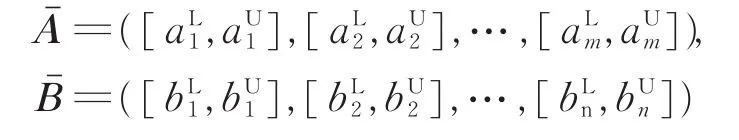
为2个正闭区间数型向量,令


称D(A,B)为区间型矩阵A,B的离差。
The sun goes down without twilight, rain or snow will come next.
定义5 设区间数离差最小化的理想解为A*=

称A*为离差最小化的区间集结矩阵。
定义6 正闭区间数型矩阵中,属性规范化方法如下[24]:
对于效益型属性,令

对于成本型属性,令


2 阶段赋权的多阶段信息集结模型
2.1 问题描述
对于多阶段群决策问题的处理,核心在于集结多阶段评价信息,进而得到综合评价值。评价对象组成的集合为S=(s1,s2,…,sn),对象的属性集A=(a1,a2,…,an),评价阶段集 T={ }1,2,…,p。对象i在第k阶段对属性aj的评价值为akij,由于实际决策问题的复杂性,指标属性值往往不是具体的精确数,而以区间数形式给出,记为其中akLij和akUij分别为属性值的上限和下限为第k阶段j属性的权重,为阶段权重,和均已知,且
2.2 区间数的映射
为便于集结多阶段评价属性的区间数,采用将各阶段的属性区间数映射到二维坐标系的方法[24]。 将各评价对象的属性区间数k映射为二维坐标系中的点集,即
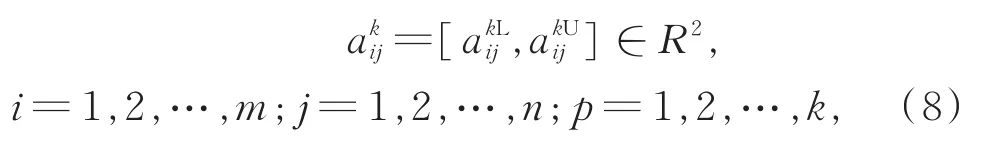
式(8)中,R2为二维欧式空间。
2.3 基于植物模拟生长算法的离差最小化集结点的求解
将专家偏好区间信息的集结转化为离差最小化集结点的求解问题。针对多个区间数的信息集结问题,实际上是NP难题。为寻找理想解,本文选取模拟植物生长算法(PGSA)进行NP问题的求解。模拟植物生长算法(plant growth simulation algorithm,PGSA)由李彤等[25]于 2005年创立,该算法以植物向光性机理为启发式准则,有效处理全局优化问题。PGSA法,定义生长点,按照东南西北4个方向生长,产生新枝,设新枝的旋转角∂为90°,将枝干的长度设定为l/1 000,l为有界闭箱的长度,本文求解离差最小化集结点的具体步骤如下:
Step1 构建赋权的多阶段信息集结模型:
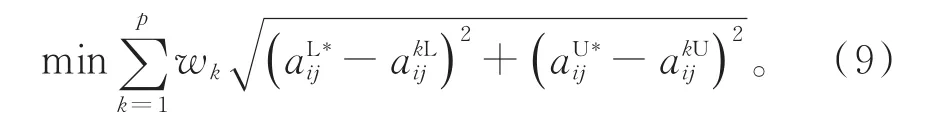
Step2 利用植物模拟生长算法求解模型(9),得到离差最小化集结矩阵,具体步骤如下:
Step2.1 选择初始生长点am∈X,X为R2中的有界闭箱,初始生长点am为有界闭箱内随机均匀分布的点,数量为h;
Step2.2 求解各生长点的生长概率

Step2.3 在闭区间[ ]0,1上随机生成一个值,根据上述结果选定各生长点的概率空间,并以随机数来选择迭代生长点am;
Step2.4 确定步长λ(一般取l/1 000),生长点am按照∂=90∘的L-系统生长,然后用新的生长点替换am;
Step2.5 如果不再有新枝产生,则停止运算,否则转步骤2.2。
Step3 基于式(5)和式(6)对集结矩阵A*进行规范化处理,得到规范化判断矩阵。
Step4 根据式(7)求解综合评价值并进行排序。
3 案例分析
以文献[23]中第三方逆向物流服务商(3PRLPs)选择为例,即某制造公司邀请专家对5个第三方逆向物流服务商以往及现在(4个决策阶段)的7个属性的绩效进行评价,进而选择合适的第三方逆向物流服务商(3PRLP)。专家对第三方物流服务商多阶段的评价值如表1所示,各阶段各属性权重如表2所示,其中决策阶段的时段权重为vt=(0.3,0.2,0.2,0.3),集结后和无量纲化处理后各属性综合评价值见表3和表4。
各服务商的综合评价值如表5所示。

表1 各阶段下3PRLPs的评价值Table 1 Evaluation values of 3PRLPs at different stages
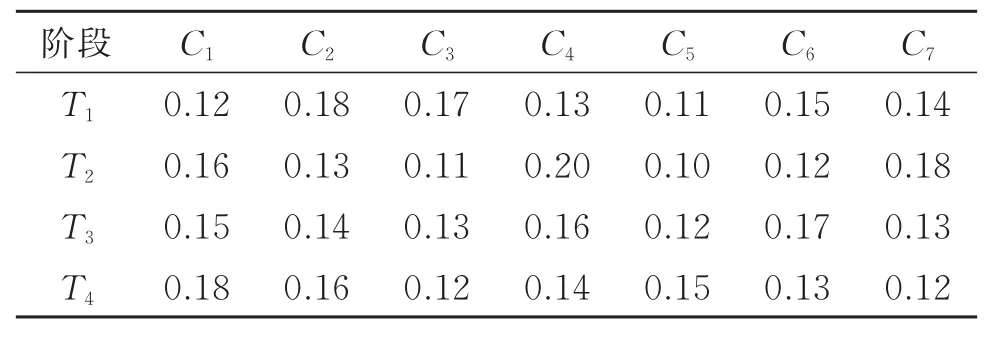
表2 各阶段下的属性权重Table 2 Attribute weights under different stages

表3 集结后各属性综合评价值Table 3 Comprehensive evaluation values of attributes after aggregation
运用本文方法得到的评价结果为:3PRLP2>3PRLP4>3PRLP5>3PRLP3>3PRLP1,文 献[23]得到的评价结果为3PRLP2>3PRLP3>3PRLP5>3PRLP4>3PRLP1。从评价结果看,2种方法中最好和最差供应商一致,排名在中间的结果不同。对比来看,2种方法均对数据进行了无量纲化处理,但本文考虑最小化集结矩阵与阶段区间矩阵之间的距离,集结结果更趋于帕累托最优,最终评价值更符合多阶段评价的目标。
4 结 论
提出了一种解决属性值为区间数的多阶段区间决策信息集结问题方法。该方法考虑最小化集结矩阵与阶段区间矩阵之间的距离,寻求更趋近于帕累托最优的集结结果,使最终评价值更符合多阶段评价的目标。首先,将各阶段区间评价信息转化为坐标系中的二维坐标点,然后,构建离差最小化模型,并运用植物模拟生长算法进行编码求解,最后,通过实际案例验证该方法是可用和合理的。新方法易于计算机实现,可广泛运用于多阶段评价问题的信息集结求解。

表4 无量纲化后各属性综合评价值Table 4 Comprehensive evaluation value of each attribute after dimensionless analysis

表5 各服务商综合评价值Table 5 Comprehensive evaluation value of service providers

