正规Bihom--Lie代数的上边缘算子刻画

熊桢

（宜春学院数学与计算机科学学院，江西宜春336000）

0 引 言

文献［1］引入的Bihom-Lie代数结构，是Hom-Lie代数结构的推广。Hom-Lie代数结构在数学和物理中有重要的应用［2-4］，引起了越来越多学者的关注和研究，文献［5-8］系统研究了Hom-Lie代数的表示理论、上同调理论和同调理论，其中，文献［8］给出了Hom-Lie代数表示的定义以及边缘算子，文献［7］给出了Hom-Lie代数的上边缘算子和上边缘链，计算了上边缘算子所对应的上同调群并讨论了Hom-Lie代数的形变。 文献［9］研究了正规Bihom-Lie代数(L,[⋅,⋅],α,β)的表示，并在部分上链（Bihom cochain）上给出了表示所对应的上边缘算子。对于平凡表示，文献［9］考虑部分上链并在Ckα,β(L)上给出了相对于平凡表示的上边缘算子。

定理1 设L是向量空间，2个可逆映射α,β：L→L均是线性的并满足α∘β=β∘α。 如果存在算子且满足：

下面介绍Bihom-Lie代数的相关概念和结论。

定 义 1［4］（i）Bihom-Lie 代 数 为 四 元 组其中 L 为向量空间均为线性映射，对于任意的满足：

1 上边缘算子的定义和性质

命题1 d是上边缘算子，有d∘d=0。

同理可知，(9)+(12)=0，(10)+(11)=0，则有d∘d=0，从而命题获证。

另一等式可类似证得，所以命题2得证。

命题3 对任意的有

因此，当k=1时，有

用归纳法，假设当k=n时，下式成立：

则对任意的 ω ∈ L*，ξ∧ ω ∈ ∧n+1L*，有

从而完成了证明。

2 主要定理的证明

定理1的证明 根据引言和上边缘算子的性质,定理的后半部分显然成立，所以只需证明定理的前半部分。

那么，

从而有

第2步 由条件（ii），

从而有

同理, 有

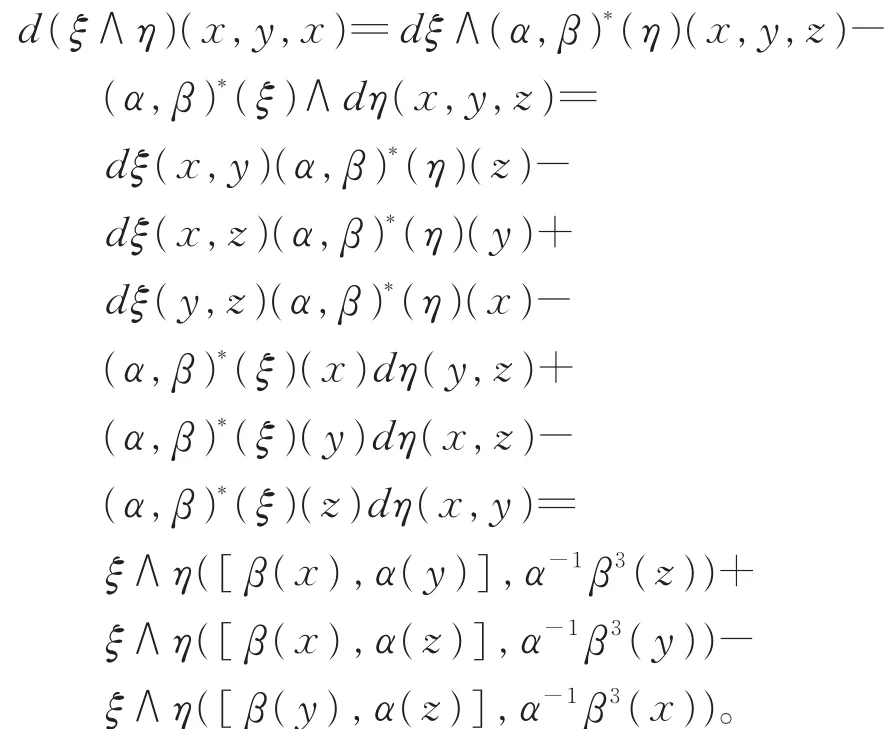
从而有

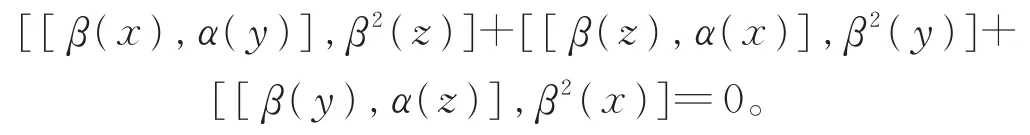
定理证毕。