GRCA（1）模型中误差方差自加权估计的渐近分布

傅可昂，丁丽，李婷，陈豪，何文凯

（浙江工商大学统计与数学学院，浙江杭州310018）

0 引 言

设{yt}为一阶自回归时间序列模型：

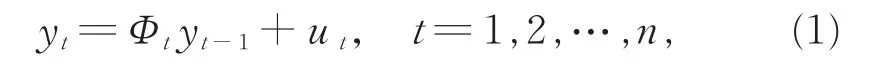
其中，yt为 t时刻的观测值，Φt为随机系数，ut为随机误差，且为满足的独立同分布随机向量序列。由于允许和ut相依，故模型(1)常被称为一阶广义随机系数自回归(GRCA(1))模型。当与ut相互独立时，模型(1)为一般的随机系数自回归模型；当时，模型(1)为一阶常系数自回归模型。由于模型(1)能较好地描述工程动力系统和经济数据的波动，近年来广受学者的关注，如HWANG等[1-2]考虑了参数估计的渐近分布；CARRASCO等[3]研究了模型的高阶矩性质；ZHAO等[4]利用经验似然方法构建了参数的置信区间；赵志文等[5]给出了最小渐近方差下的参数估计；ZHAO等[6]考虑了模型中随机系数的常数化检验；ZHAO等[7]考虑了模型的变量选择问题。

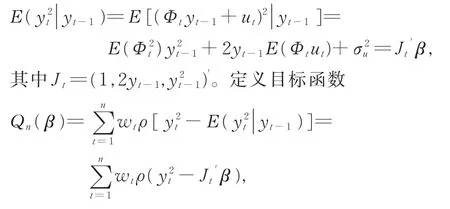
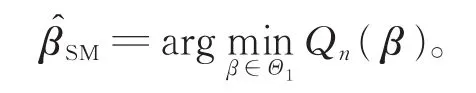
为了给出自加权M-估计的渐近分布，需要以下假设条件：

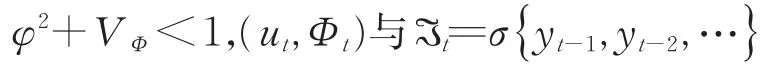
假设 1相互独立。

数据全面 应用广泛 共享顺畅（施继业） ........................................................................................................5-14

假设5其中g(x)是实数域上一正函数,满足

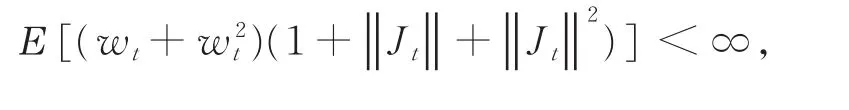
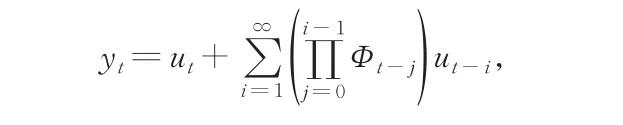
其中的无穷级数依概率和L2范数收敛[1]，故假设1常被用于平稳GRCA模型的参数估计。假设2～假设4是处理M-估计时常用的标准假设，很多函数均满足这些条件，例如其中z值待定，此时对应的估计分别称为自加权二乘估计、自加权Huber估计；若ρ函数不可微但存在左右导数和，则可选择一函数满足，本文直接假设函数存在一阶导数。假设5给出了本文的矩要求，通过调节，降低了文献[1，8]中矩的要求，关于的选取可见文献[10-11]。

接下来，给出GRCA(1)模型中方差向量的自加权M-估计的渐近分布。

定理1 对于模型（1），在假设1～假设5成立的条件下，有

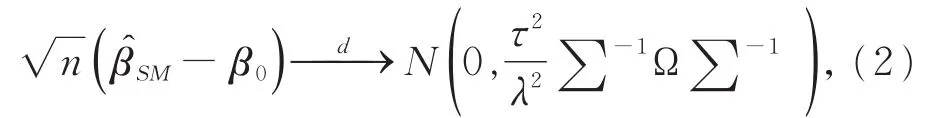
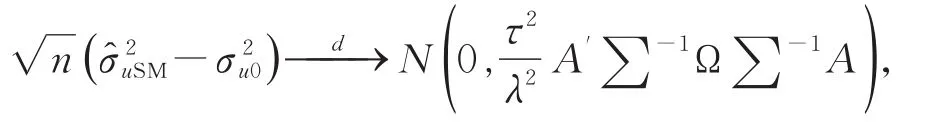
1 数值模拟

本节将对β的自加权M-估计进行有限样本的模拟研究，主要比较条件二乘估计(LS)与自加权二乘估计(SM1)、自加权Huber估计(SM2)这两类自加权M-估计。

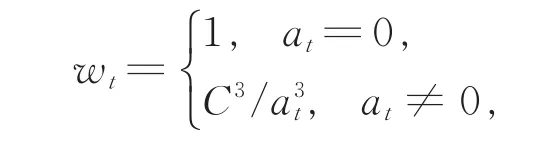
在模拟时,当ut～N(0,σ2)时 ，分别取(,r,)=(0.5,0,1)，(0.7,0.1,1)，(0.5,0.5,1)，也 就 是 β 为(1,0,0.25)，(1,0.1,0.5)，(1,0.5,0.5)；当 ut～t(3)时，分别取 (φ,r)=(0.5,0)，(0.7,0.1)，(0.5,0.4)，即为(3,0,0.25)，(3,0.3,0.52)，(3,1.2,0.73)。 在 样 本 容量为200，500和1 000时，分别重复运行1 000次，观察条件二乘估计与自加权估计的均值，具体结果见表1和表2。

由表1和表2的数据可知，总体而言，条件自加权估计优于条件二乘估计，尤其是当真值为(1,0.5,0.5)和(3,1.2,0.73)时，条件二乘估计的结果已偏离可以接受的范围，而条件自加权估计仍较接近真值。

2 定理的证明

首先，介绍3个均在定理1条件下构建的引理。

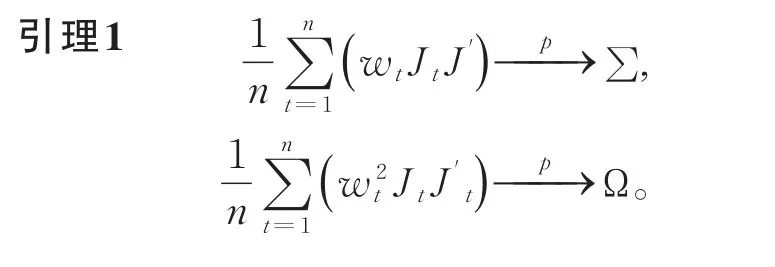
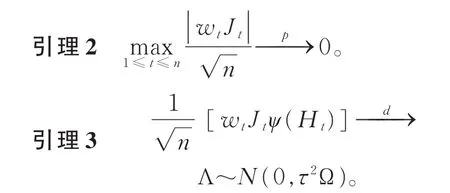
由假设4和假设5,再结合平稳遍历性,即得引理1成立。由平稳性和正项级数收敛性质即得引理2成立。故此处只给出引理3的详细证明。

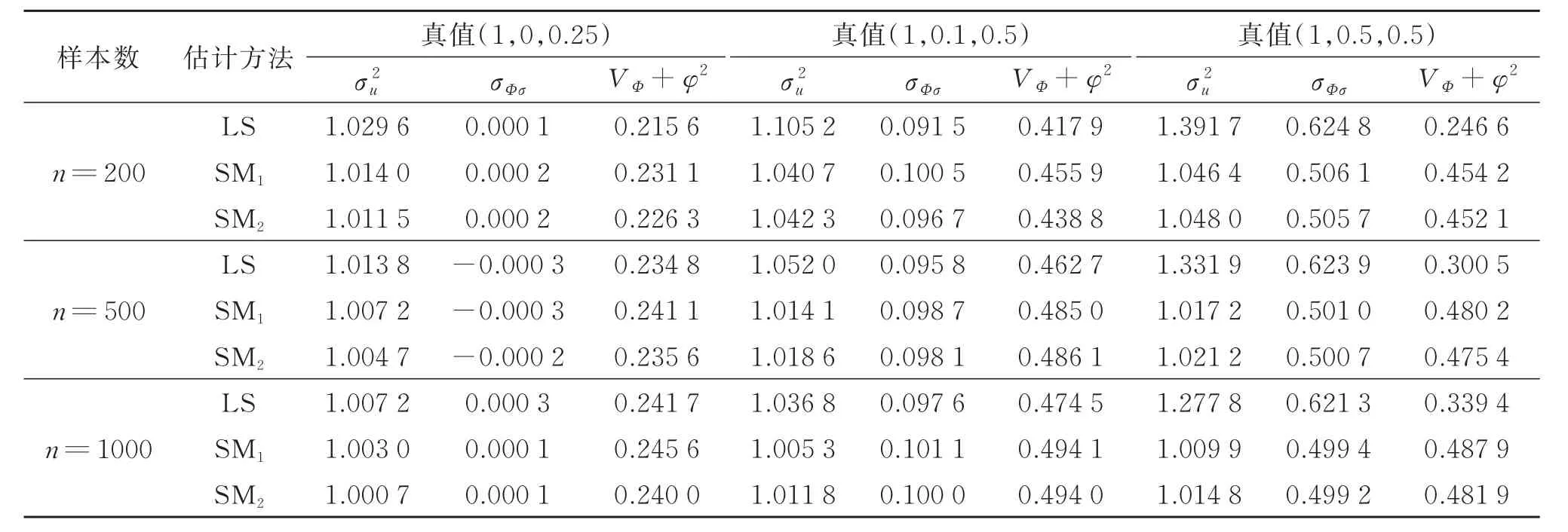
表1 ut～N(0，σ2)时的模拟结果Table1 The simulation results withut～N(0，σ2)

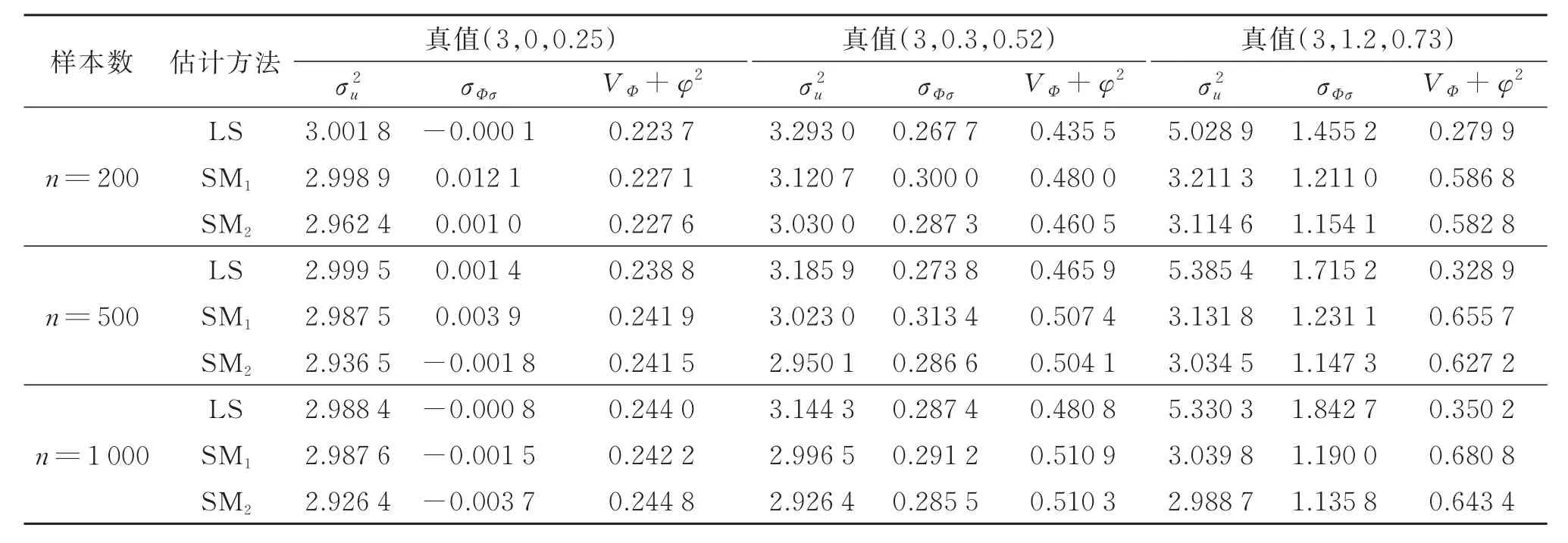
表2 ut～t(3)时的模拟结果Table 2 The simulation results withut～t(3)

因为Vn(μ)有凸的样本路径,表明不同路径下收敛一致,V在处有唯一的最小值，故由文献[12]中的引理2.2可得

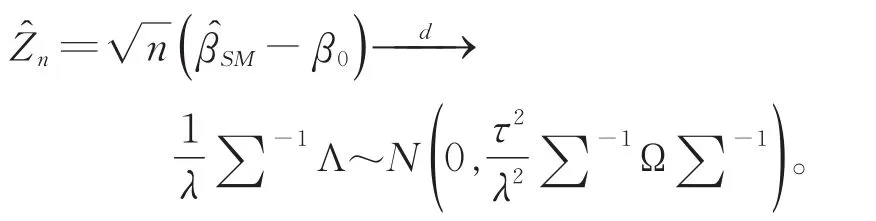
定理证毕！