图的Aα-特征多项式系数的一个注记.浙江大学学报(理学版),2019,46(4):399⁃404
柳顺义,覃忠美(长安大学理学院,陕西西安710064)
0 Introduction
LetG=(V(G),E(G))be a graph with vertex setV(G)=and edge setE(G).The adjacency matrix ofG,denoted byA(G)=(aij),is an n×n symmetric matrix such that aij=1 if vivj∈E(G)andaij=0otherwise.Letdi=dG(vi)be the degree of vertexviinG.The degree matrix ofG,denoted byD(G),is the diagonal matrix with diagonal entries the vertex degrees ofG.The Laplacian matrix and the signless Laplacian matrix ofGare defined as L(G)=D(G)-A(G)andQ(G)=D(G)+A(G),respectively.
NIKIFOROV[1]proposed to study the following matrix

The spectral radius of Aα(G) has been investigated and some extremal results were obtained[2-4].NIKIFOROV et al[5]studied the positive semidefiniteness ofAα(G).CARDOSO et al[6]gave a characterizationonthemultiplicityofαasan eigenvalue ofAα(G)in terms of the numbers of the pendant and quasi-pendant vertices of a graphG.For more onAα(G),we refer the reader to[1].
LetG be a graph onnvertices.TheAαcharacteristic polynomial ofG is defined as the characteristic polynomial ofAα(G),i.e.,whereInis the identity matrix of sizen.

We can write theAα-characteristic polynomial φ(Aα(G);x)in the coefficient form

For many graph polynomials,it is of interest to investigate the properties of their coefficients.In particular,we hope to get the algebraic expressions for the coefficients of graph polynomials.For example,OLIVEIRA et al[7]gave the algebraic expressions for the first four coefficients of the Laplacian characteristic polynomial of a graph.CVETKOVIC et al[8]gave the algebraic expressions for the first three coefficients of the signless Laplacian characteristic polynomial of a graph.WANG et al[9]gave the algebraic expression for the fourth coefficientofthe signless Laplacian characteristic polynomial of a graph.GUO et al[10]obtained combinatorial expressions for the fifth coefficient of the(signless)Laplacian characteristic polynomial of a graph.
LIU et al[11]formulated the first four coefficients of theAα-characteristic polynomial of a graph,and computed the firstfourcoefficients ofthe Aαcharacteristic polynomials of some specific graphs.
Theorem 1[11]LetGbe a graph withnvertices and m edges, and let(d1,d2,…,dn)be its degree sequence.Suppose that

Then

and

In this paper, we obtain a combinatorial expression for the fifth coefficientcα4(G)of theAαcharacteristic polynomial of a graphG.Here and subsequently,we usetGandqGto denote the number of triangles(i.e.,cycles of length 3)and quadrangles(i.e.,cycles of length 4)ofG,respectively,and tG(v)denotes the number of triangles containing the vertexvofG.
Theorem 2 LetGbe a graph withnvertices andm edges,and let(d1,d2,…,dn)be its degree sequence.Suppose that

Then

The rest of the paper is organized as follows.In section 1,we give some basic results which will be used to prove theorem 2.In section 2,we present a proof of theorem 2,and calculate the fifth coefficient cα4(G)of theAα-characteristic polynomials of some specific graphs as examples.
1 Lemmas
It is well known that the characteristic polynomial of a square matrix can be obtained by computing the traces of the powers of the matrix.Recall that the trace of ann×nmatrixM=(aij)is the sum of the elements on the main diagonal ofM,i.e.,tr(M)=a11+a22+…+ann.
Lemma1[12]LetMbe a square matrix of sizen.If det(xIn-M)=aixn-i, then a1=-t1, and kak=-tk-a1tk-1-…-ak-1t1,k=2,3,…,n,wheretkis thetraceofMk.
Lemma1 plays an important role in section 2 where we obtain the first five coefficients of theAαcharacteristic polynomial.
The following results present the basic properties of the trace.
Lemma2[13]LetAandBbe twon×nmatrices,and letcbe a complex number.Then

Lemma3[13]IfAis anm×nmatrix andBis an n×mmatrix.Thentr(AB)=tr(BA).
More generally,the trace is invariant under cyclic permutations.
Lemma4 LetA1,A2,…,Anben× nmatrices.Then

Since matrix multiplication has the associative property,Lemma4 is an immediate consequence ofLemma3.For example,

ByLemma4,we have

It should be noted that, in general,tr(ABC)≠tr(ACB).However,if products of three symmetric matrices are considered,any permutation is allowed.
Lemma5 LetA,BandCbe threen×nsymmetric matrices.Then

Proof SinceA,BandCare all symmetric,we have AT=A,BT=B,andCT=C.Thus,byLemmas 2(3)andLemma3,

In the same manner,we can see that the other equalities hold.
The following result gives the algebraic expressionsforthe trace ofthe powersofthe adjacency matrix of a graph.
Lemma6 LetGbe a graph withnvertices andm edges,andAbe the adjacency matrix ofG.If the degree sequence ofG is (d1,d2,…,dn), then wheretGandqGdenote the number of triangles and quadrangles ofG,respectively.

The proof ofLemma6 is based on the wellknown result:The(i,j)-entry of the matrixAkis equal to the number of walks of lengthkthat starts at vertexviand ends at vertexvj.The details are left to the reader.
2 Coefficients
In this section,we present a proof of theorem 2.As an application,we obtain the explicit expressions for the fifth coefficientcα4(G)ofAα-characteristic polynomials of some specific graphs.
2.1 Proof of theorem 2
In this subsection,we give the proof of theorem 2.The basic idea of the proof is to useLemma1 recursively.
Proof LetAα:=Aα(G),A:=A(G),andD:=D(G).Suppose thatdet(xIn-Aα)=Let tkbe the trace ofAkα.ByLemma1,we havecα1=-t1,and
Clearly,tr(D2)=It is easy to verify that tr(AD)=tr(DA)=0.ByLemma6,wehave tr(A2)=2m.It follows fromLemma2 that

By eq.(1),we have

Calculating the cubeA3α,we have A3α=(αD+(1- α )A)3= α3D3+ α2(1- α )DAD+

Clearly,tr(D3)=FromLemma5 and by calculation,we have

ByLemma6,we havetr(A3)=6tG.Thus

It follows from eq.(1)that

Calculating the fourth powerA4α,we have


FromLemma5 and by calculation,we have

wheretG()is the number of triangles containing the vertexofG.Thus

It follows from eq.(1)that

This completes the proof.
It is worth pointing out that the proof of theorem 2 also gives a new simpler proof of theorem 1.
Denote by λ1(Aα(G)),λ2(Aα(G)),…,λn(Aα(G))the eigenvalues ofAα(G).NIKIFOROV[1]obtained two explicit expressions for the sum of the eigenvalues of Aα(G)and for the sum of their squares.
Proposition 1[1]LetGbe a graph withnvertices andmedges,and let(d1,d2,…,dn)be the degree sequence ofG.Then
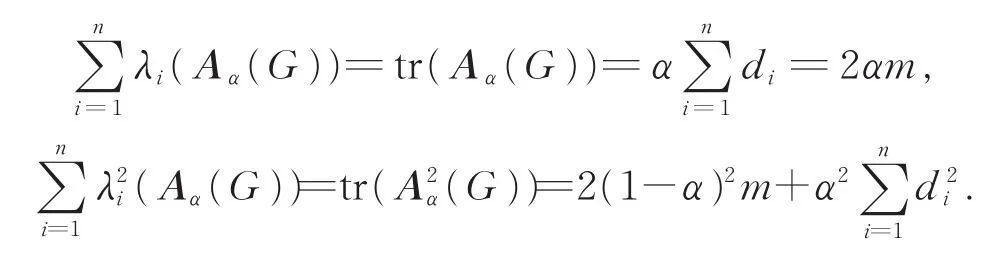
LIU et al[11]gave an expression for the sum of the cubes of the eigenvalues ofAα(G).
Proposition 2[11]LetGbe a graph onnvertices,and let(d1,d2,…,dn)be the degree sequence ofG.Then

By eq.(2),we can immediately obtain a similar expression for the sum of the fourth power of the eigenvalues ofAα(G).
Proposition 3 LetGbe a graph onnvertices,and let(d1,d2,…,dn)be the degree sequence ofG.Then

2.2 Examples
In this subsection, applying theorem 2,we obtain the fifth coefficient cα4(G)of the Aαcharacteristic polynomials of some specific graphs:paths,cycles,complete graphs,complete bipartite graphs,star graphs,and wheel graphs.
Example 1 LetPn(n≥3)be the path onnvertices.We see at once thattPn=qPn=0,andtPn(v)=0for each vertexvofPn.By theorem 2,we have

Example 2 LetCn(n≥5)be the cycle onnvertices.We see at once thattCn=qCn
=0,andtCn
(v)=0for each vertexvofCn.By theorem 2,we have

Example 3 LetKn(n≥4)be the complete graph onnvertices.It is easy to check that

for each vertexvofKn.By theorem 2,we have


Example 4 LetKa,b(a≥b≥2)be the complete bipartite graph with partition sets of sizesaandb.We see at once thattKa,b=0,

andtKa,b()=0for each vertexvofKa,b.By theorem 2,we have
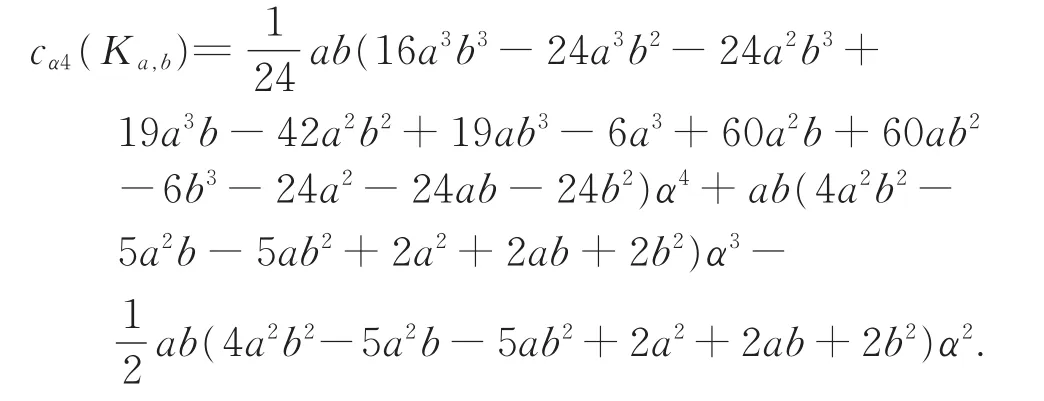
Example 5 LetSn(n≥3)be the star graph with n+1vertices andnedges.We see at once thattSn=qSn=0andtSn(v)=0for each vertexvofSn.By theorem 2,we have

Example 6 LetWn(n≥5)be the wheel graph with n+1vertices and2nedges.It is obvious thattWn=qWn=n.Letv0be the hub(i.e.,the vertex of degreen)of Wn.We see thattWn(v0)=n and tWn(v)=2 for other vertices v of Wn.By theorem 2,we have


