有关矩阵广义逆A(T2,)S的惯性指数及其应用.浙江大学学报(理学版),2019,46(04)：395-398,404

吴中成，贺宁馨（.上海工程技术大学数理与统计学院，上海060；.贵州师范大学数学科学学院，贵州贵阳 55000）

0 Introduction

Throughout this paper,we denote the set of all m×nmatrices over the complex number fieldbym×n,the set of all complex Hermitian matrices of ordermbyHm,thendimensional vector space overbyn.The symbolsA∗,r(A),R(A)andN(A)stand for the conjugate transpose,the rank,the range,and the null space of a matrixA,respectively.IfA∈Hmis positive definite, positive semidefinite, negative definite and negative semidefinite,respectively,we writeA>0,A≥0,A＜0andA≤0.

Recall that an out inverse of a matrixAwith prescribed range spaceT and null spaceS is a solution of the restricted matrix equation

and is denoted byA(2)T,S.Note that the frequentlyused generalized inverse,such as the Moore-Penrose inverse,the weighted Moore-Penrose inverse,the Drazin inverse,and the(generalized)Bott-Duffin inverse of a matrixAare all special cases ofA(2)T,S.Therefore, itis very meaningfulto investigate properties ofA(2)T,S.In the past few years,extensive research has been made related toA(2)T,S.For more details,see[1-4]and the references therein.

wherei+(A),i-(A)andi0(A)are numbers of the positive,negative and zero eigenvalues ofAcounted with multiplicities,respectively.The inertia divides the eigenvalues of the matrix into three parts on the real line.Therefore,it can be used to characterize definiteness of the Hermitian matrix.

In this work,we aim to establish the inertia formulae forandAs applications,we study the definiteness of some matrices.

1 Main results

We begin with the followingLemma,which follows from the definition ofthe inertia ofa Hermitian matrix.

The followingLemmais due to[5].

The followingLemmais needed in what follows.Lemma3[1]SupposeA,r(A)=r,Tis a subspace ofof dimensions≤r,andSis a subspace ofof dimensionm-s,thenAhas a{2}-inverseX such thatR(X)=T,N(X)=Sif and only if

in which caseXis unique and is denoted byA(2)T,S.

From[1],we can get the following result.Lemma4 LetA∈，r(A)=r,letTbe a subspace ofof dimensions≤r,andSbe a subspace ofCCmof dimensionm-ssuch thatA(2)T,Sexists.ThenA(2)T,Sif and only ifT=S⊥,whereS⊥stands for the orthogonal complementary ofS.

Proof If：Let the columns ofUbe a basis forTandS⊥,that isR(U)=TandN(U*)=S.Then the columns ofAUspanAT.It follows from(1)inLemma3 thatr( )AU =s.SupposeU*AUx=0,thenAUxN(U*)=SandAUxR(AU)=AT.A further consequence of(1)isATS=0,thusAUx=0.In view of the fact thatAUis of full column rank,thenx=0,which impliesU*AUis nonsingular.SettingX=U(U*AU)-1U*,we have Xand

Only if：SupposeX=A(T2,)S.Note the fact(R(X))⊥=N(X*),thenT=S⊥immediately.

Now,we give the main results of this paper.Theorem 1 LetAj∈，r(Aj)=rj,letTjbe subspaces ofof dimensionssj≤rj,andSjbe subspaces ofof dimensionsm-sandT=S⊥jjjsuch thatexist.Supposethen there exist(j=1,2,…,n)such that

where

and

Proof From the proof ofLemma4,there exists U1such that

where

Applying (a2)inLemma2 to (6), (7)and simplifying by elementary block congruence matrix operations yield(2)and(3),whereJ1andJ2can be expressed as(4)and(5).

In theorem 5,letA1=-A,A2=BandB1,B2be identity matrices with appropriated size andD,Ai,Bi(=3,4,…,n)vanish.Together with(d1)inLemma1,we can easily get the following corollary.Corollary 1 LetA,B,Tj=Sj⊥be subspaces ofsuch thatA(T2)1,S1,B(T22),S2exist.Then there existUjj(j=1，2)such that

where

and

then

and

Applying (c1)inLemma1 to the following equality

whereIm,Instand for the identity matrices of orderm andn,respectively,then

Combining(10),(11),(13)andLemma2,lead to

Substituting the following equality

into(14)and usingLemma2 and(e1)inLemma1,we can get(9).

2 Applications

In this part,we study the definiteness of some matrices.Theorem 3 LetAj,Tj,Sj,Bj,Uj,D,J1,J2be as in theorem 1.Then

Proof In view of(2),(3)and(a1),(b1)inLemma1,we can easily get the results(a)～(d).

Similarly,we can get the following results.Theorem 4 LetA,B,Tj,Sj,Uj,J3be as in corollary 1.Then

and only if

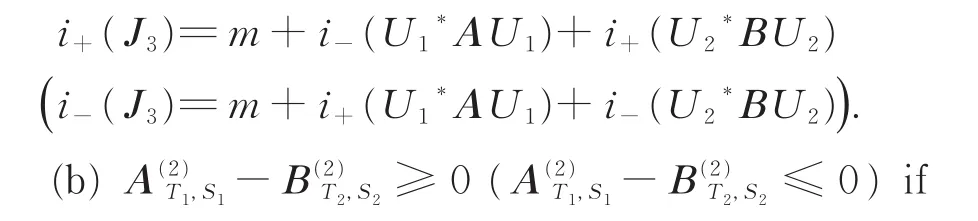
and only if

Theorem 5 LetA,B,D,P,T,S,Uj,andJbe as in theorem 2.Then

only if

3 Conclusion

In this paper,we firstly present the inertia formulae forand the corresponding results are generalized to the situationThen,we consider the inertia formulae forAs applications,we consider the necessary and sufficient conditions forthe matrix expressions mentionedabove and the expression to be positive(semi-)definite and negative(semi-)definite,respectively.