初中数学数形结合思想教学研究与案例分析
陈李梅
摘 要:伴随新课改的全面实施,更注重对学生学科素养的培养。初中数学不仅体系性强、知识面广范,在学习过程中对学生的思维能力也提出了新的要求和更高标准。为了在知识传授中促进学生更好的理解,教师应注重以数形结合思想进行教学研究,一方面培养学生良好的数学核心素养;另一方面以促进学生能够运用所学,分析、思考、解决现实问题,使其具有理性思考的能力及求真务实的学习精神。基于此,笔者结合自身实践,立足于对数形结合思想在初中数学中的地位和意义探讨,展开相应的教学研究与案例分析。
关键词:初中数学;数形结合;教研;案例分析
引言
数学作为一门重要的研究数量关系与空间图形的理性学科,对于中学生逻辑思维、推理能力、空间意识、运算分析能力的培养具有不可替代的作用[1]。而运用数形结合思想展开教学,有助于使抽象的问题具象化,让学生能够通过图形展示,去分析代数及几何问题,使其具有更清晰的学习思路。
一、简析数形结合思想在初中数学中的地位和意义
1、地位
所谓数形结合思想,便是通过数、形之间的相互转化,让学生认识到两者之间的联系,并使知识理解更加的简单。简而言之,在初中数学教学中,形是对数的综合展示;数是形的说明。培养学生良好的数形结合思想,有助于提高课堂教学效率,促进代数与几何教学的融合,提高学生的观察、分析及思考能力,使其具有转化思想,能够从“形”中梳理出“数”的逻辑所在。因此,可以说数形结合思想是初中数学教学中较为关键的内容,既有助于锻炼学生的思维能力;又将起到促进其数学素养发展的作用。
2、意义
(1)有助于促进学生的理解,提高其思维的敏捷性
数形结合思想是较为基础的数学思维,其在数学教学中的应用十分广泛。初中数学中概念性知识较多,很多内容单依靠学生的机械记忆,并不能取得良好的教学效果。而通过数形讲解,则能够使学生快速的捕捉重点,并加强其记忆,使其思维更加的灵敏。例如:在“正数和负数”的学习中,教师可引入关于生活中汽车的南北行驶问题,其出发点为原点,也可以比作图形中的“0”,以图形中两个方向的行驶演示,使学生理解正负数概念,并体会对于有理数的应用。
(2)有助于激发学生的数学兴趣,使教学更加生动
相较于以往的一言堂数学教学,数形结合思想则是运用图形对问题的说明、展示,加强学生的理解,使数学学习更加生动、直观。例如:在“直线、射线、线段”的教学中,教师可通过图形辨识,进行授课,以帮助学生掌握初步的几何知识。
(3)有助于促进学生全方位、多角度的分析问题
在数学学习中,面对同一题目,因思路不同,其可能会产生不同的解题思路。以数形结合展开教学,有助于激发学生的想象力,引发其自主思考、多角度探究,从而使其更加全面的看待问题。
二、数形结合思想教学研究与案例分析
新课程理念的核心,便是“一切為了学生的全面发展[2]”。为提升教学的有效性,将数形结合思想渗透到中学数学中,能够使知识讲解个增加生动化、直观化。为此,笔者分别从代数和几何的教学实例中,展开相应的数、形之间转化探究:
1、在不等式中的应用
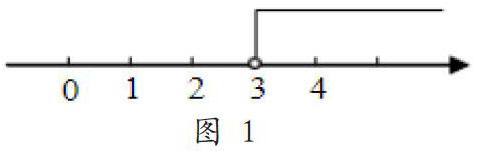
为了提升教学效率,在不等式授课中,教师可选择以数形结合的方式展开授课,以便于学生的理解与掌握。例如:在新课导入中,教师可以画数轴的方式,与学生进行教学互动。使其标注出教师给出的不同已知条件(1)小于3的正整数;(2)不大于3的正整数;(3)绝对值小于3大于1的整数等。从而引出教学。从(2)中可得出大于3的每一个数都能作为不等式x+2>5的解,不大于3的每一个数都不是它的解(具体如图1)。
2、在函数中的应用
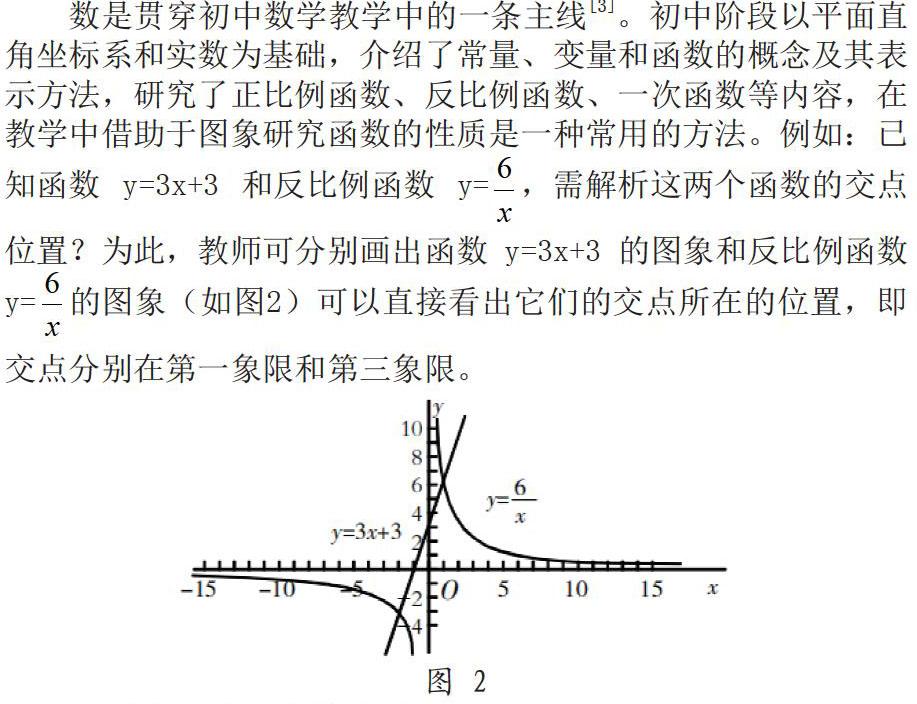
数是贯穿初中数学教学中的一条主线[3]。初中阶段以平面直角坐标系和实数为基础,介绍了常量、变量和函数的概念及其表示方法,研究了正比例函数、反比例函数、一次函数等内容,在教学中借助于图象研究函数的性质是一种常用的方法。例如:已
知函数 y=3x+3 和反比例函数 y=,需解析这两个函数的交点
位置?为此,教师可分别画出函数 y=3x+3 的图象和反比例函数
y=的图象(如图2)可以直接看出它们的交点所在的位置,即交点分别在第一象限和第三象限。
3、在勾股定理中的应用
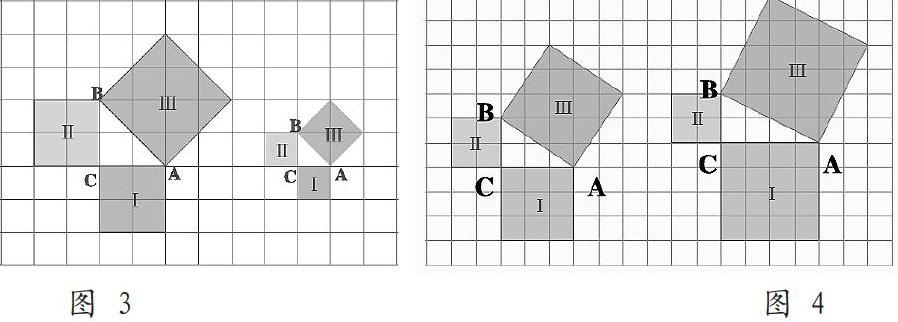
勾股定理使初中数学较为重要的一部分内容。具体教学中,教师可运用数形结合思想巩固学生对于重、难点的掌握,使其能够进行规律总结。例如:教师可出示任意直角三角形,让学生进行测量。并可进行相应的探究教学,通过画图(如图3),以直观展示,让学生们思考(1)正方形Ⅰ、Ⅱ、Ⅲ面积之间的关系;(2)等腰直角三角形三边长的关系。并以相应的直角三角形方块画格法进行教学(如图4),让其思考(1)正方形Ⅰ、Ⅱ、Ⅲ面积之间的关系;(2)直角三角形三边长的关系。给予学生充分的自主、探究、合作学习机会,并对其进行相应的思路引导,使其更好的理解几何定理。
三、结语
综上所述,构建高效课堂,培养中学生良好的数形结合思想,并非一蹴而就的。作为初中数学教师,一方面,应不断提高自身的专业能力,具有创新授课的意识,从而为学生呈现生动讲授,使其能够找到良好的数学学习技巧及方法;另一方面应注重对学生数形思想的培养,以促进其创新精神和思维能力的不断发展,为其高阶段的学习夯实基础。以此,在有效教学中,培养学生的数学核心素养。
参考文献
[1]李雪.初中数学数形结合思想教学研究与案例分析[D].河北师范大学,2014(5):20.
[2]朱家宏.初中数学教学中数形结合思想的应用[J].科技视界,2015(9):175.
[3]孟成书.初中数学数形结合教学策略分析[J].未来英才,2017(19):97.

