数理经济中可数状态下的私核与竞争均衡
黄泽曦, 李克典
(闽南师范大学数学与统计学院,福建漳州363000)
1 背景介绍
Arrow 和Debreu 在文献[1]提出数理经济中均衡模型的竞争均衡概念,并证明了在完备信息下竞争均衡的存在性,随后Aumann 在文献[2]提出了核的概念,并证明了在该经济体中核与竞争均衡是等价的,称为核等价定理.Radner 在文献[3]将竞争均衡等概念推广到有限多种状态的不对称信息经济体中.Yannelis在文献[4]中最早提出了私核的概念,Einy E 等在文献[5]中证明了配置为自由处置可行的、商人空间为无原子测度空间、状态空间为有限空间的情况下私核与竞争均衡等价,Angeloni 等在文献[6]中证明了E.Einy et al.等人的结果在配置为可行的、商人空间为无原子测度空间、状态空间为有限空间的情况下仍然成立,并在该经济模型中讨论了私弱核与私核、竞争均衡间的关系.本文将Angeloni L 在文献[6]中的部分结果推广到配置为可行的、商人空间为无原子测度空间、自然状态空间为可数空间的情况,推广了Angeloni L等关于状态空间为有限空间的部分结果.
2 经济模型
在本节将数理经济中具有不对称信息经济体的模型记为E.用无原子测度空间(T,∑,μ)代表商人空间,其中T 代表商人的集合,用 t∈T 代表商人,∑是由T 的子集生成的 σ 代数,这里∑代表商人所形成的联盟, μ 是∑上的无原子测度,用 t 代表商人.这里有可数多种的自然状态,记为 Ω={ωi}t∈N,用 Ω的划分∏t表示每个商人 t 的信息, 用F 表示由∏t生成的代数.经济体分为两期, 即=0,1.在=0时期,自然状态存在不确定性;在=1 时期,商人根据已实现的自然状态进行消费.在每种状态下,每个商人 t∈T 的消费集用表示.
对于每个商人 t∈T,用 ut代表商人的效用函数,其中满足对每个映射(t,x)ut(wi,x)是∑×B 可测的,其中 ωi是 Ω 中的某种状态,B 是的Borel 子集生成的 σ 代数.用qt代表每个商人 t 的先验知识.若用 ht(x)代表每个商人 t∈T 的期望效用函数,即
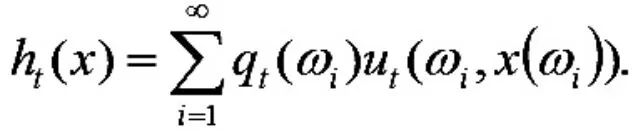
由上,可将经济体E 记为
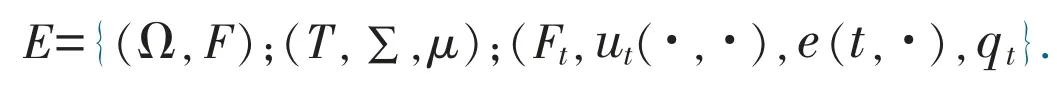
3 基本假设
本节介绍文中使用的基本假设.
1)[5]对几乎所有的 t∈T,函数 e(t,·)是 Tt可测的.
2)[5]对所有的 ωi∈Ω 和 t∈T, ut(ωi,·)是连续的、严格递增的和凹的.
3)[5]存在 K>0 使得对任意的 t∈T 和 ωi∈Ω 都有 0ut(ωi,·)K.
4)[7]存在 β >0 使得对任意的 ωi∈Ω 都有 ut(t,ωi)β1.
5)[7]存在>0 使得对任意的 ωi∈Ω 都有
4 竞争均衡与私核、私弱核
本节将私核、私弱核和竞争均衡的概念推广到可数多种状态空间,并讨论三者间的部分关系.
定义1 经济体的一个配置x 被称为可行的私人分配,若它满足
1)对几乎所有的 t∈T,函数 x(t,·)是 Ft可测的,且
2)对所有的 ωi∈Ω 都有
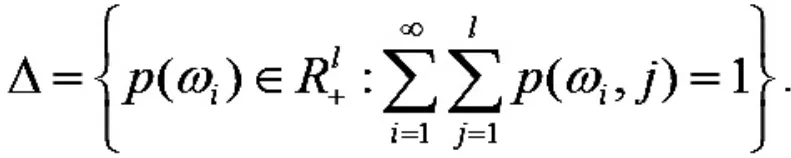
令 Mt为所有由的 Ft可测函数的集合,那么对于价格系统 p,每个商人 t 的预算集可以表示为
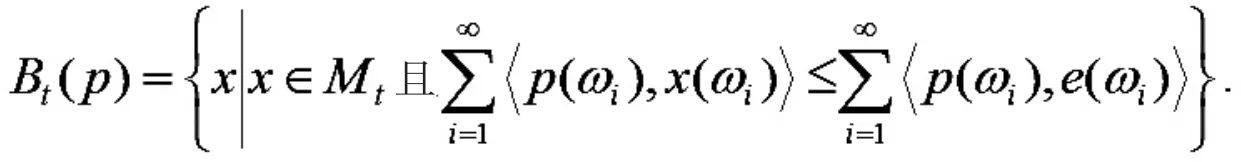
定义2 在经济体E 中配置 x 被称为私弱核分配(记为E(WC)),若它满足以下条件
1) x 是私人分配,
2) 不存在一个联盟 S∈∑和一个配置 y 使得
a) μ(S)>0,
b) 对所有的 t∈S, y(t,·)是 Ft可测的,
c) 对所有的 ωi∈Ω 都有
d) 对几乎所有的 t∈S 有 ht(y(t,·))>ht(x(t,·)).
定义3 在经济体E 中配置 x 被称为私核分配(记为E(C)),若它满足以下条件
1) x 是私人分配,
2) 不存在一个联盟 S∈∑和一个配置 y 使得
a) μ(S)>0,
b) 对所有的 t∈S, y(t,·)是 Ft可测的,
c) 对所有的 ωi∈Ω 都有
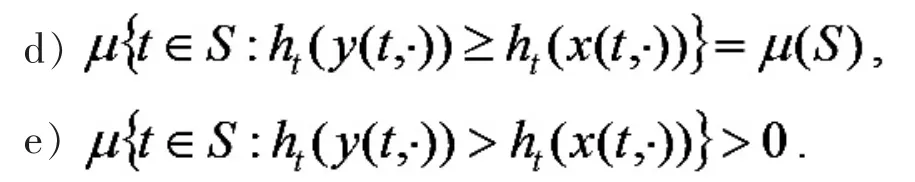
定理1 假设1)-5), 则经济体E 中每个私核分配都是私弱核分配,即E(C)E(WC).
证明由私核分配与私弱核分配的定义可得.
定义4 在经济体E 中(p,x)被称为竞争均衡(其中 p 是价格系统,x 是私人分配),若它满足以下条件.
1) 对几乎所有的 t∈T,使得 ht达到最大的函数 x(t,·)在预算集 Bt(p)中,
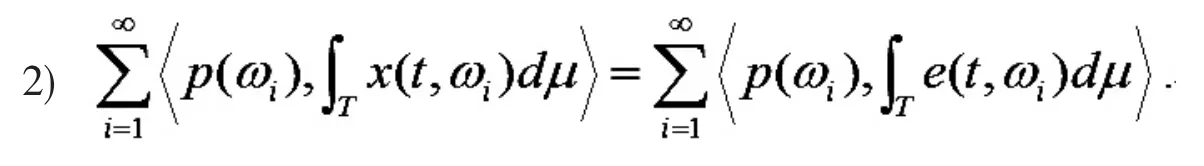
若存在一个价格系统 p 使得(p,x)是一个竞争均衡,那么称可行的私人分配 x 为竞争分配(记为E(WC)).
定理2 假设1)-5), 则经济体E 中每个竞争分配是一个私核分配,即E(W)E(C).

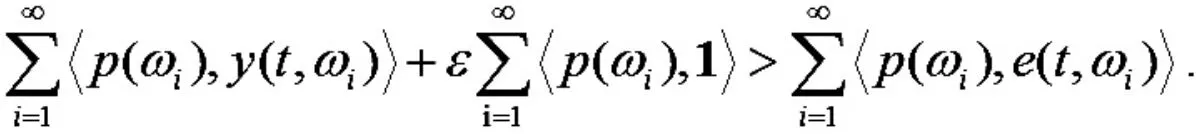
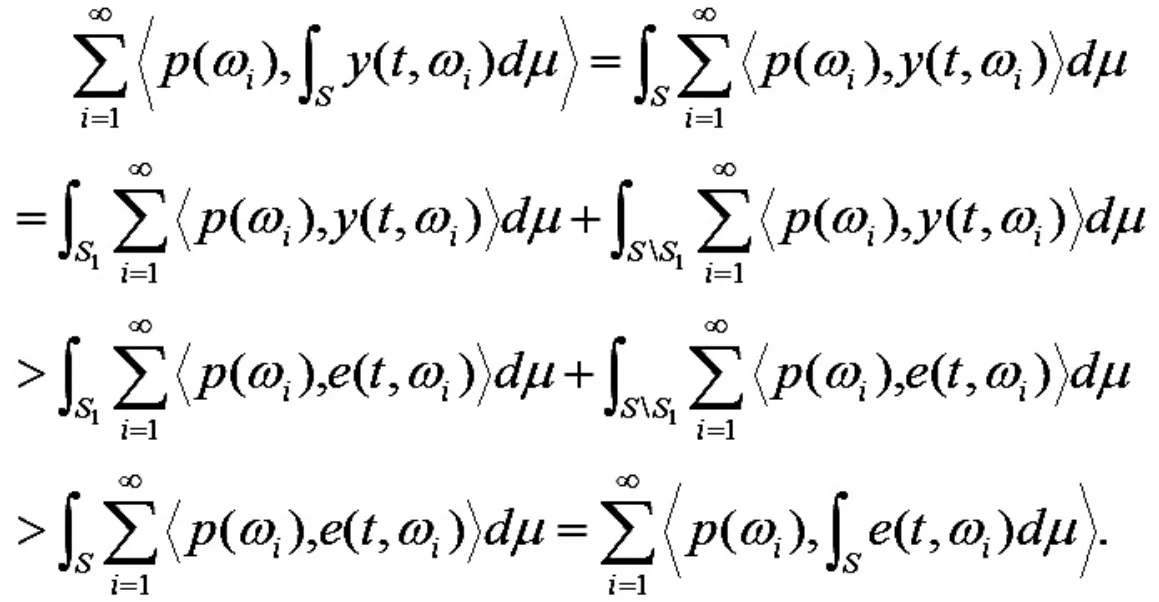
由定理1 和定理2 可得推论1.
推论1 假设1)-5),则经济体E 中竞争分配、私核分配和私弱核分配的关系为E(W)E(C)E(WC).

