基于客车乘员损伤的尖顶等效方波参数研究*

吴长风，张君媛，那景新，苏 亮，蓝平辉，卢琳兆

（1.吉林大学，汽车仿真与控制国家重点实验室，长春 130022； 2.厦门金龙联合汽车工业有限公司，厦门 361023）

前言

近年来，客车已然成为旅游、出行的主要交通工具之一［1-2］。以客车为肇事主体与其它道路车辆或障碍物发生正面碰撞的交通事件频频出现，旅客的生命安全备受社会各界的高度关注。客车的正面碰撞是一个复杂的动力学过程，国内外就客车正面碰撞方面的研究和试验法规刚刚起步［3-4］，对于其碰撞加速度波形与乘员伤害的研究也较少。因此，对客车正面碰撞开展深入研究进而减小乘员损伤风险具有重要意义。

客车发生正面碰撞时，碰撞初始动能经过车身变形吸收，并传递到后部作用于乘员区域，导致乘员向前运动与客车内饰造成二次碰撞伤害。研究表明［5-9］，客车碰撞加速度曲线与乘员的伤害具有紧密关系。但直接从客车车体中导出的碰撞加速度-时间曲线由多个不规则的峰值组成，分析较为复杂，无法用于指导乘员损伤的相关研究，此外也没有资料表明局部加速度峰值与乘员伤害的峰值有直接的关系。因此，有必要根据碰撞加速度-时间曲线的波形特点在保留应有特征参数前提下进行简化。简化后的加速度波形仍可获得与原加速度波形一致或相近的车辆位移和速度，同时，可从本质上表征碰撞响应和乘员损伤规律。

尖顶等效方波（tipped equivalent square wave，TESW）是工程实践中较为常用的波形拟合方式，具有简单、直观的特点［10-11］。同时，可以较好地表征碰撞加速度-时间曲线的特征参数。本文中以尖顶等效方波理论为基础，以客车座椅滑车系统为研究对象，采用可能出现的3种（上升型、平稳型和下降型）常用尖顶等效波形（TESW）为输入条件，对比探究波形形式对乘员损伤的影响情况，同时，在特定形式的尖顶等效方波状态下研究波形参数与乘员损伤的联系规律，并寻找有利于客车乘员保护的波形参数特点，为后续客车整车设计开发与乘员保护提供重要指导。

1 尖顶等效方波简化方法

1.1 尖顶等效方波简化

将某12 m客车以50 km／h速度做正面碰撞时乘员区第一排座椅处加速度曲线提取出来，并进行等效简化成尖顶等效波形，如图1所示。

图1 尖顶等效波形简化

尖顶等效方波与原加速度-时间曲线具有相同的碰撞变形量C和速度减为0时的时间历程tm。同时，对尖顶等效方波进行积分可以得到等效后的速度-时间曲线，如图2所示，再次积分可以得到等效后的位移-时间曲线，如图3所示。从图中可得到tm为0.107 s，C值为0.687 m。

图2 速度-时间曲线

图3 位移-时间曲线

从图2和图3可以看出，对原加速度-时间模型转化后可较好地保持原碰撞速度与位移参数特征。根据文献［12］中所述，尖顶等效方波的模型化参数可以通过下式计算获得。

式中：C为车辆碰撞最大变形量，m；v0为车辆碰撞初速度，m／s；vr为车辆反弹速度，m／s；tc为加速阶段加速度曲线与横坐标所围成图形的形心位置对应时刻，s；tm为车辆减速阶段时间或车辆反弹时刻，s；tr为车辆碰撞总时间，s；a（0）为车辆减速阶段初加速度，m／s2；a（tm）为车辆减速阶段的末加速度，m／s2；β为加速度放大因子。

1.2 尖顶等效方波可行性验证

通过以上计算公式可将客车碰撞加速度时间曲线转化成特定的尖顶等效方波。基于同一滑车座椅模型（图 4），分别加载原加速度波形和等效方波，其他边界条件保持不变，进行仿真。

图4 滑车系统模型

图5 乘员损伤结果

仿真后输出左右侧乘员头部、胸部和颈部等部位损伤结果，如图5和表1所示。从图5和表1可以看出，采用尖顶等效方波替代原碰撞加速度曲线，在工程允许的误差范围内，整个碰撞过程中乘员的动态响应和乘员的损伤曲线吻合较好，说明等效方波可替代原碰撞加速度曲线来进行客车正面碰撞的相关研究。

由 1.1节所述，尖顶等效方波主要由（0，a（0）），（tm，a（tm））和（tr，0）3个点组成，改变减速历程tm值调整a（0）与a（tm）的相对位置，客车正面碰撞过程的尖顶等效方波可分成上升型、水平型和下降型3种，如图6所示。

3种尖顶等效方波产生的碰撞能量对后部乘员区带来损伤风险存在差异，因此，有必要将3种波形作为输入，研究乘员的损伤风险，通过对比获得一种有利于客车乘员保护的方波形式。

2 尖顶等效方波-乘员损伤分析

2.1 3种TESW损伤分析

采用上述座椅滑车系统模型作为乘员损伤研究的基础模型，3种尖顶等效方波为加速度输入，其他条件不变，按照《中国客车安全评价规程》［13］（简称C-SCAP）中座椅子项目试验方法进行仿真分析，按照加权伤害准则（weighted injury criterion，WIC）［14-15］综合评价乘员头部 HIC36、胸部合成加速度Achest和左右腿最大受力Fmax3个传统部位损伤情况，具体WICt表达式为

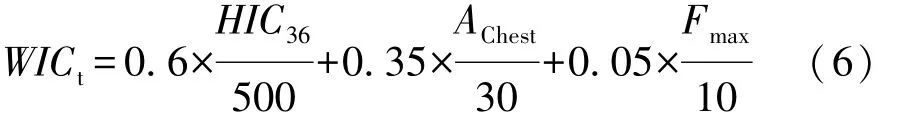
根据C-SCAP中关于座椅动态试验后乘员损伤评价，增加了乘员颈部损伤方面要求，结合Viano等［14］关于WIC乘员各部位损伤权重因子的研究，对WICt进行修正，可以得到新的WICn评价表达式，即

式中：Nij为颈部损伤准则；Fint与Mint为临界截距值，可以从相关文献［14］和文献［15］中查阅。同时，为便于数据规律总结，计算完成后仍输出右侧乘员损伤结果（表2），作为数据分析依据。

表1 乘员损伤汇总表

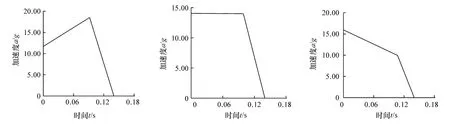
图6 3种形式的TESW

表2 3种TESW损伤结果汇总表

从表2可以发现，对于客车，下降型尖顶等效波形对后部乘员造成的综合损伤明显小于另外两种波形。因此，下降型的尖顶等效方波可以作为后续的客车设计开发的参考性波形。

2.2 下降型TESW参数与WIC的关系分析

由上节分析结果得知，下降型TESW曲线可以减小后部乘员的损伤风险。为进一步细化分析下降型TESW的参数对乘员损伤的影响，以期获得综合损伤WIC与TESW参数tm之间的关系，为后续结构设计和乘员损伤提供依据，在tm∈（0.099～0.140 s）内选取11个数值，间隔为0.004 1 s，取v0＝13.8889 m／s，C＝0.687 m和 tr＝0.140 s且保持不变。根据式（1）～式（3）可算得 TESW曲线主要参数 a（0），a（tm）和β等，得到11组数据和对应的11条下降型曲线，分别如表3和图7所示，作为滑车加速度加载输入条件。

表3 11组下降型TESW损伤结果汇总表

其中，tm＝0.140 s＝tr时刻为滑车响应总历程时间与反弹历程时间相等，碰撞出现黏滞停止状态，在该实际试验中几乎不可能出现，所以不考虑斜率最大的tm＝0.140 s的状态，可取近似时间tm＝0.139 s替代。

计算完成输出11组数据的右侧乘员损伤结果，一并列入表3中。

从表3可以看出，tm在下降型TESW取值区间内WIC并非单调变化，而是随着tm的增加先降低后升高再稍降，呈勺形变化规律，如图8所示。为便于对tm-WIC变化规律进行定量分析，结合WIC的变化趋势，对曲线进行三次多项式拟合，得到如下拟合方程。

不考虑颈部的传统WICt拟合得

图7 11组不同t m值的下降型TESW

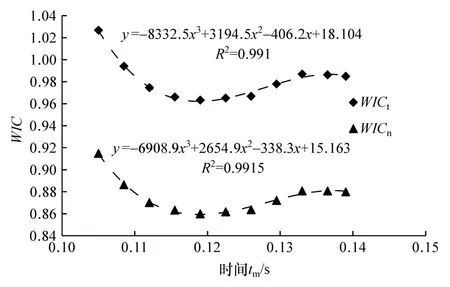
图8 t m-WIC关系图

考虑颈部的新WICn拟合得

通过对三次多项式方程求解，传统WICt曲线在tm＝0.1188 s时，有极小值 0.964；而 WICn曲线在tm＝0.1189 s时，有极小值0.859。由于两者的极小值点的时刻非常接近，几乎相同，故可认为所研究下降型TESW在 tm＝0.1189 s时有 WIC的最小值0.859。将式（2）和式（3）代入式（5）可得

其中，当 tm＝0.1189 s时 β＝0.33；客车正面碰撞速度为50 km／h时可得关系式：

通过对客车下降型TESW波形参数分析，参数C与tm的取值决定整个波形变化和影响乘员损伤情况。在客车正面碰撞正向开发研究时，可以参考上述C与tm关系，设定合理的整车变形压缩量C和减速度历程时间tm，进而减小后部乘员损伤风险。

3 结果讨论

针对目前我国客运市场典型12 m大客车结构而言，由于客车乘员区之前参与整车变形的空间较大致使减速度时间（或整车回弹时间）tm较长，结合本文研究结果，当加速度放大因子β＜1（即TESW下降波形）时，乘员损伤结果优于β≥1的其他（上升和水平型TESW）情况。同时，在β＜1的下降波形中，随着参数tm的增加，乘员综合损伤WIC呈现勺型变化特性，通过拟合曲线获得勺型特性曲线的最小值，即整车结构基于TESW波形的损伤最小值。至此，通过TESW的简化公式推导可以反向间接获得客车整车变形量C与减速度时间历程tm的关系式。进而，可以得到某款12 m客车满足后部乘员综合评价损伤WIC的结构开发流程，如图9所示。

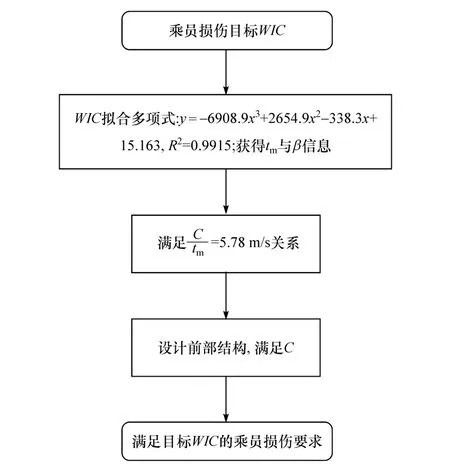
图9 某款12 m客车正面碰撞正向结构开发流程

通过上述流程，可初步设定同类型的12 m客车耐撞性的理想目标值和参考曲线，并用于指导前部结构设计，以获得满足指定WIC要求的前部结构设计与改进方案。

4 结论

运用尖顶等效方波的相关理论基础，以座椅滑车系统为研究对象，针对12 m客车可能出现常用的3种尖顶等效方波为输入条件，分析探究了方波状态和组成参数的变化对乘员损伤的影响规律。可得出以下结论：

（1）下降型TESW所造成的后部乘员损伤风险小于上升型和水平型TESW；

（2）在下降型TESW中，乘员综合损伤WIC随tm的增大，呈勺型变化；

（3）通过对WIC曲线进行三次多项式拟合，得到整车WIC最小时刻tm＝0.1189 s时，WICn＝0.859为最小值。

结合TESW模型简化推导过程可得到整车碰撞变形量参数C与减速度历程时间tm的关系式，即C＝5.78tm，该规律可为后续客车正面碰撞前部结构设计和乘员保护开发提供指导。