注重整体结构，促进有效学习

王罡

【摘要】初中数学教学中，教师仅仅依照教材内容顺序开展教学是不够的，还应注重挖掘每章内容的整体知识结构.教师需设法帮助学生探寻知识间的逻辑结构联系，以实现内容的有效过渡和衔接，同时让学生学会融会贯通.本文选取多项式乘法与因式分解和平行四边形两个典型例子在教材内容分析的基础上提出相应的教学改进策略和建议，以促进和实现学生的有效学习.

【关键词】整体性;知识结构;有效学习

美国著名教育心理学家布鲁纳曾提出认知结构学习理论，他主张“不论我们选教什么学科，务必使学生理解学科的基本结构”，同时认为知识的结构学习是通向有效学习的捷径，教师在教学中应当使用发现法引导学生学会学习.初中数学教学更是如此，一方面，初中数学各个知识点绝非单个的孤立存在，而是知识彼此间环环相扣，联系密切，故容易形成知识结构;另一方面，义务教育数学课程标准指出，“教材编写应当体现整体性，注重突出核心内容，注重内容之间的相互联系，注重体现学生学习的整体性”.鉴于此，教师理应对章节教学内容的结构了然于胸，同时在教学中帮助学生整体把握教学内容，形成知识结构图.

然而，笔者在观摩听课的过程中，不时会发现存在这样一种有待改进的不足：许多教师在课堂上往往对教学内容的全局把握能力不够，甚至平时仅注重知识点的孤立教学，只有到了章末复习小结时才会在教材的提示下帮助学生梳理本章的知识结构.显然，此时教师所做的不过是将教材内容经过理解加工转化为自己的教学内容.事实上，单元教学设计可以有效改善这一不良状况，它的整体性和综合性是一般教学设计所不能比拟的，应当成为教师日后努力的方向.只有这样，才能真正体现教师劳动的创造性，从而真正实现学生的高效学习.下面笔者选取两个典型的章节内容予以具体分析和说明.

一多项式乘法与因式分解

（一）教材内容分析

多项式乘法与因式分解是初中数学“数与代数”模块下数与式部分的重要内容，两者互为相反方向的变形.笔者分别翻阅人教版和北师版教材与之相关的章节内容，将两版本教材中的有关内容展开整体对比分析，整理成下表：

版本人教版北师版

整章知识体系整式乘法的预备知识→整式乘法→乘法公式→因式分解整式乘除的预备知识→整式乘法→乘法公式→整式除法因式分解另起一章

多项式乘法均通过转化为单项式与多项式相乘得到两个多项式相乘的运算法则;

均通过由特例到一般的归纳过程得到乘法公式

因式分解提公因式法→公式法→十字相乘法（作为课后阅读材料给出）提公因式法→公式法

图1-1 两版本教材多项式乘法与因式分解对比分析

通过整理可以看到，北师和人教两版本教材在介绍多项式乘法和因式分解时，整章知识体系及内容广度均存在一定的差异.笔者认为，相对来讲，人教版比北师版更好地呈现了该章节的知识结构，但仍有不足，例如，由多项式乘法运算法则到乘法公式的过渡和联系不够紧密等.鉴于此，教师需要适当摆脱教材内容编排体系的束缚，自主从中挖掘和开发一些新的内容，以更好地实现多项式乘法与因式分解相关内容的有效衔接.

（二）教学改进策略和建议

1.一般多项式相乘与乘法公式

根据多项式与多项式相乘的运算法则，两个多项式相乘的一般形式为（a+b）（p+q）=ap+aq+bp+bq，这主要针对两个多项式中的每一项互不相同而言.由该一般形式，教师可启发学生思考以下两个问题：

① 这里的a，b，p，q通常是两两互不相同的项，能否将该一般形式特殊化？

② 考虑某两项相同的情况，共可以分为几种特殊情况？

学生在教师的一步步提示和引导下，可以将其分为四种特殊情况：

① 某个多项式本身的两项相同，即a=b或p=q.若以a=b为例，则原形式可化简为（a+a）（p+q）=2a（p+q）=2ap+2aq，显然此时转化为单项式与多项式相乘的情形;

② 两个多项式中的某一项相同，另一项完全不同，例如，均含有a，另一项分别为p和q，原形式可化簡为（a+p）（a+q）=a2+（p+q）a+pq，此时运算结果是二次三项式.事实上，如果将a换成x，将得到x2+（p+q）x+pq型的式子，这与后续将学习的一元二次方程乃至二次函数都有着密切的联系;

③ 两个多项式中的某一项相同，另一项不同，但互为相反数（绝对值相同）.例如，均含有a，另一项分别是b和-b，此时可得到（a+b）（a-b）=a2-b2，即平方差公式;

④ 两个多项式中的两项完全相同，例如，均含有相同的项a和b，此时可得到（a+b）2=a2+2ab+b2，即完全平方公式.

与教材中以探究的形式给出几道题目并引导学生发现规律相比，显然上述做法更能突出核心内容（两个多项式相乘的运算法则），揭示一般多项式乘法与乘法公式的逻辑结构联系，有利于学生认知结构的形成.此外，初中生已经习惯了由特例到一般探寻规律的思维方式，如果教师能够按照上述改进建议让学生尝试由一般到特殊的思维方式，将有助于培养学生良好的思维品质.

2.多项式乘法与因式分解

尽管课程标准只要求学生掌握因式分解的两种方法（提公因式法和公式法），但考虑到学生后继学习及完善知识结构的实际需要，分组分解法和十字相乘法也应当成为学生了解和熟悉的内容.事实上，如果教师组织学生将前面探讨的两个多项式相乘的几种情况和因式分解的几种方法放在一起进行对比分析，学生会不禁惊讶地发现，一种情况对应一种方法，两者互为相反方向的变形.具体内容如下表：

多项式乘法的情况因式分解的方法一般形式联系该表借鉴单元教学设计的思路，试图改变根据因式分解的方法进行孤立教学的方式，将多项式乘法的情形与因式分解的方法一一对应起来，清晰地呈现了两者的联系，体现了教学内容的整体性和综合性.学生头脑中的知识结构由此形成，同时整体综合和灵活敏捷的思维品质获得了提升.

二、平行四边形

（一）教材内容分析

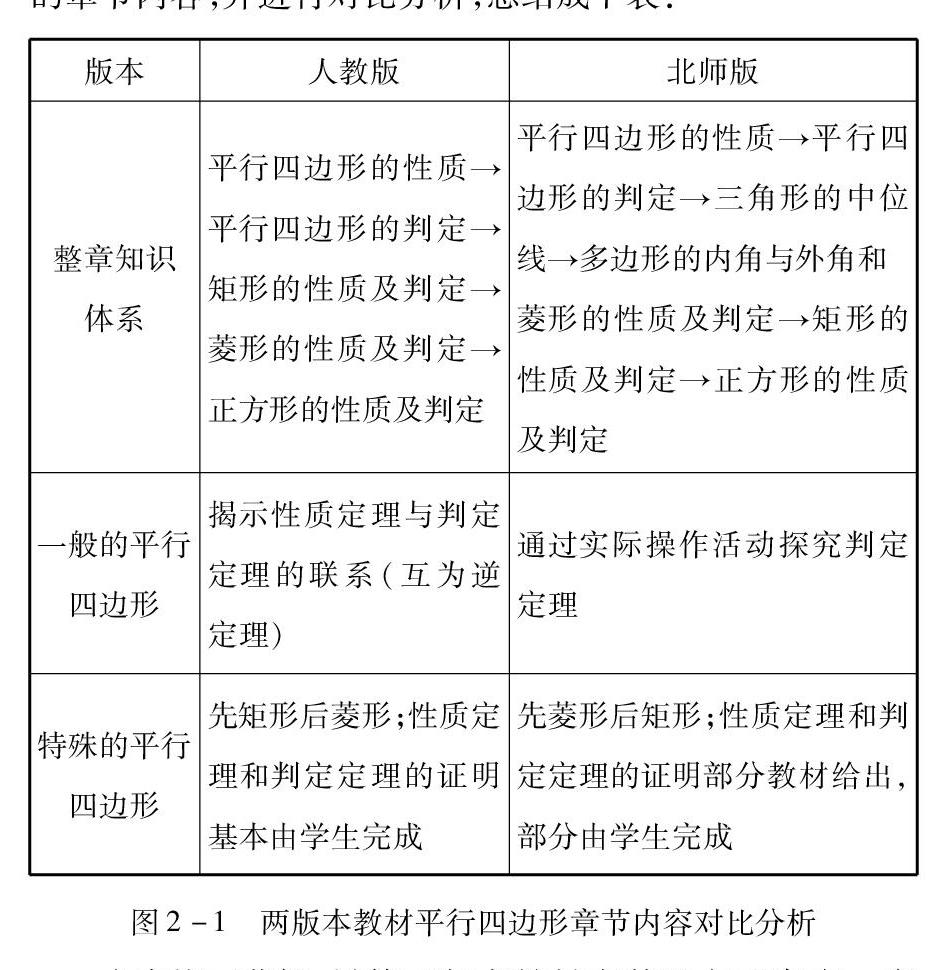
平行四边形是初中数学“图形与几何”模塊的核心内容之一，主要包括一般的平行四边形和特殊的平行四边形（矩形、菱形、正方形）.笔者翻阅人教版和北师版教材与之相关的章节内容，并进行对比分析，总结成下表：

由表格可获知，尽管两版本教材在某些方面存在一定差异，但总体内容均按照由一般平行四边形到特殊平行四边形的顺序编排.换而言之，只有当介绍完一般平行四边形的性质和判定之后，才能紧接着介绍某个特殊的平行四边形，以此类推，这样存在的一个弊端是容易将研究对象（平行四边形、矩形、菱形、正方形）人为地割裂开来，进而导致各对象间的逻辑结构联系不够密切，不利于学生形成系统的知识结构.笔者认为，为了弥补这种不足，教师在实际教学中应酌情加以改进，以丰富完善学生的知识结构.

（二）教学改进策略和建议

众所周知，三角形的两个要素分别是边和角，故可以按照内角大小将三角形分为锐角三角形、直角三角形和钝角三角形，也可以按照边长的关系将三角形分为三边不等的三角形、底和腰不等的等腰三角形以及等边三角形.同理，四边形的要素有角、边和对角线，倘若教师引导学生抓住某个要素对几类特殊的四边形（含梯形）的性质进行总结，相信学生对几类特殊四边形之间的关系将产生更深刻的理解和认识.

以“边”这个要素为例，四边形通常讨论对边和邻边，任意四边形都有两组对边和四组邻边.无论是一组对边还是一组邻边，通常需要探讨它的位置关系和数量关系，在位置关系中最特殊的便是平行和垂直，在数量关系中最特殊的便是相等.基于以上考虑，常见的特殊四边形的性质归纳如下：

三、总 结

由上述举例分析可见，尽管教材呈现出数学知识间的逻辑顺序，并在章末给出相应的知识结构图，但作为教师，如果过分依赖教材，不能在吸收教材合理因素的基础上进行再创造，将不利于对教学内容整体性的把握.事实上，教师在教学实施时，应对教材内容进行深度挖掘和加工，尽可能阐释教材没有或未能呈现的内在前后逻辑结构联系，以期帮助学生把握数学内容的本质，完善学生的知识结构，最终实现学生的有效学习.

【参考文献】

[1]涂荣豹，季素月.数学课程与教学论新编[M].南京：江苏教育出版社，2007：440-442.

[2]中华人民共和国教育部.义务教育数学课程标准[M].北京：北京师范大学出版社，2012.

[3]李铁安.义务教育课程标准案例式解读——初中数学[M].北京：教育科学出版社，2012：195-197.

[4]罗新兵，王光生.中学数学教材研究与教学设计[M].西安：陕西师范大学出版社，2011：62-65.