声测连发弹丸炸落点坐标的快速定位方法

冯 松，张亚辉，尚书贤，陆永安

(中国人民解放军63875部队， 陕西 华阴 714200)

声测定位技术是利用声学与电子装置接收声信号以确定声源位置的一种技术，具有全天候、低成本等优点[1-6]。声学炸点测量系统基于被动声测技术，捕捉弹丸爆炸时产生的声信号，采用时延估计方法由几何关系确定炸点的空间坐标。

在声学测量设备[7-10]求解连发弹丸落点过程中，对于三维落点坐标，这里指坡地的落点坐标测量，直接采用方程求解的方法，存在求解困难的问题，提出采用构建坡地三维曲面，空域搜索时空匹配算法来求解弹丸的炸落点三维坐标，在此过程中，如果采用了较大的步长，计算时间短，但精度不高；如果采用较小的步长，精度高，但耗费的时间却很长。针对此问题，提出连发弹丸声测数据落点坐标实时处理算法优化方法，即先采用大步长搜索目标区域，然后采用小步长精确定位，即保证了测量精度，也提高了数据处理速度。

1 空域搜索时空匹配算法

在声测设备得到连发弹丸波达时刻数据后，求解连发炸点坐标过程中，主要存在以下问题：

1) 坡地三维炸点实时定位算法；

2) 多弹丸声波达时刻到达顺序混乱条件下快速匹配计算问题。

对于连发弹丸目标，直接采用方程求解的方法非常困难[11]，为了解决上述问题，提出了基于空域搜索时空匹配的连发炸点定位算法，首先需要根据炸点坐标的测试区域(包含极值点)构建一个三维的曲面，该曲面能够接近实际的炸点落弹区域，然后，在曲面上进行搜索，找到与测量分站测得的波达时刻匹配的点坐标，即为该弹丸的落点坐标。该曲面搜索算法是在测量分站正确获得弹丸落地的波达时刻基础上进行的，对如何获取波到达时刻本文不再论述。

1.1 固定步长区域搜索算法

在连发坐标解算中，从每个传感器数据中任取一个波达时刻数据，合并成一个组合，所有可能的组合形成一个集合，然后根据对各站时刻组合与建立的曲面对应的时差数据库匹配，求出多个可能的炸点坐标及一致性系数，最后根据炸点空间和时间上的唯一性剔除假目标。下面以4发弹丸炸点坐标和5个测量分站为例：

步骤1 建立空域各点时差数据库

设测试分站坐标为：

Sensor_x=[x1,x2,x3,x4,x5]′

Sensor_y=[y1,y2,y3,y4,y5]′

Sensor_z=[z1,z2,z3,z4,z5]′

则对于空间任何一个爆炸时刻T，炸点坐标为W(x,y,z)的炸点而言，爆炸声波到达各个传感器的波达时刻为矩阵t为：

[t1t2t3t4t5]=T+l/c

l为爆炸点到各测量分站的距离，计算出矩阵t中的最小值tm，为了仅仅体现爆炸位置而忽略爆炸时刻，将矩阵t作如下处理，得到矩阵tt：

tt=[t1-tmt2-tmt3-tmt4-tmt5-tm]

将其进一步表示为：

tt=[tt1tt2tt3tt4tt5]

称其为对应点时差数据库矩阵。

对于可能的落弹区三维空间，可根据试验前，测得的边界范围和在该范围内存在的极值点，构成一个三维落单区曲面，然后以一定的步长d穷举，可得到空间中任何一个点对应的矩阵tt，将其存入一个数据库。

步骤2 各站波达时刻全排列组合

对各个测试站获取的波达时刻进行全排列组合，假设炸点数为n，测试站数为5，那么全排列数为：p=n5。设炸点数为4，测试站数为5，那么全排列数为：45=1 024。

步骤3 计算时空符合性系数

时空一致性符合系数表示为：

判定规则为，ttt越小，时空符合性越好。

根据各组合中的波达时刻，穷举数据库中的元素，计算出各元素对应的时空符合性系数，找出最好的那个点并计算其时空符合性系数。最后，每个组合找到一个点及其对应的时空一致性系数，总数量为45=1 024。从这里可以看出数据量的大小除了和连发弹丸的数量有关外，跟建立的时差数据库中的数据多少有直接的关系，即建立数据库时，步长越小，穷举时数据量就越多，耗费的时间也就越多，直接影响到了数据处理的实时性。

步骤4 建立时空符合性判定规则

假设一般测试最大误差为δ，c为声速，单位m，设定阈值Y

Y=5δ/c

数据库ttt值最小，且小于等于Y的点为所求炸点坐标。另外，在计算多目标炸点时，所有波达时刻值只允许被使用一次。

师：次数越高，方程越复杂.数学史上，人们很希望能像低次方程那样去求解高次方程，但经过长期的努力，问题都没有得到解决.1824年，年仅22岁的挪威天才数学家阿贝尔(N.H.Abel，1802—1829)成功地证明了五次及以上的一般方程没有根式解.那么，我们是否还有其他的途径解决方程是否有实数根的问题？

步骤5 搜索与炸点数对应的最优组合及最优坐标

对45=1 024个点进行二次寻优，找到时空一致性最好(系数最小)的那个组合及对应点作为第一个炸点；接着找第二个(系数值按小到大排列第二个)，若其对应点的波达时刻未被第一个点使用过，且其时空一致性系数小于Y，认为其为第二个炸点，同理查找剩余炸点坐标。

1.2 变步长区域搜索算法

在该算法中，步骤1、步骤2、步骤4、步骤5步骤相同，不同在于步骤3，在连发定位中，随着连发弹丸数量增多，搜索算法计算量指数增加。采用先大步长粗定位，再在粗定位区域小步长搜索的方法进行，在保证精度的情况下提高数据处理的实时性。根据算法思想，首先确定变步长算法中相关参数的准测，具体步骤如下：

1) 小步长d的确定

假设测量设备的测时精度为q(ms),其对应的理论距离误差为q×c/1 000(m)，其中c为声速，小步长d可确定在1/3×q×c/1 000(m)附近选取。假设声测设备的波达时刻估计精度优于4(ms)，其理论测量精度应优于4×331/1 000≈1.3 m，根据小步长确定原则，得到d=1.3/3≈0.4 m，所以小步长可取d1=0.5 m，d2=0.4 m，d3=0.3 m，最终确定在满足精度要求下选择d为0.5 m，相比其他值具有较小的运算量。

2) 大步长L的确定

在理论上大步长应取小步长的整数倍，并且满足：

ymin=M×N/L2+k*L2/d2

式中y表示参与计算的数据个数，M,N为落弹区域距离和方向的长度，L为大步长，d这里取0.5，k为连发数量。求得上式中的最小值所对应的L即为理论上最优大步长，最终结果以实际仿真数据为准。

3) 搜索范围的确定

假设测量范围1 500 m(横向)×1 000 m(纵向)落弹区域(高程范围0～200 m)，4连发弹丸射击，弹丸落地爆炸间隔时间设为0.2 s。声测设备采用5个测量站进行测量。仿真参数如下(单位m)：

a) 传感器坐标

Sensor_x=[0 0 1 000 1 500 1 500]′

Sensor_y=[0 1 500 0 100 500]′

Sensor_z=[0 0 0 180 182]′

b) 搜索边界和局部极值点(共12个点)

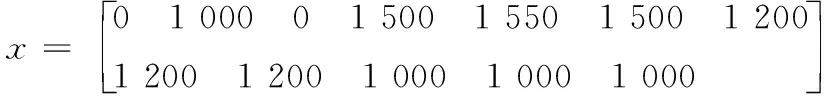
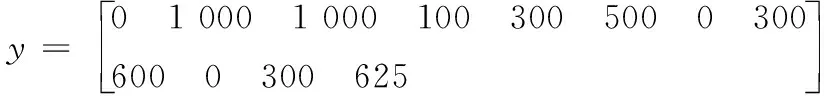
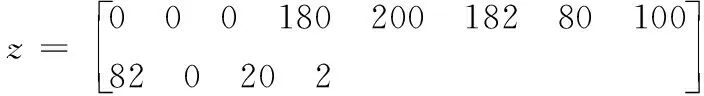
c) 4连发炸点坐标真值

xd=[1 200 1 183 1 195 1 200]

yd=[320 207 297 201]

zd=[98 85.3 98.1 93.3]

根据以上条件，采用较大的步长L(这里随机取值25 m)，通过搜索算法，先初定位，确定第一个炸落点坐标P(x1,y1,z1)。如图1所示，得到模拟炸点P(1 200,325,98.5)。

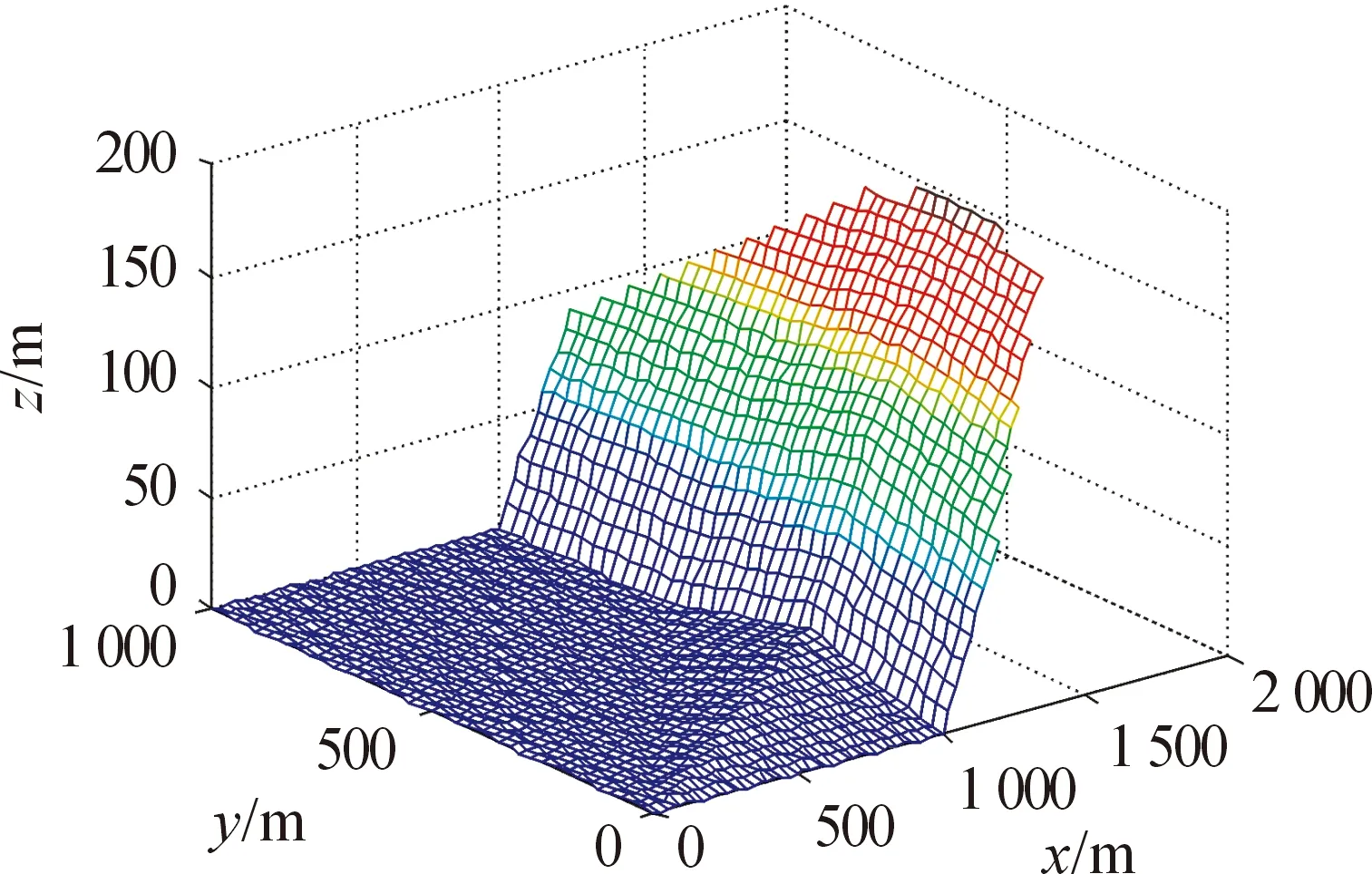
图1 大步长构建的空间区域

以该P点为中心，包含A(x1-L,y1-L,zA)、B(x1-L,y1+L,zB)、C(x1+L,y1-L,zC)、D(x1+L,y1+L,zD)，5个点构成一个新的搜索区域Q2，x∈[1 175 1 225],y∈[300 350],z∈[81.6 102.7],如图2所示。

在Q2上采用小步长d(这里取值0.5)进行细分，建立对应的数据库，再次通过搜索算法得到一个精确的炸落点坐标(1 200，320，97.9)，如图3所示。

其余的炸落点坐标计算方法相同。

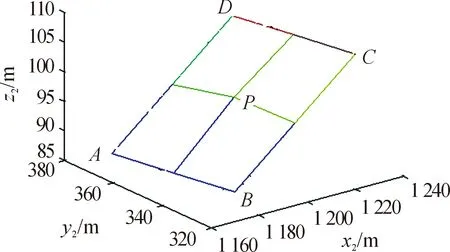
图2 搜索区域Q2上PABCD点

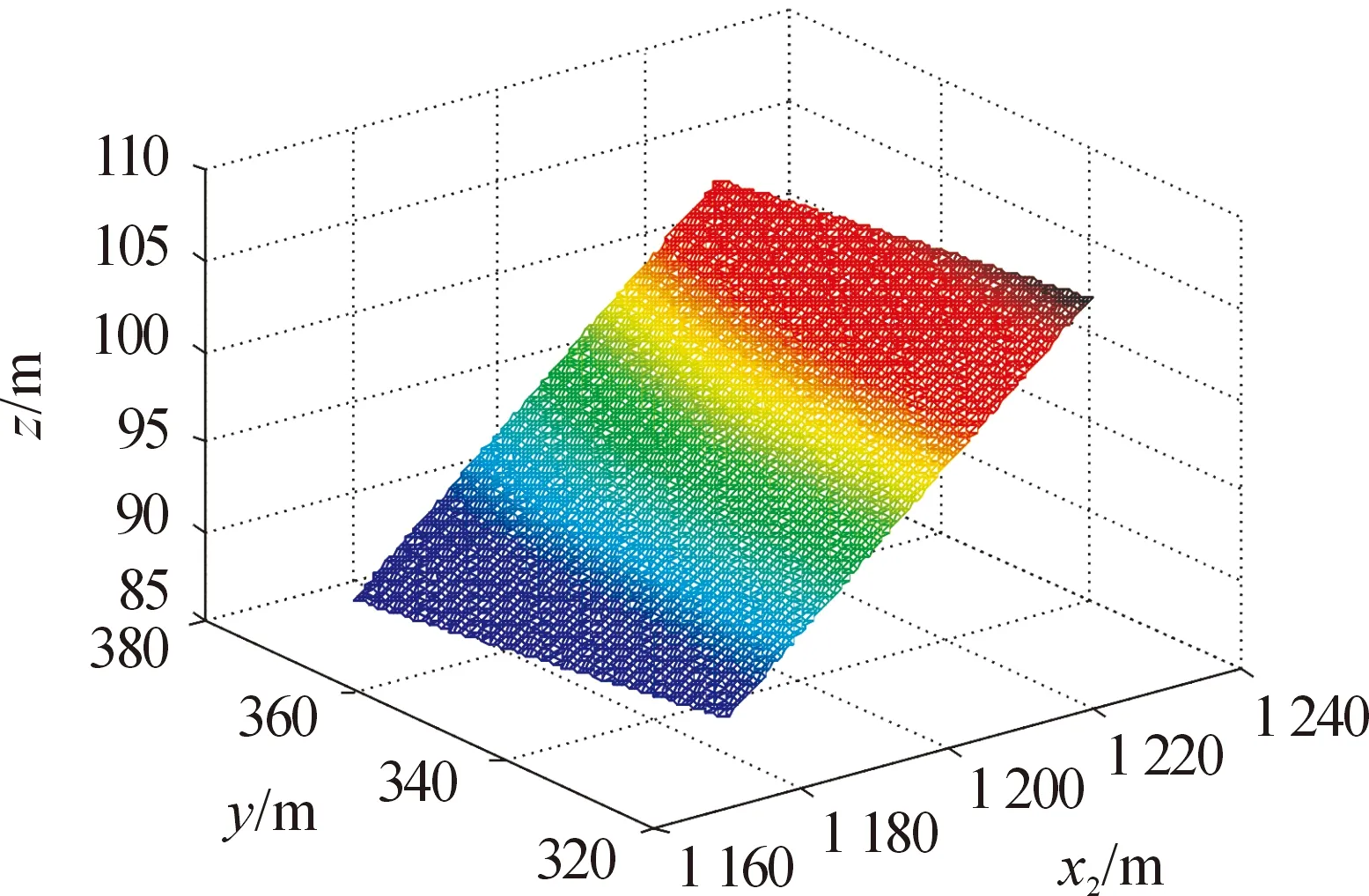
图3 搜索区域Q2进行细分示意图

2 仿真分析

同样根据以上设定条件，采用固定步长和变步长两种方法进行仿真，结果如下。

2.1 运算时间

从表1得到，在固定步长情况下，步长越小，运算的时间就越长。在小步长d=0.5时，大步长L需要是其整数倍，通过计算公式和仿真可得到如下结果：

ymin=M×N/L2+k*L2/d2

已知M=1 500，N=1 000，d=0.5，k=4，可以求得在L=17，y得到最小值，即为理论上的最优大步长。下面进行实际运算仿真，结果如表2所示。

表1 定步长运算时间结果

表2 在d=0.5,改变大步长运算时间

从表2可以看出，理论上L取值17最优，但实际上，L取值13运算时间最短，这是因为在进行二次搜索过程中，其时间运算量与首次搜索的时间运算量不是成正比的关系。

综上可得，变步长的运算时间明显优于固定步长解算时间，在变步长参数选取时，采用L=13 m，d=0.5 m，具有较快的运算速度。在实际测量弹丸炸落点坐标过程中，可以事先根据已知条件进行仿真，达到最优的大步长L值。

2.2 数据量

根据仿真条件，选用固定步长(d=2 m)时，在该区域中，采用定步长分割，有376 251个数据点，对应具有376 251个时差数据库，然后进行匹配，数据量较大，耗费的时间较长。

在变步长搜索算法中，L=13 m，d=0.5 m，有11 981个数据点，对应具有11 981时差数据库，是固定步长搜索算法数据量的3.2%，所以，数据计算量大幅度减少。

2.3 数据精度

根据初始仿真条件，设定获取的波达时刻误差为零，且不考虑风速的影响，4连发弹丸落点坐标采用固定步长(d=2 m)进行曲面搜索，得到4个炸点坐标，其中两个比较接近，结果如图4所示。

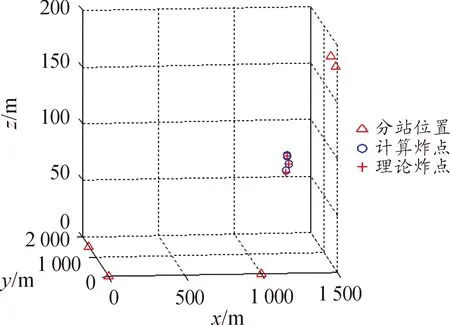
图4 固定步长d=2 m计算结果

同样的仿真条件下，4连发弹丸落点坐标采用变步长(L=13，d=0.5 m)进行曲面搜索，得到4个炸点坐标，其中两个比较接近，结果如图5所示。

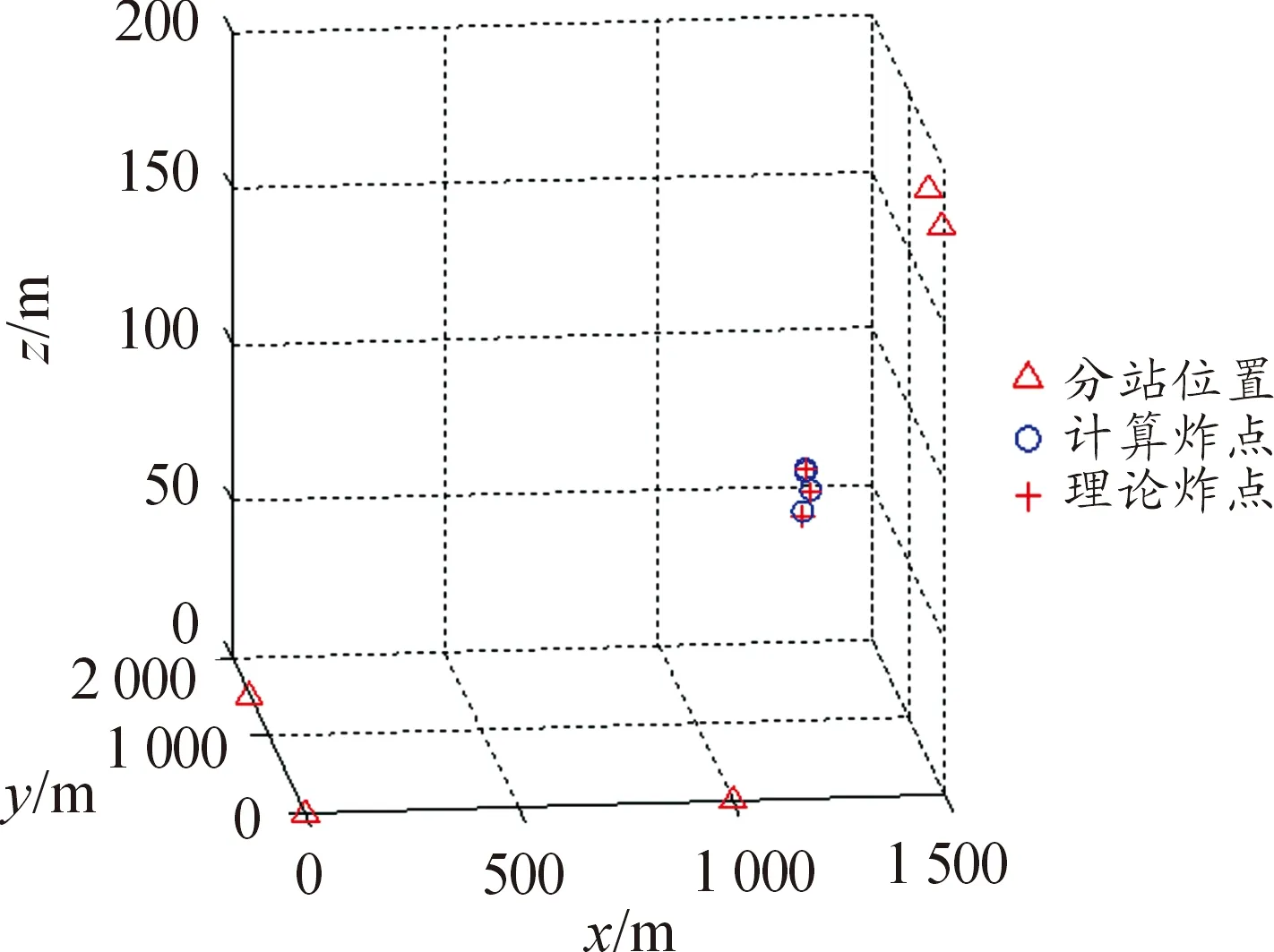
图5 变步长L=13,d=0.5计算结果

根据仿真条件，分别采用固定步长和变步长算法得到4连发弹丸坐标如表3所示。

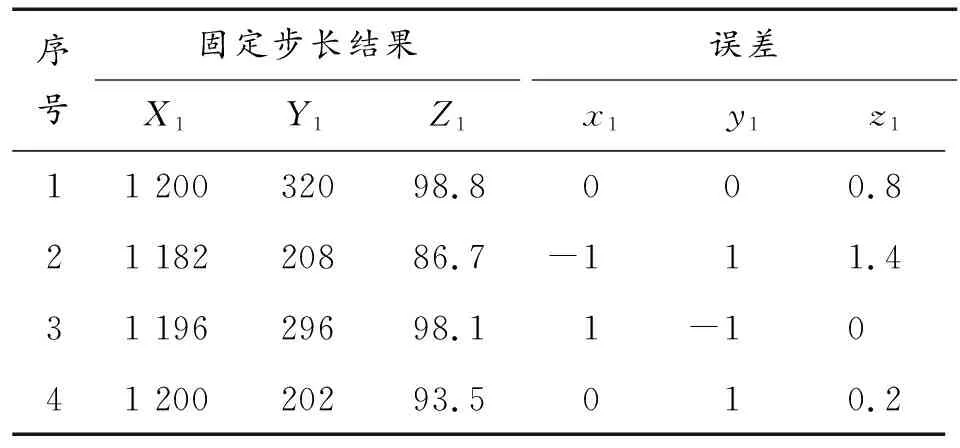
表3 4连发计算结果数据对比

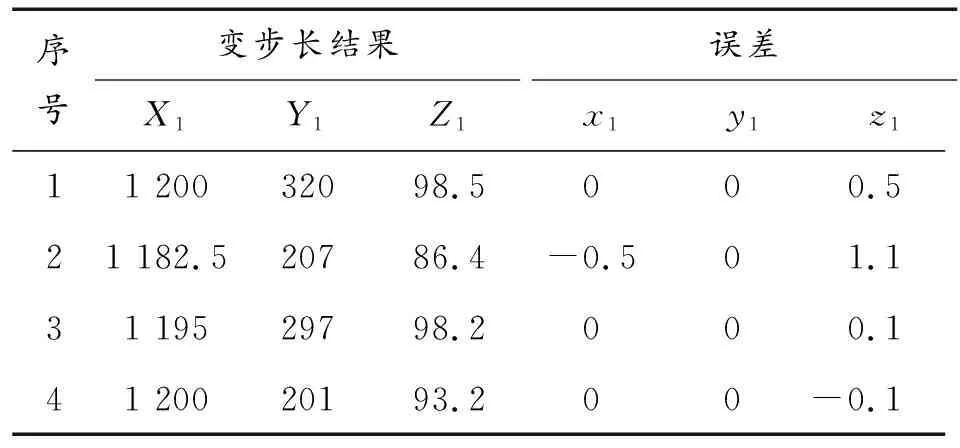
续表(表3)

从以上3项结果可以看出，采用变步长的空间区域搜索算法，能够在保持精度和提高精度的情况下，减少数据运算量，对以后多连发数据实时处理提供了依据。

3 结论

在声学测量基础上，提出基于空域搜索时空匹配算法思想，提供了一种变步长炸落点坐标数据优化算法，能够在同精度的情况下(搜索精度0.5m)，4连发炸点坐标数据处理时间由278.4s提高到1s，提高了数据处理速度,有效提高连发炸落点坐标数据处理的实时性，为以后多连发、多齐射弹丸数据处理提供了一种思路，具有较好的应用前景。