基于互协方差的L型嵌套阵列二维波达方向估计

高晓峰， 栗苹， 李国林， 郝新红， 贾瑞丽

(北京理工大学 机电动态控制重点实验室， 北京 100081)

0 引言

波达方向(DOA)估计作为阵列信号处理技术中的重要领域，在无线通信、水下探测[1-2]、声探测[3-4]、雷达探测[5]等领域具有广泛应用。近年来，不同阵列结构的二维DOA估计研究越来越受到关注，如双平行阵[6-7]、圆阵[8-9]、十字阵[10-11]、矩形阵[12-13]、L型阵[14-19]等。与其他阵列相比，L型阵因其具有更好的估计性能和更低的克拉美罗界[20]成为二维DOA估计的研究热点。文献[14]提出将传播算子方法应用到L型阵列上进行二维DOA估计,避免了对协方差矩阵进行奇异值分解和特征值分解。文献[15]提出利用L型阵列互相关矩阵的二维DOA估计方法，利用互相关矩阵消除了噪声影响。文献[16]提出一种基于L型阵列的互相关矩阵联合奇异值分解的DOA估计方法，利用互相关矩阵实现角度自动匹配。文献[17]提出一种基于L型阵列的二维盲DOA估计方法，将不同方向的阵列分解出满足子空间旋转不变性的子阵，在不同方向分别利用旋转不变子空间技术(ESPRIT)算法进行DOA估计。文献[18]提出利用L型阵列不同方向的阵元信号进行互协方差运算，利用互协方差矩阵构建两个互为共轭的矩阵，对矩阵进行奇异值分解，实现二维DOA估计。文献[19]提出一种基于L型阵列的低复杂度二维DOA估计方法，将互相关矩阵划分为不同子矩阵，利用满足旋转不变性的传播算子方法进行二维DOA估计。上述基于L型阵列的DOA估计算法大多为针对均匀阵列的子空间类算法，需要对协方差矩阵采用特征值或奇异值分解等信号处理方法划分信号子空间和噪声子空间，估计性能受信噪比的影响较大，在低信噪比环境下算法估计精度较差。均匀阵列的角度分辨率与阵元孔径呈反比，可估计的空间信源数小于阵元数，因此在阵元数有限时均匀阵列受限于阵列孔径和阵元个数，难以获得较高的DOA估计精度，可估计的空间信源数较少。

与均匀阵相比，稀疏阵在阵元数相同情况下具有更大的孔径、更小的阵元间互耦效应，因此获得了学术界的广泛关注，如最小冗余阵列[21]、互质阵列[22]和嵌套阵列[23]等。与其他稀疏阵相比，嵌套阵列易于构造，产生的虚拟阵列具有固定的解析表达式，利用接收信号的协方差矩阵由O(M)个阵元(M为阵元数)能够获得O(M2)的自由度，具有较好的DOA估计效果。

本文针对上述L型均匀阵列在二维DOA估计中的问题，提出一种基于互协方差的L型嵌套阵列二维DOA估计算法。采用由两个相互正交的2阶嵌套阵构成的L型阵列，利用不同子阵信号进行互协方差运算，得到互协方差矩阵，并基于不同子阵噪声不相关、互协方差矩阵消除了噪声的影响；对互协方差矩阵进行列向量化、产生无冗余阵元的虚拟阵列，利用虚拟阵列及其共轭矩阵构建满秩的Toeplitz矩阵作为等效协方差矩阵；利用等效协方差矩阵之间的子空间旋转不变性，通过ESPRIT算法实现了目标的方位估计；基于虚拟阵列等效信源向量的唯一性，通过估计虚拟阵列的等效信源向量实现空间信源的角度匹配。与L型均匀阵列相比，本文算法通过互协方差矩阵产生了更多的虚拟阵元，获得了更高的角度自由度，在低信噪比环境下具有更高的估计性能，但也不可避免地增加了计算复杂度，在实际应用中针对具体应用背景需要加以考虑。

符号说明：(·)T、(·)H、(·)-1分别表示矩阵转置、共轭转置、求逆；diag(·)表示对角矩阵；∏N表示N×N阶的反对角单位矩阵；⊙表示Khatri-Rao积；vec(·)表示矩阵列向量化；λ表示来波波长。

1 阵列接收信号模型

阵列模型如图1所示：L型嵌套阵由两个相互正交的2阶嵌套阵构成，x轴天线阵列和y轴天线阵列均由阵元数为N-1、阵元间隔为d=λ/2的均匀线阵，以及阵元数为N、阵元间隔为Nd的均匀线阵构成；x轴天线阵列的阵元位置为p=[ξd,0,0]，y轴天线阵列的阵元位置为q=[0,ξd,0]，ξ={0,1,…,N-2,N-1,…,N2-1}，原点处公共阵元为参考阵元。

图1 L型嵌套阵列结构图Fig.1 Array configuration of L-shaped nested array

图1中：si(t)表示第i个入射信号，i=1，…，k，k为独立远场窄带信号的个数；θ=[θ1,θ2,…,θk]表示入射信号的俯仰角；φ=[φ1,φ2,…,φk]表示入射信号的方位角；α=[α1,α2,…,αk]表示入射信号与x轴之间的夹角；β=[β1,β2,…,βk]表示入射信号与y轴之间的夹角。设空间存在的k个独立远场窄带信号入射到阵列上，阵列输出噪声为0均值、σ2方差的高斯白噪声。为了方便计算，在如下公式中用(α,β)代替(θ,φ)，角度转换关系如(1)式所示：

cosα=cosθsinφ，
cosβ=sinθsinφ.

(1)

x轴天线阵列接收到的信号向量可以表示为

X(t)=[x1(t),x2(t),…,x2N-1(t)]T=
Ax(α)S(t)+Nx(t)，

(2)

式中：Ax(α)=[ax(α1),ax(α2),…,αx(αi)，…,ax(αk)]为x轴阵列的方向矩阵，其中

ax(αi)=[1,…,e-jπ(N-1)cos αi,…,e-jπ(N2-1)cos αi]T；

(3)

S(t)=[s1(t),s2(t),…,sk(t)]T为入射信号源向量；Nx(t)为x轴阵列接收到的高斯白噪声向量。

y轴天线阵列接收到的信号向量可以表示为

Y(t)=[y1(t),y2(t),…,y2N-1(t)]T=
Ay(β)S(t)+Ny(t)，

(4)

式中：Ay(β)=[ay(β1),ay(β2),…,ay(βi)，…,ay(βk)]为y轴阵列的方向矩阵，其中

ay(βi)=[1,…,e-jπ(N-1)cos βi,…,e-jπ(N2-1)cos βi]T；

(5)

Ny(t)为y轴阵列接收到的高斯白噪声向量。

2 基于L型嵌套阵的二维DOA估计算法

2.1 基于互协方差的虚拟阵列生成

2.1.1x轴虚拟阵列生成

x轴阵列划分为两个子阵,子阵1为x轴阵列前N个阵元组成的阵元间隔为λ/2的均匀线阵，其接收信号为

X1(t)=[x1(t),x2(t),…,xN(t)]T=
Ax1(α)S(t)+Nx1(t)，

(6)

式中：Nx1(t)为子阵1接收到的噪声向量；Ax1(α)=[ax1(α1),ax1(α2),…,ax1(αi)，…，ax1(αk)]为子阵1的方向矩阵，其中

ax1(αi)=[1,e-jπcos αi，…,e-jπ(N-1)cos αi]T.

(7)

子阵2为x轴上第N个阵元到第2N-1个阵元组成的阵元间隔为Nλ/2的均匀线阵，其接收信号为

X2(t)=[xN(t),xN+1(t),…,x2N-1(t)]T=
Ax2(α)S(t)+Nx2(t)，

(8)

式中：Nx2(t)为子阵2接收到的噪声向量；Ax2(α)=[ax2(α1),ax2(α2),…,ax2(αi),…,ax2(αk)]为子阵2的方向矩阵，其中

ax2(αi)=
[e-j(N-1)πcos αi,e-j(2N-1)πcos αi,…,e-j(N2-1)πcos αi]T.

(9)

子阵1的接收信号逆向排序，

X1z(t)=∏NX1(t)=
[xN(t),xN-1(t),…,x1(t)]T=
Ax1z(α)S(t)+Nx1z(t)，

(10)

式中：Ax1z(α)=[ax1z(α1),ax1z(α2),…,ax1z(αi),…,ax1z(αk)]，ax1z(αi)=[e-jπ(N-1)cos αi，e-jπ(N-2)cos αi,…,1]T。

逆向排序后的子阵1接收信号和子阵2接收信号进行互协方差运算，得到互协方差矩阵Rcx：

(11)

互协方差矩阵Rcx向量化，按列拉伸成1个N2×1阶的长向量，表达式如下：

(12)

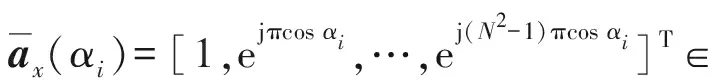
(13)

2.1.2y轴虚拟阵列生成

y轴上的阵元划分为两个子阵,子阵3为y轴上前N个阵元组成的阵元间隔为λ/2的均匀线阵，子阵4为y轴上第N个阵元到第2N-1个阵元组成的阵元间隔为Nλ/2的均匀线阵，其接收信号为

Y1(t)=[y1(t),y2(t),…,yN(t)]T=
Ay1(β)S(t)+Ny1(t)，

(14)

Y2(t)=[yN(t),yN+1(t),…,y2N-1(t)]T=
Ay2(β)S(t)+Ny2(t)，

(15)

式中：Ny1(t)、Ny2(t)分别为子阵3和子阵4接收到的噪声向量；Ay1(β)=[ay1(β1),ay1(β2),…,ay1(βi),…,ay1(βk)]为子阵3的方向矩阵，

ay1(βi)=[1,e-jπcos βi，…,e-j(N-1)πcos βi]T；

(16)

接收信号Ay2(β)=[ay2(β1),ay2(β2),…,ay2(βi),…,ay2(βk)]为子阵4的方向矩阵，

ay2(βi)=
[e-j(N-1)πcos βi,e-j(2N-1)πcos βi,…,e-j(N2-1)πcos βi]T.

(17)

子阵3的接收信号逆向排序得到Y1z(t)，将Y1z(t)与子阵4的接收信号Y2(t)进行互协方差运算，得到互协方差矩阵Rcy. 由于不同子阵噪声不相关，互协方差矩阵中的噪声项被消除。

(18)

式中：Ay1z(β)=[ay1z(β1),ay1z(β2),…,ay1z(βi),…,ay1z(βk)]，ay1z(βi)=[e-j(N-1)πcos βi,e-j(N-2)πcos βi,…,1]T.

互协方差矩阵Rcy向量化，按列拉伸成1个N2×1阶的长向量，表达式如下：

(19)

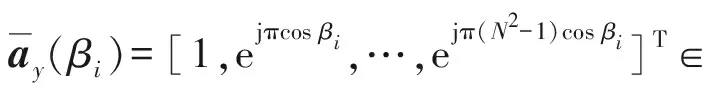
(20)

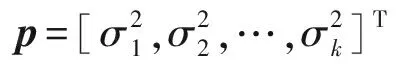
2.2 基于共轭矩阵的协方差矩阵构造

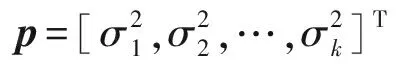
定义x轴的虚拟阵列接收信号为

(21)

(22)

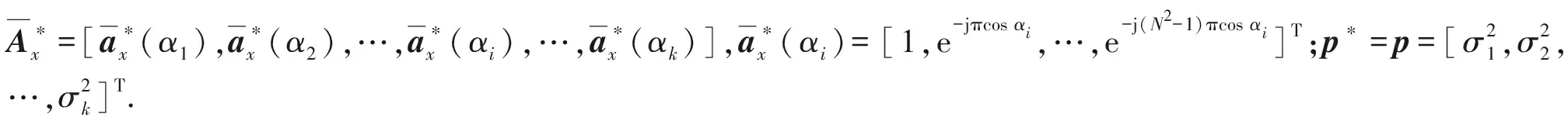
(23)

(24)

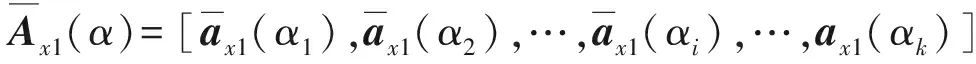
针对X1和X2，利用ESPRIT算法求解角度α，构造如下矩阵：

(25)

对矩阵Cx进行奇异值分解，得到k个大特征值对应的特征向量构成的矩阵Ex：

(26)

式中：T为k×k阶的满秩矩阵。利用虚拟阵列信号的旋转不变性可得Ωx(α)：

(27)

由(27)式可知，对Ωx(α)进行特征值分解可得特征值u，即可得到角度，

=arccos(arg(u)/π).

(28)

同理，定义y轴的虚拟阵列接收信号为ry:

(29)

(30)

(31)

同理，针对Y1和Y2，利用ESPRIT算法求解角度β，构造如下矩阵：

(32)

由(26)式、(27)式，同理对矩阵Cy进行奇异值分解，可以求得Ωy(β)，对Ωy(β)进行特征值分解可得特征值v，即可得到角度：

=arccos(arg(v)/π).

(33)

2.3 角度匹配

由(28)式、(33)式可知，本文所提算法的两个角度估计值和是通过两次一维DOA估计得到的，角度和担的估计值是失配的。本文提出利用虚拟阵列等效信源向量的唯一性进行角度匹配。采用(28)式得到的角度重构x轴方向虚拟阵列的方向矩阵由(12)式可知信源向量p可由阵列方向矩阵和虚拟阵列信号rx估计得到。通过最小二乘法可得信源向量的估计值1：

(34)

(35)

(36)

(37)

(38)

=Ц.

(39)

本文所提算法具体计算步骤如下：

1)x轴和y轴上的阵元分别划分为两个子阵，其接收信号分别为X1、X2和Y1、Y2，将X1和Y1逆向排序得到X1z、Y1z，将X1z和X2进行互相关运算得到Rcx，将Y1z和Y2进行互相关运算得到Rcy；

2) 由(12)式、(19)式，利用互协方差矩阵Rcx和Rcy向量化产生虚拟阵列信号rx和ry，等效信号源为全相干实包络信号；

3) 利用虚拟阵列信号及其共轭矩阵构造满秩的Toeplitz矩阵，作为等效协方差矩阵实现解相干，基于ESPRIT算法得到目标角度的估计值和；

2.4 算法分析

常规嵌套阵列利用自协方差矩阵产生的虚拟阵列存在冗余阵元，需要对产生的虚拟阵列进行去冗余处理。去冗余后的虚拟阵列信号为相干等价信号，需要进行解相干处理。对于M个阵元的二级嵌套阵列，采用空间平滑[23]、矩阵重构等方法进行解相干处理后，可估计的最大信源数Kmax为

(40)

根据(13)式、(20)式可知，本文所提算法利用M个阵元二级嵌套阵不同子阵信号的互协方差矩阵生成了无冗余阵元的虚拟阵列，消除了噪声。针对虚拟阵列等效信号转化为相干信号，本文利用虚拟阵列及其共轭矩阵构造满秩的等效协方差矩阵实现了解相干，由[23]式、[24]式、[30]式、[31]式可知，可估计的最大信源数为M2/4+M/2-3/4，与利用自协方差矩阵的嵌套阵列最大可估计信源数相同，优于文献[16]、文献[18]、文献[19]中可估计的最大信源数M-1.

通过以上分析可知，本文所提算法的主要计算复杂度包括互协方差矩阵运算、矩阵奇异值分解、最小二乘法，所提算法涉及到的复数乘法次数为O[(M+1)2L/2+4((M+1)2/4-1)3+3k2(M+1)+3k3，其中k表示信源数，L表示快拍数。文献[16]利用互协方差矩阵进行联合奇异值分解(JSVD)算法需要波束形成进行角度搜索，假设搜索范围为[0°,180°]，搜索步长为0.01°，其算法复杂度为O[M2L+8M3+18 000M2]；文献[18]中所需的复数乘法次数为O[M2L+3M3+2M4]；文献[19]中所需的复数乘法次数为O[M2L+2k3+(7M-4)k2+k(M-1)(2M-k)]。

图2所示为本文所提算法与文献[16]、文献[18]、文献[19]所提算法的复杂度对比图。从图2中可以看出，本文所提算法无需进行角度搜索，计算复杂度低于文献[16]。但由于产生了更多的虚拟阵元，增大了角度自由度，本文所提算法的计算复杂度高于文献[18-19]。

图2 算法复杂度与阵元个数关系Fig.2 Algorithm complexity versus number of array elements

3 仿真实验及性能分析

为了验证本文方法的有效性，本文进行系列仿真实验，分析比较本文所提算法以及文献[16]、文献[18]、文献[19]中算法的估计性能，仿真实验中阵元间隔为半波长。采用均方根误差、角度分辨概率衡量DOA估计性能，如(41)式、(42)式所示：

(41)

(42)

为了验证所提算法的有效性，下面通过仿真实验分别分析所提算法的DOA估计性能、DOA估计性能与信噪比的关系，以及DOA估计性能与入射信源数的关系。

1) 仿真1.x轴方向阵元和y轴方向阵元个数均为9，子阵1～子阵4的阵元个数均为5，3个独立窄带远场的信号入射到阵列上，其入射信号角度(α,β)分别为(20°,10°)、(50°,40°)、(60°,50°)，快拍数为100，信噪比SNR分别为0 dB、5 dB、10 dB，进行200次Monte Carlo仿真实验。

图3、图4、图5分别表示信噪比SNR为0 dB、5 dB、10 dB时本文所提算法的估计结果。从图中可以看出，在信噪比分别为0 dB、5 dB、10 dB时，本文所提方法均成功实现了空间信源的方向估计，表明该算法可以在低信噪比环境下有效地进行DOA估计。

图3 SNR=0 dB的估计结果Fig.3 DOA estimated results for SNR=0 dB

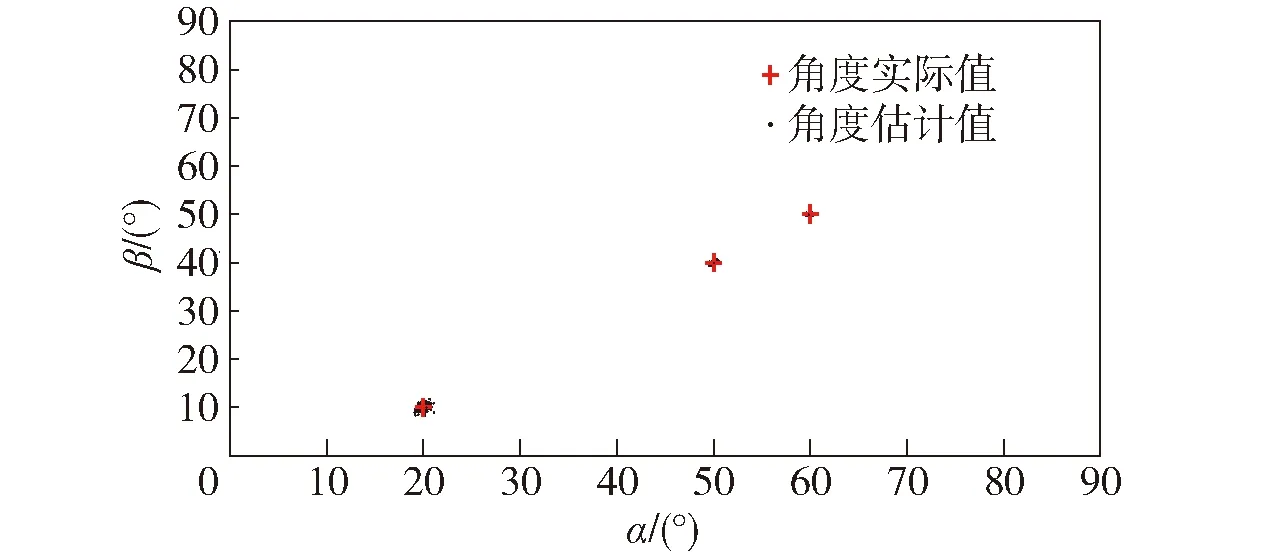
图4 SNR=5 dB的估计结果Fig.4 DOA estimated results for SNR=5 dB

图5 SNR=10 dB的估计结果Fig.5 DOA estimated results for SNR=10 dB

2) 仿真2.x轴方向和y轴方向阵元个数均为9，子阵1～子阵4的阵元个数均为5，3个独立窄带远场信号入射到阵列上，其入射信号角度(α,β)分别为(25°,10°)、(50°,45°)、(60°,55°)，信噪比SNR为0～20 dB，进行200次Monte Carlo仿真实验。图6所示为本文所提算法以及文献[16]、文献[18]、文献[19]算法的DOA估计均方根误差与信噪比的关系图。图7所示为本文所提算法以及文献[16]、文献[18]、文献[19]算法的角度分辨概率与信噪比的关系图。

图6 均方根误差与信噪比关系图(快拍数为100)Fig.6 RMSE versus SNR (Snapshots=100)

图7 分辨概率与信噪比关系图(快拍数为100)Fig.7 Angular resolution probability versus SNR (Snapshots=100)

从图6、图7中可以看出，本文所提算法的DOA估计均方根误差远小于文献[16]、文献[18]、文献[19]算法，而角度分辨概率分别优于文献[16]、文献[18]、文献[19]算法，表明本文所提算法的DOA估计性能优于文献[16]、文献[18]、文献[19]算法。当信噪比SNR=0时，本文所提算法的均方根误差小于1°，角度分辨概率接近90%，表明本文所提算法在低信噪比环境下具有较高的估计性能。随着信噪比SNR的升高，本文所提算法与文献[16]、文献[18]、文献[19]算法相比，其均方根误差变化较为平缓，表明本文所提算法对空间噪声具有更强的鲁棒性。

3) 仿真3.x轴方向和y轴方向阵元个数均为9，子阵1～子阵4的阵元个数均为5，入射到阵列上的信源数为1～10，入射角度(α,β)依次为(25°,30°)、(35°,40°)、(45°,50°)、(55°,60°)、(65°,70°)、(75°,80°)、(85°,90°)、(95°,100°)、(105°,110°)、(115°,120°)，信噪比SNR为10 dB，快拍数为100，进行500次Monte Carlo仿真实验。图8所示为本文所提算法以及文献[16]、文献[18]、文献[19]算法的DOA估计均方根误差与入射信源数的关系。

图8 均方根误差与入射信源数的关系图 (快拍数为100)Fig.8 RMSE versus number of incident signals (Snapshots=100)

从图8中可以看出，随着入射信源数从1增加到4，文献[16]、文献[18]、文献[19]算法与本文所提算法的DOA估计均方根误差均增大。在入射信源数大于5、小于8时，文献[16]、文献[18]、文献[19]算法的可估计最大信源数为M-1=8，此时入射信源数接近可估计最大信源数，算法的DOA估计均方根误差不随入射信源数的增大而增大。而本文所提算法的可估计最大信源数为M2/4+M/2-3/4=24，远大于仿真中入射信源数的变化范围，其DOA估计均方根误差随着入射信源数的增多缓慢增大，且本文所提算法的DOA估计均方根误差明显小于文献[16]、文献[18]、文献[19]算法，表明随着信源数的增多，本文所提算法的DOA估计性能优于文献[16]、文献[18]、文献[19]中的算法。当信源数为9、10时，入射信源数已经大于文献[16]、文献[18]、文献[19]算法的可估计最大信源数M-1=8，此时它们均已失效，而本文所提算法依然能够正常工作。

4 结论

本文针对L型均匀阵列角度分辨率较低、可估计空间信源数受限于阵元数及估计精度易受到信噪比影响的问题，提出一种新的L型嵌套阵二维DOA估计算法。该方法利用不同子阵信号的互协方差矩阵产生虚拟阵列并消除了噪声的干扰，利用虚拟阵列输出信号及其共轭矩阵构建了等效协方差矩阵，通过ESPRIT算法分别获得了角度α和β的估计值，利用虚拟阵列等效信源的唯一性实现了角度匹配。通过仿真实验，将本文所提算法与文献[16]、文献[18]、文献[19]算法进行了对比，仿真结果表明本文所提算法的估计性能明显优于其他算法，具有更大的角度自由度，可以辨识更多的空间信源，在低信噪比环境下具有较高的DOA估计精度。本文所提算法在获得更大角度自由度和更高估计精度的同时，不可避免地提高了算法的计算复杂度，在实际应用过程中需加以考虑。