基于独立电驱动履带车辆的地面参量估计方法研究

梁文利， 陈慧岩， 王博洋

(北京理工大学 机械与车辆学院， 北京 100081)

0 引言

影响混合动力履带车辆机动性和通过性的因素有很多，包括发动机功率、电机功率、车辆质量、履带宽度、履带接地长等。除了上述车辆参数与空气阻力的影响之外，地面条件也是影响履带车辆行驶性能的主要因素。

国内外很多研究者从速差转向车辆转向性能出发，建立了较为准确的履带车辆动力学模型，并对车辆性能进行了分析或对地面参量进行了估计。早在2004年，Martinez等[1]就提出了履带车辆的近似运动学模型并用于轨迹预测；程军伟等[2]考虑了履带车辆与地面之间的道路阻力系数和转向阻力系数，建立了较为准确的履带车辆滑移滑转模型。

车辆行驶数据往往能较准确地反映地面状况，因此对车辆行驶数据进行统计学分析，对于车辆- 地面系统的研究很有必要。文献[3]利用在线稀疏高斯过程表征某滑移转向的速度模型，并利用大量行驶数据对模型进行训练。文献[4]基于高斯混合- 隐马尔可夫模型的统计学习方法建立驾驶员模型，并利用模型对下一时刻车辆的转向模式做出预测。文献[5-8]通过构建运动基元的方式，对获得的大量试验数据进行分类，并与控制量相联系，从而输出控制序列。

地面参数是地面特征的直接体现，对地面参数进行准确估计是优化车辆行驶性能以及精确控制的基础。文献[9-10]提出的g算法可对3个土壤推力参数进行解耦和识别，并解决了利用贝克土壤理论进行地面参数估计所带来的多解问题[11-12]。文献[13]利用一套专用的测量装置，通过直接测量履带车辆两侧主动轮输出转矩的方法来计算履带车辆行驶地面行驶的参数值。文献[14]在不考虑滑移和滑转情况下，利用设计制造的履带模型车探究了松软草地上模型车车速对直线行驶阻力的影响规律。文献[15]根据地面力学理论对载荷比的影响因素进行了理论分析，并在车辆参数、行驶阻力系数一定条件下，通过土壤剪切试验获得了土壤参数值。文献[16]通过研究某滑移转向机器人平台不同转向半径下的稳态转向过程，实现了转向过程中地面参数的在线更新并建立了具有地面自适应性的车辆- 地面模型。

以上关于履带车辆地面参量估计的研究主要集中在以下两方面：一是基于贝克土壤理论的地面参数估值[9-12]，特点是涉及参数较多、计算量很大、效率低；二是通过设计专门的试验设备或测试系统，结合车辆动力学模型进行地面参量估计[13-15]，特点是试验过程复杂、精度不高。 基于此，本文提出一种依赖较少传感器进行地面参量估计的方法，通过对车辆行驶数据进行统计学分析，进而建立驱动力统计学预测模型的方法，并结合履带车辆动力学模型，对履带车辆行驶过程中的地面参量进行估计。

1 主动轮转矩预测值的生成

在进行地面参量估计过程中，首先需要提取车辆行驶数据，包括：采集时间t，左侧主动轮转速nl，右侧主动轮转速nr，航向角偏差Δθ，左侧主动轮转矩Tl，右侧主动轮转矩Tr(本文提到的左侧或右侧均为从车尾方向看；主动轮转速、主动轮转矩分别由电机转速、电机转矩以及电机与主动轮间的变速比求得)。通过路径分割和建立运动基元的方式对提取到的行驶数据进行重新分组，并建立相应的驱动力统计学预测模型，将驱动力统计学预测模型与车辆动力学模型相结合进行地面参量估计。算法具体流程图如图1所示。

图1 算法流程图Fig.1 Algorithm flow chart

由图1的流程生成主动轮转矩预测值，首先需要进行路径分割，然后基于路径段的聚类标签建立运动基元。

1.1 路径分割模型以及运动基元的建立

在建立运动基元模型过程中，如图2所示，先选取过零航向角偏差点作为路径分割节点进行路径分割，将车辆行驶路径划分为若干路径段，其中选取第i段路径的时间间隔td,i、平均航向角偏差Δθavei、最大航向角偏差Δθmaxi以及左主动轮平均转速nlavei，右主动轮平均转速nravei作为表征数据，具体表示为

pathi=[td,i,Δθavei,Δθmaxi,nlavei,nravei].

(1)

图2 路径分割以及运动基元的建立Fig.2 Path segmentation and establishment of motion primitives

利用高斯混合模型(GMM)对上述提取到的数据进行多元聚类，得到路径分割模型path. 多变量GMM可以表示为

(2)

式中：G(x)为变量x的高斯分布；K为路径段高斯分量的数目；pi为各高斯分量的先验概率值；

(3)

d为变量x的数据维度，利用极大似然估计和最大期望(EM)算法可得到各高斯分量的参数值，μi为各高斯分量的中心点矩阵，Σi为各高斯分量的协方差矩阵。

在建立GMM过程中 ，聚类个数以及聚类初始参数的确定十分关键。首先，选取不同行驶工况下的部分数据组成数据集Z，针对不同的聚类数目K，对Z进行多次K-means聚类，对于Z中的数据点i，计算其轮廓系数si，轮廓系数越接近1，说明对于该数据点的聚类结果越合理。计算Z中所有数据点的轮廓系数并求其平均值，选取平均轮廓系数最接近1的K值对应的聚类结果作为GMM的初始化参数。然后，利用EM算法对模型进行训练，从而得到需要的路径段GMM，其参数即为所求的pi、μi、Σi. 其中第i段路径的聚类标签可以表示为

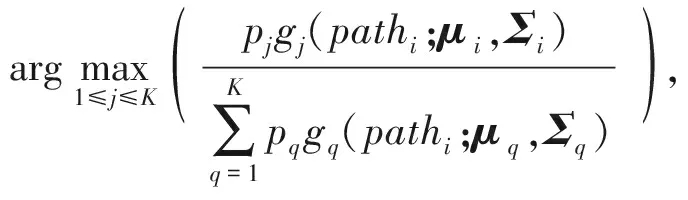
(4)

运动基元表示为

pathn=
[label_pathi-1,label_pathi,label_pathi+1]，

(5)

式中：1≤n≤K1，K1表示运动基元种类数。图3所示为运动基元的建立过程。

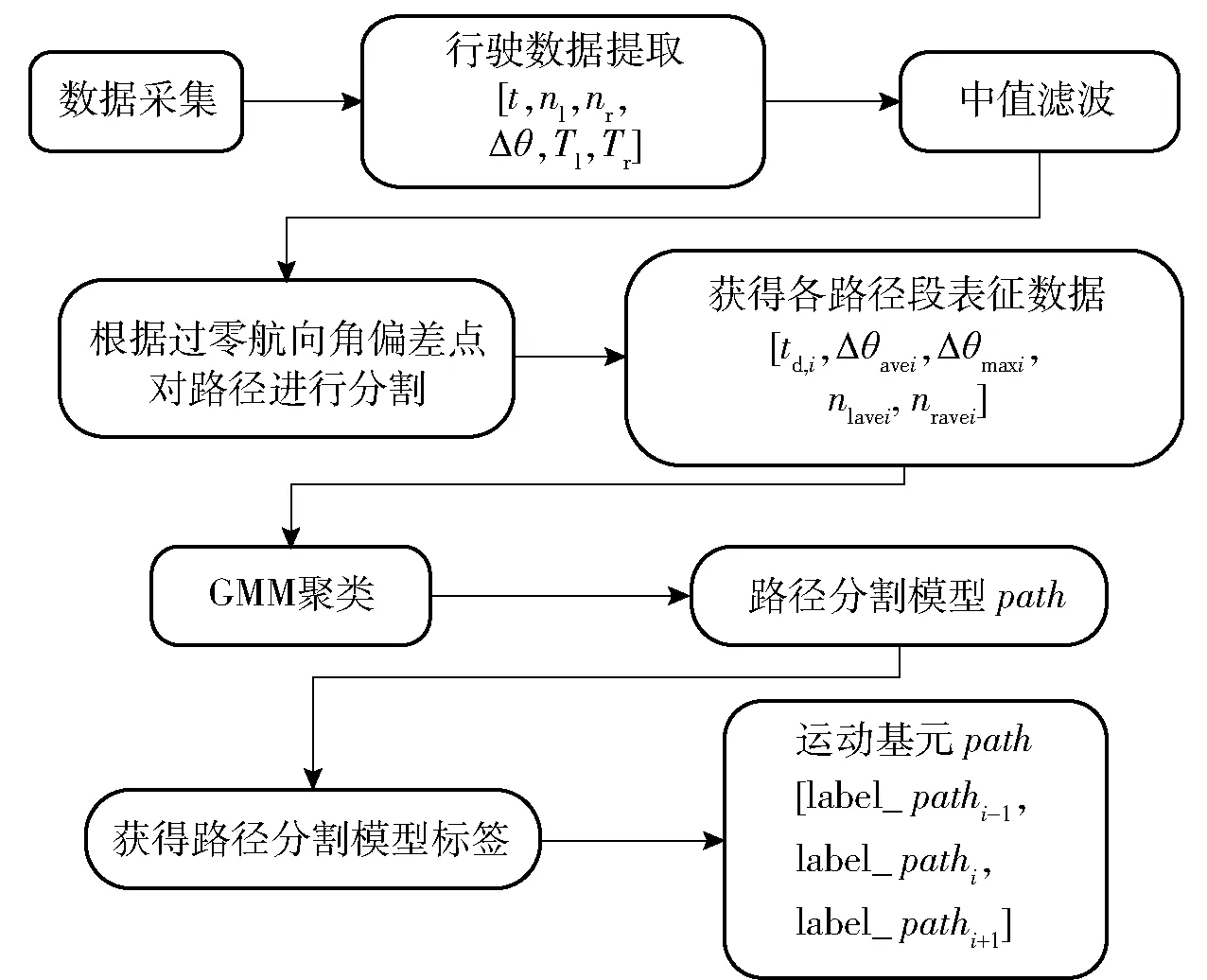
图3 运动基元建立过程Fig.3 Establishing process of motion primitives

1.2 建立驱动力统计学预测模型

在建立驱动力统计学预测模型过程中，以运动基元类型为依据对数据进行分组，基于分组后的数据，利用GMM构建驱动力统计学预测模型，因此建立的驱动力统计学预测模型与运动基元是一一对应的。驱动力统计学预测模型用到的车辆行驶数据以及表示形式为

Modeln=[nlΔtn,nrΔtn,ΔθΔtn,TlΔtn,TrΔtn],

(6)

式中：下标Δtn为训练集数据中第n类运动基元所占的总行驶时间；nlΔtn、nrΔtn、ΔθΔtn、TlΔtn、TrΔtn分别为Δtn时间范围内的两侧主动轮转速、航向角偏差以及两侧主动轮转矩，其中nlΔtn、nrΔtn、ΔθΔtn为模型输入，TlΔtn、TrΔtn为模型输出。利用GMM聚类建立驱动力统计学预测模型时，初始值确定和参数估计过程与1.1节相同。图4所示为驱动力统计学预测模型的建立过程。

图4 驱动力统计学预测模型建立过程Fig.4 Establishing process of driving force statistical models

驱动力统计学预测模型可看作在大量试验数据基础上建立的车辆- 地面关系模型，其中的输入量代表车辆系统，输出量受地面约束，与地面参数有关。当驱动力统计学预测模型以及输入量确定后，高斯混合回归(GMR)算法可以用来预测模型中的输出量，即两侧主动轮转矩。

1.3 基于GMR的主动轮转矩预测

当运动基元类型即n值确定后，就可确定对应的驱动力统计学预测模型，假设其聚类个数为K2，高斯分量k的均值矩阵和协方差矩阵则可以表示为

μk={μin,k,μes,k}，1≤k≤K2，

(7)

(8)

式中：μin,k、Σin,k、μes,k、Σes,k分别为输入值和估计值的均值矩阵和方差矩阵；Σines,k为输入值与估计值的协方差矩阵；Σesin,k为估计值与输入值的协方差矩阵。并且有

es,k=μes,k+Σesin,k(Σin,k)-1(Din-μin,k)，

(9)

es,k=Σes,k-Σesin,k(Σin,k)-1Σines,k，

(10)

式中：Din为输入量。

同时，对于输入量Din，其属于高斯分量k的概率为

(11)

最终输出量的预测值以及方差可以看作各高斯分量的混合，即

(12)

(13)

主动轮转矩预测过程如图5所示。

图5 主动轮转矩预测过程Fig.5 Predictiing process of driving wheel torque

2 地面参量求解过程

本文所研究的地面参量为行驶阻力系数以及转向阻力系数，在进行地面参量估计时，需要引入履带车辆的动力学模型作为主动轮转矩理论值的生成依据。下文中以下标i代表内侧履带，下标o代表外侧履带。

结合文献[2，17]，履带车辆两侧主动轮理论转矩与地面参量之间的关系可表示为

(14)

式中：Ti、To为两侧主动轮理论转矩；m为车辆质量；r为履带车辆主动轮半径；f为道路阻力系数；转向阻力系数μ=μmax/(0.925+0.15R/B)，R为转向半径，B为履带中心距，μmax为履带车辆转向半径R=B/2时的转向阻力系数；ai=Ai/(L/2)，ao=Ao/(L/2)，Ai、Ao分别为内侧、外侧履带转向极的横向偏移量，即内侧、外侧履带接地段的瞬时转向中心到内侧、外侧履带纵向轴线的距离，L为履带接地段长度；g为重力加速度；式中负号表示方向与车辆行驶方向相反。

假设根据驱动力统计学预测模型预测得到的两侧主动轮转矩分别为T′i、T′o，预测值个数为N. 利用非线性最小二乘法优化算法求解地面参数的流程如下：

步骤1根据(14)式，将含有f、μ的主动轮理论转矩表达式以及T′i、T′o代入(15)式：

(15)

地面参量求解过程如图6所示。

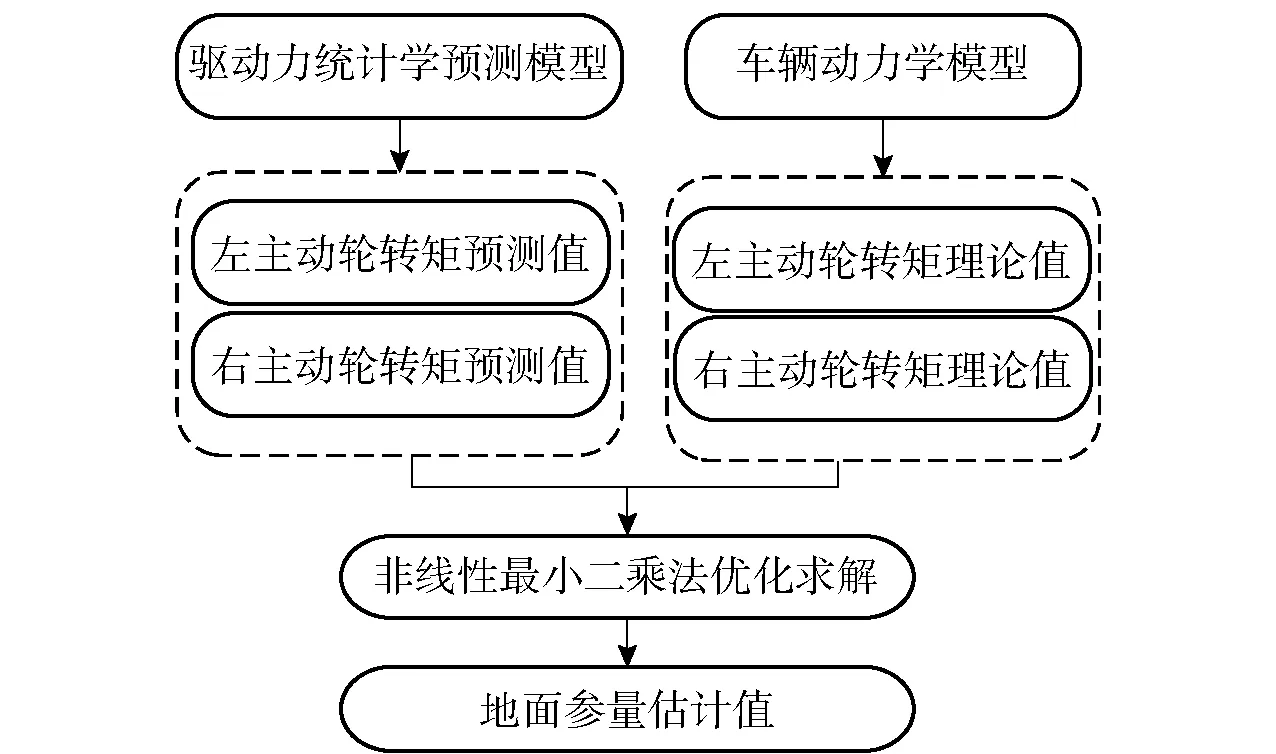
图6 地面参量求解过程Fig.6 Solving process of ground parameters

3 行驶数据分析

本文研究对象为独立电驱动履带车辆，由两侧电机带动主动轮，进而为车辆提供动力且两电机相互独立。为了得到某一路面对应的参数特性，采集履带车辆在该路面下不同行驶工况的数据，包括不同速度下的车辆直驶工况、S弯工况、换道工况、定半径转向工况等。为排除试验过程中的偶然误差，每类试验均重复多组，提取数据中的电机转速、车辆航向角以及电机转矩信息，其中电机转速以及电机转矩数据均为电机控制器的反馈量，航向角由惯性导航系统与全球定位系统组合定位系统测量得到。去除冗余数据(主要包括静止状态数据)并进行中值滤波处理；航向角偏差由下一时刻车辆航向角减去本时刻车辆航向角求得。将试验数据分为训练集和测试集，根据图3所示流程，利用训练集中车辆的过零点航向角偏差将路径分割为多个路径段，并进行GMM聚类，得到路径分割模型path，表1所示为路径分割模型的表征数据。

表1 路径段聚类结果

剔除出现概率较小的运动基元，建立的运动基元共分为8类，即K1=8，对应的路径段的标签组成以及所占比例如表2所示。

根据建立的运动基元对行驶数据进行重组，并根据图4利用GMM聚类建立相应的驱动力统计学预测模型。

为了验证驱动力统计学模型对两侧主动轮转矩的预测效果，根据图5所示流程，得到两侧主动轮转矩的预测值，将预测值与实际值进行比较，对比结果如图7和图8所示。

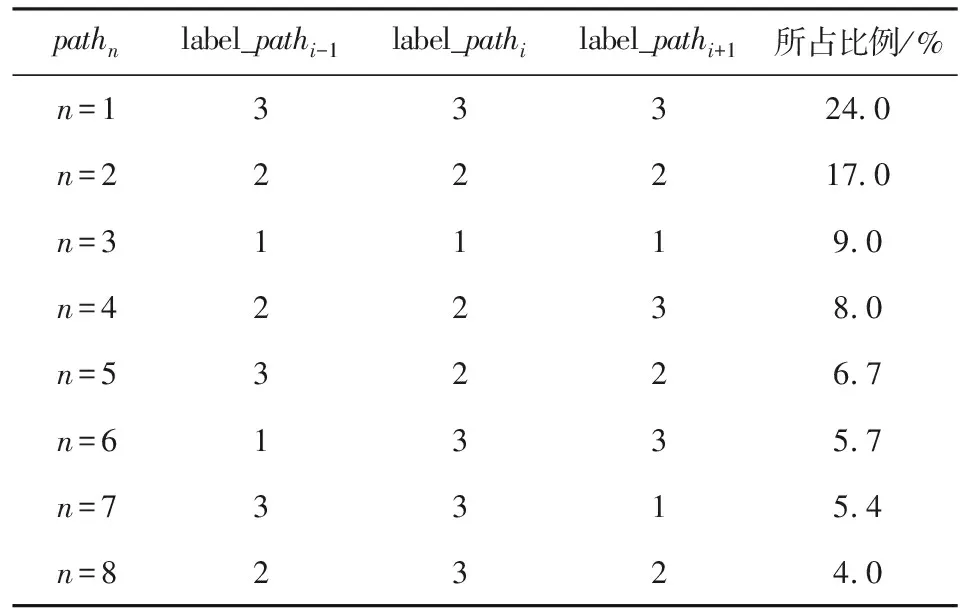
表2 运动基元生成结果

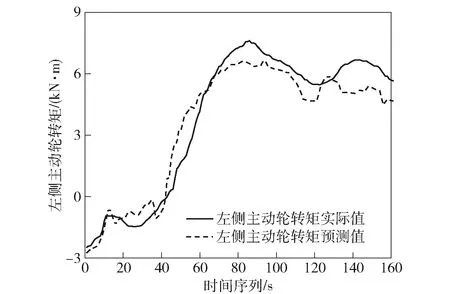
图7 左侧主动轮转矩预测值与实际值对比Fig.7 Comparison of predicted and actual values of the left driving wheel torque

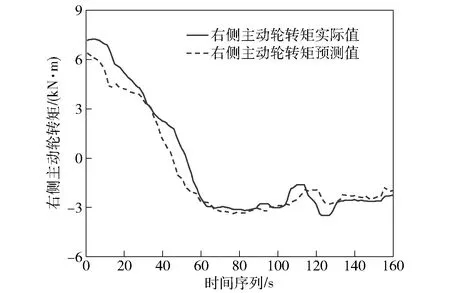
图8 右侧主动轮转矩预测值与实际值对比Fig.8 Comparison of predicted and actual values of the right driving wheel torque

由上述预测结果可知，本文所建立的驱动力统计学预测模型可以较准确地预测车辆在行驶过程中两侧主动轮转矩的变化。

4 实车试验

为了验证算法的有效性，在某平坦土路上(该路面与之前采集训练数据的地面一致)进行实车试验。试验车辆由某型号履带车辆改造而来，发动机通过燃烧燃油带动发电机工作，发电机将发出的电能与动力电池组中的电能进行混合，共同驱动两侧驱动电机，两侧驱动电机再通过2挡自动变速箱以及轮边减速器减速(自动变速箱1挡变速比为2.7，2挡变速比为1.0，数据均在1挡下采集；轮边减速比为5.5)，带动主动轮转动，最后推动平台运动。车辆总质量10 000 kg，履带接地段长度L=3.095 m，履带中心距B=2.464 m，主动轮半径r=0.265 4 m. 图9所示为试验车辆及路面。

图9 试验车辆及路面Fig.9 Test tracked vehicle and experimental road

试验过程中驾驶员操纵车辆，使车辆进行以下4种类型试验：

第1类：连续变半径转向试验，记录车辆行驶过程中的电机转速、航向角以及电机转矩。根据惯性导航系统与全球定位系统组合定位系统得到每一时刻车辆的经度和纬度坐标，经转换后得到某次试验中车辆的实际运动轨迹如图10所示。

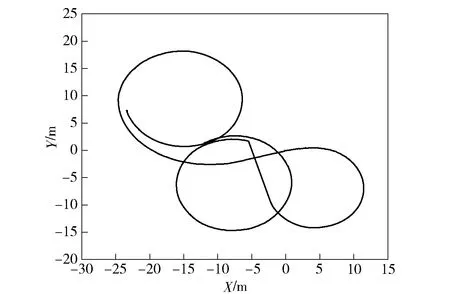
图10 连续稳态转向的车辆行驶轨迹Fig.10 Vehicle trajectory during continuous steady-state steering

第2类：直驶与大半径稳态转向试验，使车辆先直驶一段时间后进行较大半径的连续转向，某次试验中车辆的实际运动轨迹如图11所示。

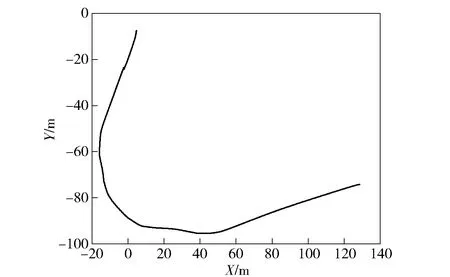
图11 直驶转大半径转向的车辆行驶轨迹Fig.11 Vehicle trajectory during straight driving and smooth radius steering

图12 一侧主动轮制动的车辆行驶轨迹Fig.12 Vehicle trajectory during driving wheel braking on one side

第3类：单侧履带制动的转向试验，使车辆保持一侧电机制动，另一侧电机保持恒定转速，车辆的实际运动轨迹如图12所示。

第4类：车辆滑行试验，车辆以某一速度匀速直线行驶一段距离后，将两侧电机切换至自由转模式，此时电机不再提供驱动力，根据滑行距离以及滑行前车速可以得到道路阻力系数f的测试值。试验数据如表3所示。

假设车辆进行稳态转向时两侧主动轮转矩实际值为T″i、T″o，将T″i、T″o代替T′i、T′o代入(15)式，利用最小二乘法迭代计算可得到转向阻力系数μ的测试值与转向半径R的关系。

根据图5所示流程，可以得到两侧主动轮转矩预测值T′i、T′o，结合第2节地面参数的求解步骤，可得到地面参数μ、f的估计值。μ、f的估计值与测试值对比如图13和图14所示。

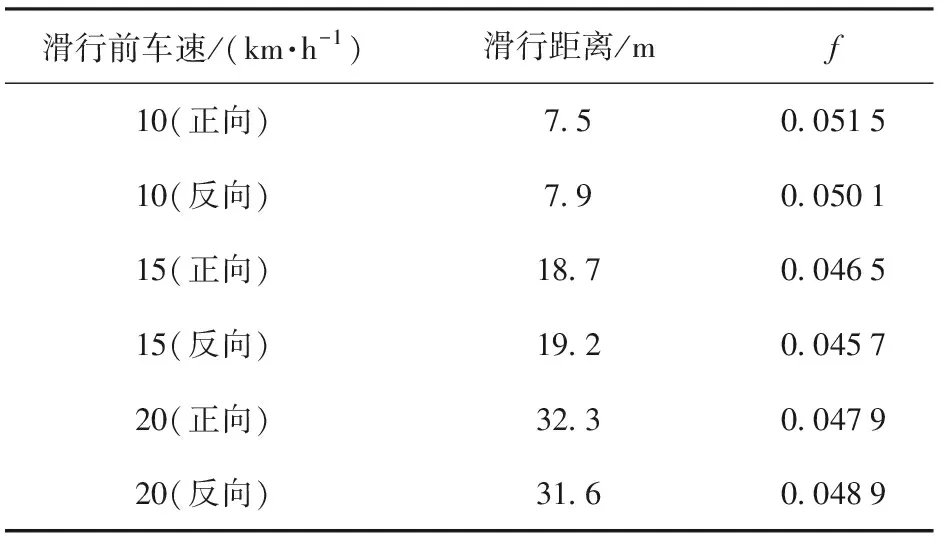
表3 滑行试验数据以及处理结果

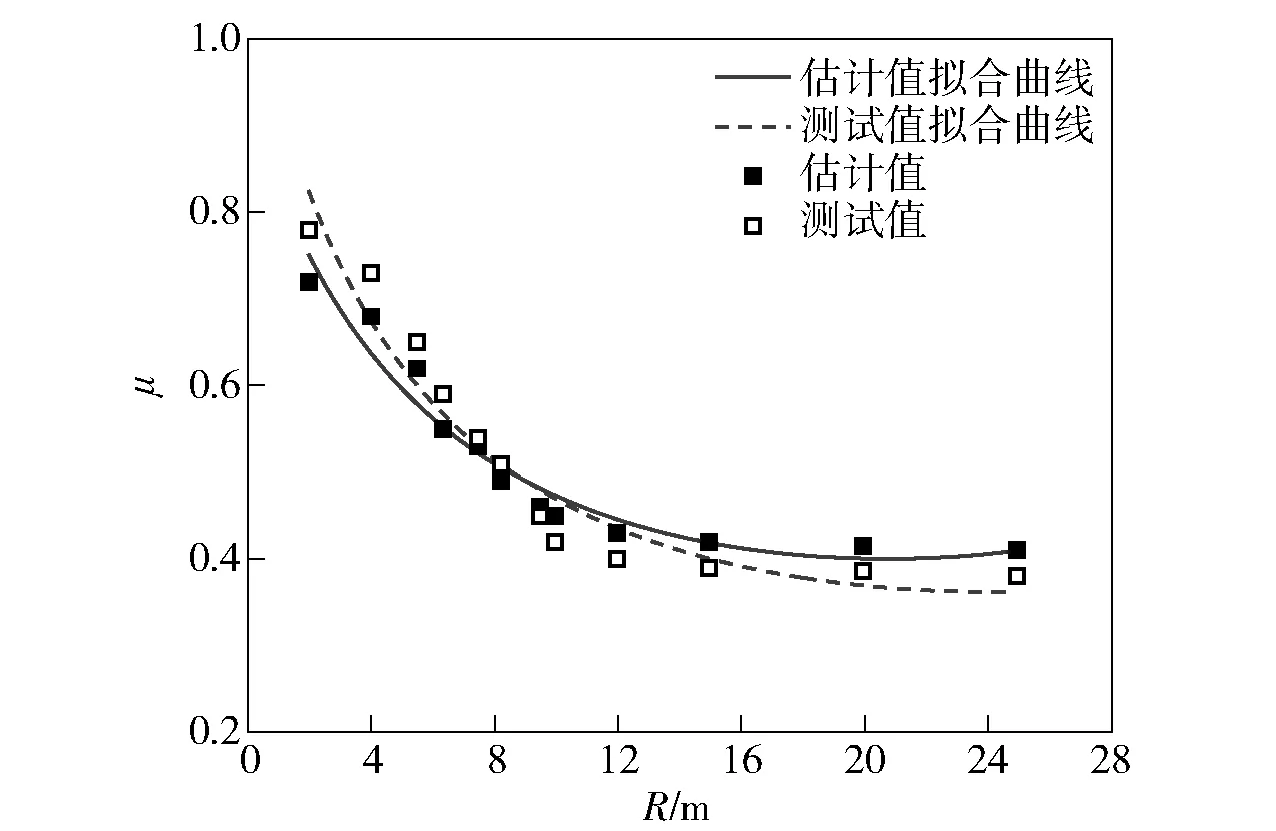
图13 转向阻力系数的估计值与测试值对比Fig.13 Comparison of estimated and test values of steering resistance coefficient

图14 道路阻力系数的估计值与测试值对比Fig.14 Comparison of estimated and test values of road resistance coefficient

由图13和图14可知， 本文提出的算法可以较为准确地对履带车辆行驶过程中的道路阻力系数和转向阻力系数进行估计。

5 结论

1) 以独立电驱动履带车辆的大量试验数据为依托，通过路径分割- 路径段聚类- 建立运动基元的方式，实现了对行驶数据的统计学表述。

2) 利用运动基元的种类对行驶数据重新分组，建立了对应的驱动力统计学预测模型，可对两侧主动轮转矩进行较准确的预测。

3) 驱动力统计学预测模型与车辆动力学模型相结合，对履带车辆行驶过程中的道路阻力系数和转向阻力系数进行了合理估计，其中转向阻力系数的估计误差低于10%，道路阻力系数的估计误差低于15%。

本文对于履带车辆的动力学研究具有一定参考意义，同时也可以进一步拓展到利用地面参量进行履带车辆的轨迹预测或者局部路径规划方面。