基于微小卫星合作博弈的失效航天器姿态接管控制*

罗建军，韩 楠，柴 源

(1. 西北工业大学 航天学院·西安·710072；2. 西北工业大学 航天飞行动力学技术重点实验室·西安·710072)

0 引 言

对失效航天器进行姿态接管控制提供一种回收和利用其上高价值有效载荷的方法，近年来得到了广泛的关注[1]。空间机器人与微小卫星提供了两种不同的实施失效航天器接管控制的方法。空间机器人的控制效率高，能够在较短时间内满足失效航天器的接管控制要求，但其研制成本高，任务设计复杂，且不适合于长期实施对失效航天器的接管控制。微小卫星具有研制周期短、发射成本低、任务设计简单的优点[2]，且能够通过与失效航天器形成组合体的方式，为失效航天器提供所需的控制力矩，以实现对失效航天器长期的姿态接管控制。近年来，国外航天机构提出了包括凤凰计划、iBOSS项目等在内的模块化航天器设计概念。未来，基于模块化设计的在轨组装航天器将具有适合于标准化设计的微小卫星对接接口。因此，微小卫星将能够为失效航天器的在轨服务与接管控制问题提供一种低成本、低复杂度的解决途径。

为了实现失效航天器的姿态接管控制，多颗微小卫星需要通过互相协同的方式，提供失效航天器姿态运动所需的控制力矩。目前，面向单个大型航天器的姿态控制问题已有很多研究[3-6]，其基本思路是先设计航天器的姿态控制器，并根据设计的姿态控制器来计算航天器姿态机动所需的控制力矩，最后将计算获得的控制力矩分配到航天器平台的多个执行机构上。基于这一思想，文献[7]面向多颗微小卫星接管控制失效航天器姿态运动的问题，提出了一种辨识控制一体化的设计方法，实现了在惯量参数不确定情况下的失效航天器姿态接管控制，但是该方法需要集中进行控制解算与分配，因而其容错性不足。文献[8]面向空间细胞机器人实施接管控制的问题，提出了一种分布式控制分配方法。其中，各细胞机器人通过自由拍卖和一致性协商实现了控制任务的分配，但文中没有考虑细胞机器人的控制约束问题。由于将姿态控制器设计与控制分配相结合的接管控制方法在每一时刻都要进行控制指令的分配，因此，接管控制任务在每一时刻都需要较大的计算量，设计一种能够避免控制分配的接管控制方法，将能够有效降低任务执行过程中的计算负担。

博弈论研究多参与者的最优决策问题，其中每一位参与者通过局部目标函数的优化获得控制策略[9]。通过合理设计博弈参与者的目标函数，可以在尽可能最大化参与者收益的情况下、通过各参与者的博弈决策完成博弈活动事先设定的全局目标。近年来，博弈控制方法在越来越多的实际工程问题研究中得到了关注和应用。文献[10]研究了无人机编队飞行的博弈控制方法。其中，各无人机通过独立优化经过合理设计的目标函数来进行自主协同控制，实现了考虑燃料均衡的编队飞行。在文献[11]中，多智能体通过独立进行目标函数的优化并获得控制策略，以非合作博弈的方式实现了碰撞规避。文献[12]通过博弈控制方法研究了无人机自主防碰撞的控制问题。文献[13]将博弈控制方法应用到了多智能体一致性问题的研究中。面向多颗微小卫星接管控制失效航天器姿态运动的问题，文献[14]设计了多颗微小卫星的微分博弈控制器。其中，各微小卫星通过独立进行局部目标函数优化的方式获得了各自的控制策略，能够在避免进行控制分配且尽可能使自身能量消耗最优的情况下实现对失效航天器的姿态接管控制。然而，由于各微小卫星仅追求自身局部目标函数的最优化，未能实现全局意义下的能量消耗最优。为尽可能减少执行姿态接管控制任务的微小卫星的整体能量消耗，本文研究了多颗微小卫星的合作博弈控制方法，并通过求解多颗微小卫星合作博弈的帕累托最优策略，进行了失效航天器的姿态接管控制。

本文的组织结构如下：第一节介绍了微小卫星合作博弈控制器的设计思路；第二节设计了能够实现失效航天器姿态接管控制的微小卫星局部目标函数，并在考虑组合体动力学约束、微小卫星控制约束的基础上建立了多颗微小卫星的合作博弈模型；第三节在考虑失效航天器跟踪时变期望姿态轨迹的情况下，研究了微小卫星合作博弈帕累托最优策略的求解问题；第四节通过数值仿真验证了微小卫星合作博弈控制方法的有效性；第五节给出了本文的结论。

1 设计思路

本文面向多颗微小卫星接管失效航天器姿态运动的控制问题，试图提出一种基于多颗微小卫星合作博弈的协同控制方法。

首先，面向失效航天器姿态接管控制任务的需求，设计能够使失效航天器跟踪期望姿态轨迹的微小卫星的局部目标函数

(1)

在式(1)中，tf为失效航天器姿态接管控制任务的终端时刻；xe为系统误差姿态状态量，其具体含义将在下文中给出；ui为微小卫星i的控制量；Qi>0、Ri>0均为对称矩阵。

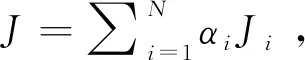
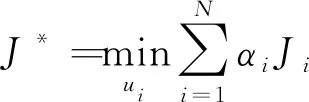
(2)

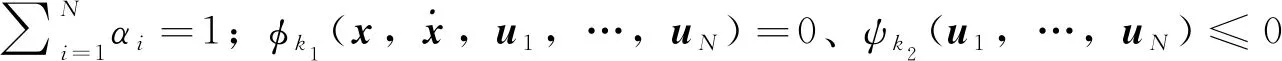
最后，通过构建由组合体误差姿态状态量与期望姿态状态量相对于时间导数所构成的增广姿态运动方程，将失效航天器跟踪期望姿态轨迹的任务要求转化为合作博弈控制优化问题中的动力学约束问题，并通过约束优化问题的求解获得各颗微小卫星的合作博弈控制策略，以在尽可能优化微小卫星整体能量消耗的前提下实现对失效航天器姿态运动的接管控制。

2 微小卫星合作博弈建模

失效航天器姿态接管控制过程会受到组合体的动力学约束及微小卫星控制约束。本节先给出组合体的动力学约束，之后建立考虑约束的微小卫星的合作博弈模型。

2.1 动力学约束

动力学约束由组合体的姿态运动方程给出。本文通过修正罗德里格斯参数(Modified Rodrigues Parameters，MRPs)来描述组合体的姿态运动，相应的姿态运动学方程为

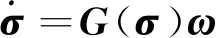
(3)

在式(3)中，σ∈R3为组合体的姿态MRPs，ω∈R3为组合体的姿态角速度，且有

(4)

组合体姿态机动所需的控制力矩完全由微小卫星提供，因此，组合体的姿态动力学方程为

(5)

在式(5)中，J∈R3×3为组合体的转动惯量矩阵；Cj∈R3×3为微小卫星j本体坐标系Ojxjyjzj(j∈N)到参考坐标系Oxyz的转换矩阵；Oj为微小卫星j的质心；xj、yj、zj分别为微小卫星j的3个体轴。本文选取微小卫星1的本体坐标系为参考坐标系。uj∈R3为微小卫星j的控制力矩。

根据组合体的姿态运动学方程和姿态动力学方程，可得组合体的姿态运动模型为

(6)

在式(6)中，x=[σT,ωT]T∈R6，且有

(7)

式(6)即为组合体动力学约束的表达式。

2.2 微小卫星合作博弈建模

任何一个博弈活动都由以下3个要素构成：博弈参与者N:={1,2,…,N}、各参与者容许策略集Ui、各参与者局部目标函数Ji[15]。为满足失效航天器跟踪期望姿态轨迹的任务要求，可设计如下的参与者(微小卫星)局部目标函数

(8)

当参与者进行非合作博弈时，便通过独立优化式(8)中的局部目标函数来获得控制策略。然而，由于非合作博弈难以实现全局意义下的目标函数最优，本文采用多颗微小卫星的合作博弈来进行失效航天器的姿态接管控制。

帕累托最优策略是一种典型的合作博弈最优策略，本文通过求解微小卫星合作博弈的帕累托最优策略来进行失效航天器的姿态接管控制。帕累托最优策略的定义如下：

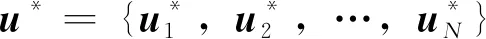
(9)

在式(9)中，Ui为微小卫星i的容许控制策略集。

帕累托最优策略为这样一个解，即任意的策略改变至少会使1位参与者的局部目标函数受到损失。

为求得微小卫星合作博弈的帕累托最优，考虑如下的各颗微小卫星局部目标函数的加权组合量

(10)

通过优化式(10)给出的微小卫星局部目标函数的加权组合量，便可获得微小卫星合作博弈的帕累托最优策略，并实现对失效航天器的姿态接管控制。

根据上述分析，可将失效航天器的姿态接管控制问题描述为如下的多颗微小卫星的合作博弈问题

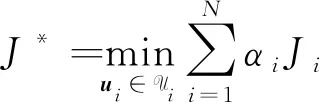
(11)

求解上述优化问题，便能获得N颗微小卫星的帕累托最优策略，以实现N颗微小卫星的合作博弈。

3 微小卫星合作博弈控制策略

失效航天器的姿态接管控制可分为姿态调节控制与姿态跟踪控制。姿态调节可认为是姿态跟踪的一种特例，即期望姿态轨迹始终保持为0。组合体的姿态运动模型本身具有较强的非线性，这使得微小卫星的合作博弈控制策略十分难以求解。此外，当失效航天器需要跟踪的姿态轨迹时变性较强时，微小卫星合作博弈的帕累托最优策略的求解难度将进一步增加。为此，本节首先给出了组合体的误差姿态运动方程，之后在合理设计组合体期望姿态轨迹的基础上，构造了由误差姿态状态量与期望姿态状态量相对于时间导数所构成的增广姿态运动方程，最后在考虑组合体动力学约束及微小卫星控制约束的前提下，研究了能够实现失效航天器跟踪时变期望姿态轨迹的微小卫星合作博弈控制问题。

令σe和ωe分别表示组合体的误差MRPs和误差角速度。根据文献[17]，有

(12)

误差MRPs相对于时间的导数为[17]

(13)

误差角速度为

ωe=ω-ωd

(14)

误差角速度相对于时间的导数为

(15)

为了进行组合体增广姿态运动方程的构造，将期望姿态状态的导数设计为期望姿态状态的函数，即

(16)

根据式(3)，期望MRPs相对于时间的导数为

(17)

记

(18)

(19)

在式(19中)

(20)

由于在跟踪时变姿态轨迹的任务中，仅要求控制xe至0，因此在微小卫星局部目标函数中不引入xd，其局部目标函数的加权组合量为

(21)

根据式(21)，可得如下的非线性约束优化问题

(22)

式(22)给出了能够满足失效航天器跟踪期望姿态轨迹任务要求的微小卫星合作博弈帕累托最优策略的求解框架。通过求解式(22)给出的约束优化问题，便可在不需要进行微小卫星控制分配的情况下直接得到能够实现失效航天器姿态接管控制的各颗微小卫星的合作博弈控制策略。

4 仿真算例及结果分析

本节通过2组数值仿真算例验证了将微小卫星合作博弈控制方法应用于失效航天器姿态接管控制问题的有效性。假设有4颗微小卫星进行失效航天器的姿态接管控制，其各自本体坐标系到参考坐标系的转换矩阵分别为

组合体转动惯量矩阵为

算例1假设期望轨迹为xd=[0,0,0,0,0,0]T，此时失效航天器跟踪期望姿态轨迹的接管控制问题变为了姿态调节问题。

假设组合体的初始MRPs为σ0=[0.2787,0.2036,0.7508]T，初始角速度为ω0=[0,0,0]T。选择微小卫星局部目标函数中的矩阵为：Q1=Q2=Q3=Q4=I6，R1=R2=R3=R4=0.2I3。全局目标函数中的可调系数为α1=α2=α3=α4=0.25。控制幅值为umax=0.5N·m，控制时长为tf=100s。

图1和图2分别为失效航天器姿态接管控制过程中组合体姿态MRPs和姿态角速度的变化曲线。由图1、图2可以看出，采用本文的合作博弈控制方法，多颗微小卫星通过合作博弈实现了失效航天器的姿态镇定。

图3给出了4颗微小卫星的控制力矩，其中绿色的虚线代表控制幅值约束。从图3可以看出，在整个姿态接管控制过程中，各颗微小卫星的控制力矩始终满足控制约束要求，且随组合体的姿态状态量逐渐逼近期望姿态状态xd，各颗微小卫星的控制力矩逐渐趋于0。

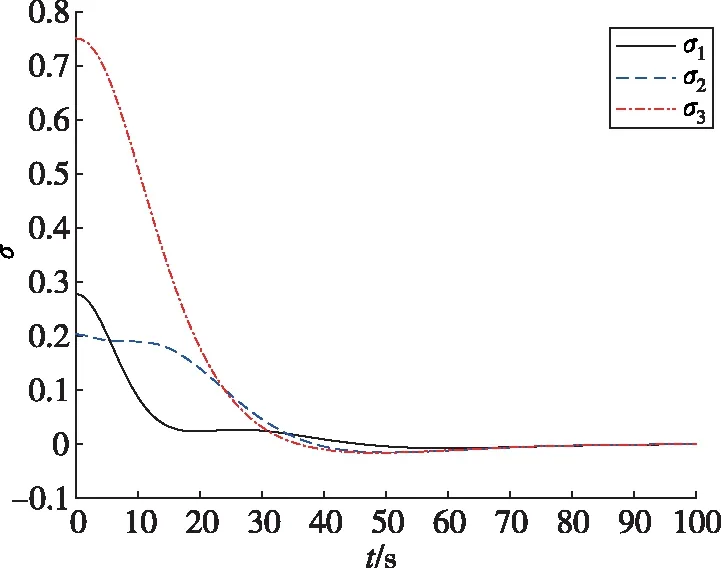
图1 组合体姿态MRPs随时间的变化曲线Fig.1 Attitude MRPs trajectories of combination

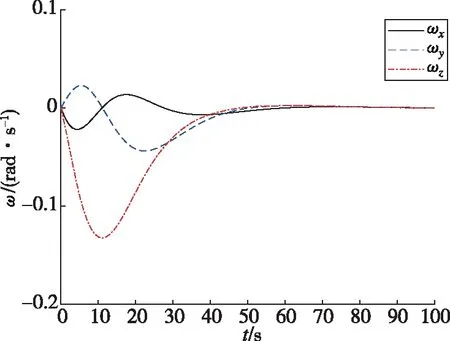
图2 组合体姿态角速度随时间的变化曲线Fig.2 Attitude angular velocity trajectories of combination

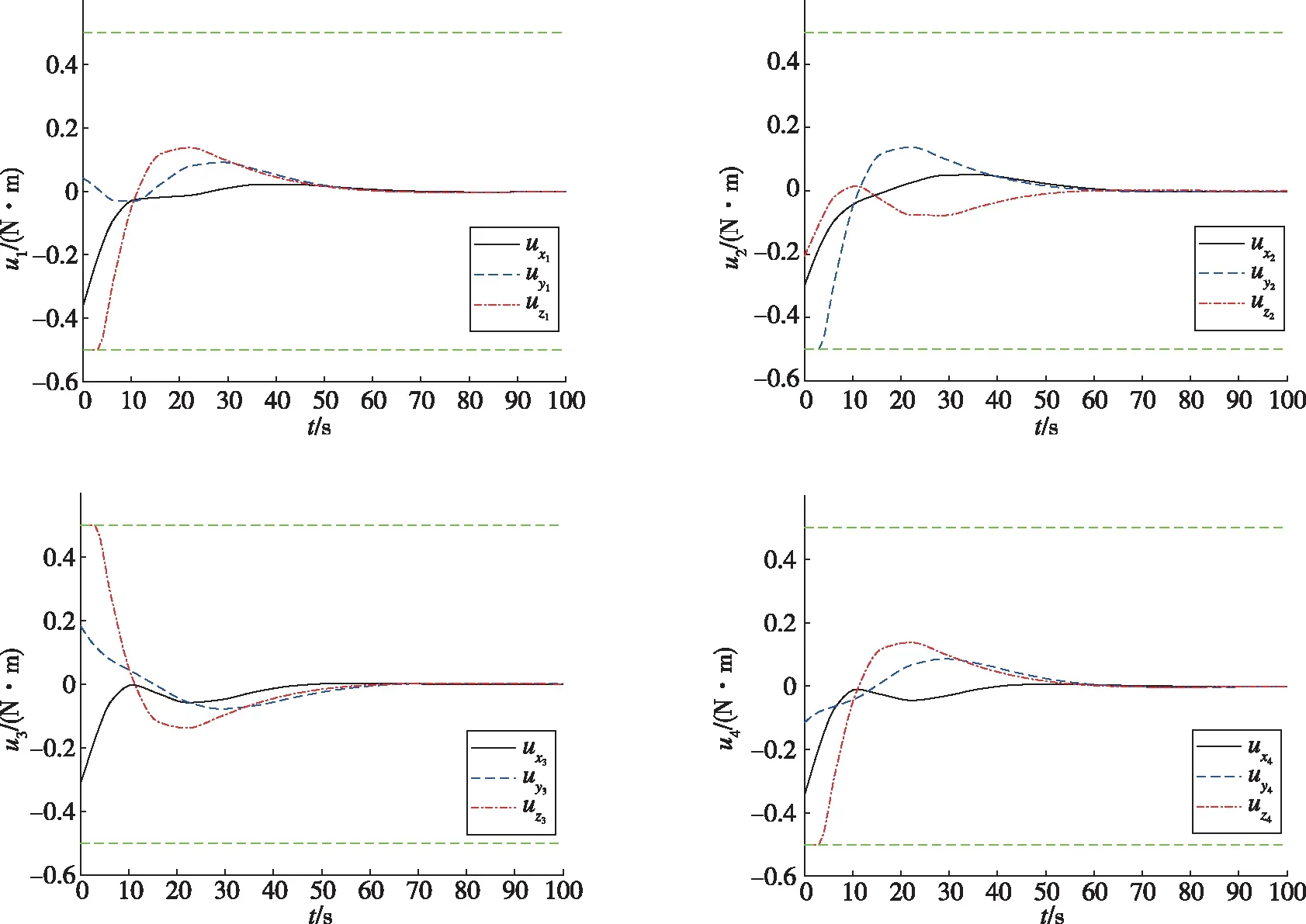
图3 微小卫星控制力矩随时间的变化曲线Fig.3 Control torques of microsatellites

算例2假设失效航天器的姿态角速度需要跟踪如下的期望轨迹

(23)

则期望角加速度为

(24)

其中

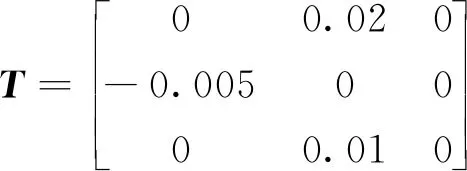
期望MRPs的初值为σd0=[0,0,0]T，给定期望角速度式(23)，期望MRPs轨迹可由式(17)得到。

假设组合体的初始MRPs为σ0=[0,0,0]T，初始角速度为ω0=[0,0,0]T。选择微小卫星局部目标函数中的矩阵为：Q1=Q2=Q3=Q4=400I6，R1=R2=R3=R4=0.2I3。全局目标函数中的可调系数为α1=α2=α3=α4=0.25。控制幅值为umax=0.5N·m，控制时长为tf=1000s。

图4和图5分别给出了组合体误差和期望MRPs随时间的变化曲线，可以看出通过文中的合作博弈控制方法，组合体的误差MRPs在初始20s内发生轻微变化后很快趋近于0。在图4中，误差MRPs在姿态接管控制任务刚开始时发生轻微变化的原因是在初始时刻，组合体的实际角速度ω0与期望角速度ωd0(ωd0=[0,0.05,0]Trad/s)不一致。为跟上期望角速度，组合体的姿态角偏离了σ0=[0,0,0]T。图6给出了组合体姿态MRPs随时间的变化曲线，其中绿色的虚线表示期望姿态MRPs轨迹。从图6可以看出，失效航天器在整个姿态接管控制过程中都较好地沿着期望MRPs的轨迹运动。图7和图8分别给出了误差和期望姿态角速度随时间的变化曲线。可以看出，通过文中的合作博弈控制方法，组合体的误差姿态角速度很快趋近于0。图9给出了组合体姿态角速度随时间的变化曲线，其中绿色的虚线表示期望姿态角速度轨迹，可以看出在整个姿态接管控制过程中，失效航天器都较好地沿着期望的姿态角速度轨迹运动。以上分析表明，多颗微小卫星采用合作博弈控制实现了失效航天器对期望姿态运动轨迹的跟踪。

图10给出了4颗微小卫星的控制力矩随时间的变化曲线。可以看出，为实现对期望姿态角速度轨迹的跟踪，在整个姿态接管控制过程中，各颗微小卫星都需要持续不断地为失效航天器提供控制力矩，但4颗微小卫星的控制力矩需始终满足控制约束的要求。

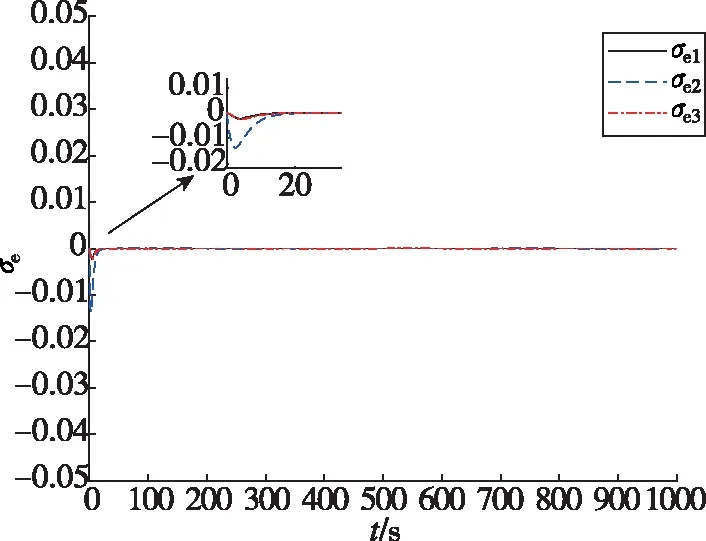
图4 组合体误差MRPs随时间的变化曲线Fig.4 Error MRPs trajectories of combination

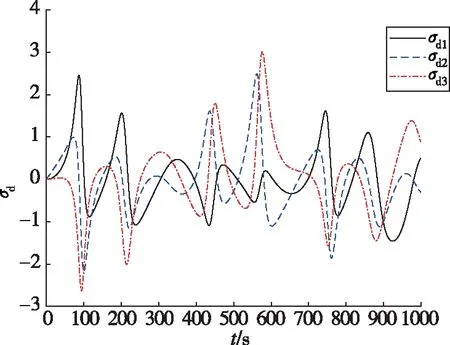
图5 组合体期望MRPs随时间的变化曲线Fig.5 Desired MRPs trajectories of combination

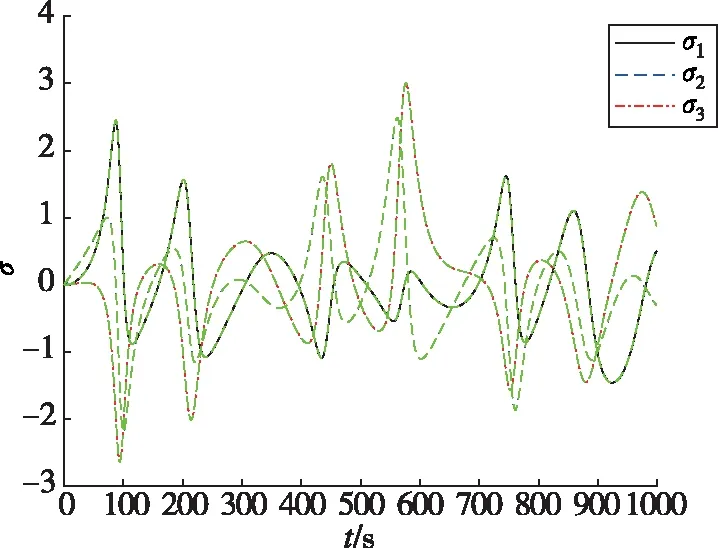
图6 组合体MRPs随时间的变化曲线Fig.6 MRPs trajectories of combination

图7 组合体误差角速度随时间的变化曲线Fig.7 Error angular velocity trajectories of combination

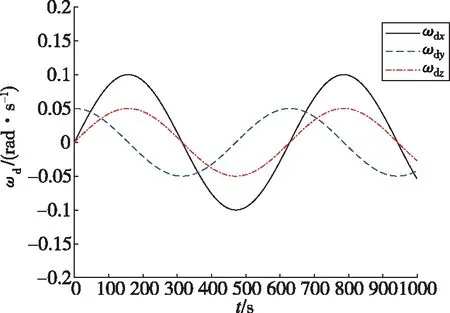
图8 组合体期望角速度随时间的变化曲线Fig.8 Desired angular velocity trajectories of combination

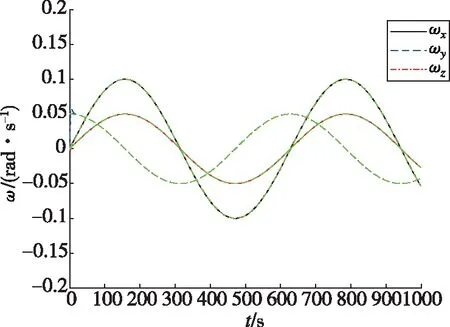
图9 组合体角速度随时间的变化曲线Fig.9 Angular velocity trajectories of combination

图10 微小卫星控制力矩随时间的变化曲线Fig.10 Control torques of microsatellites

5 结 论

本文针对多颗微小卫星协同完成失效航天器姿态接管的控制问题，通过合作博弈方法设计了微小卫星的协同控制器。文中面向失效航天器跟踪时变姿态轨迹的任务要求，合理设计了微小卫星的局部目标函数，并在考虑组合体动力学约束及微小卫星控制约束的情况下，通过优化多颗微小卫星局部目标函数的加权组合量，实现了对微小卫星合作博弈的数学描述。通过将失效航天器跟踪时变姿态轨迹的任务要求转化为1组由增广姿态运动方程描述的约束条件，得到了能够实现失效航天器跟踪期望姿态轨迹的微小卫星合作博弈问题的求解框架，从而能够在不需要进行控制分配的情况下实现失效航天器的姿态接管控制。数值仿真验证了本文设计的微小卫星合作博弈控制方法的有效性。本文未考虑微小卫星的能量均衡问题，后续研究将进一步考虑能够实现微小卫星能量均衡的博弈控制问题。