宽温域下三位四通电磁液动换向阀的几何尺寸链与卡滞特性*

訚耀保，谢帅虎，原佳阳，何承鹏

(同济大学 机械与能源工程学院·上海·200082)

0 引 言

滑阀是液压阀的一种重要结构形式，其通过滑阀副中的阀芯和阀套(或阀体)之间的相对运动改变节流口的面积，进而控制液压系统的流量或压力。由于结构简单、加工制造方便、原理清晰，滑阀在实际装备中的应用十分广泛。同时，正是由于滑阀应用的广泛性，一些在航空航天、高温、高压、高污染环境下服役的滑阀可能会出现卡滞、卡紧、动作延迟等问题，降低了整机工作的可靠性和稳定性。随着服役时间的延长，阀芯阀套的配合质量会出现下降，其控制性能的降低会引发压力脉动[1]。卡滞问题引起了国内外许多学者和工程技术人员的关注，相关科研人员做了许多工作并取得了很多成果。

阀芯卡紧的原因包括驱动力不足、油液污染、热变形等。根据滑阀结构和系统特性，可建立滑阀的动力学方程，并分析滑阀的静动态特性[2]；当温度变化时，油液黏度及阀开度、槽口深度和宽度等尺寸均会发生变化，并可能影响油液流动及配合特性[3]。从优化控制的角度，可利用传感器检测阀芯动力学行为与卡滞的关系，并根据这种关系校正控制器的控制特性，从而避免卡滞。仿真案例已验证了此方法的有效性[4-5]，文献[6-7]则详细讨论了卡滞的定义、建模方法和检测技术。

滑阀的阀芯和阀套为间隙配合，此间隙确保了滑阀副的平稳运动。滑阀副的平稳运动与泄漏是一对矛盾，平稳运动要求配合间隙大，但大的间隙导致泄漏量较大，反之亦然。虽然配合间隙是滑阀的重要参数，但在滑阀的设计过程中间隙值往往根据经验确定，缺乏定性分析依据和定量理论分析。考虑到滑阀工作环境的复杂性，在航空环境的高温高压工况下其配合间隙往往会发生变化，从而引起大的泄漏量或运动卡滞。目前的文献对滑阀泄漏和卡滞的综合考虑尚不全面。本文以某型飞机在运行环境中的滑阀作为研究对象，分析了温度、残余应力和油液压力引起的滑阀副配合间隙的变化量，并结合对泄漏量的要求，确定了合理的滑阀副配合间隙尺寸。

1 滑阀结构与工作机理分析

图1所示为滑阀的三维图，由阀套、主阀芯、差动阀芯组成。阀套为图1中的蓝色部分，主阀芯为图1中的红色部分，差动阀芯为图1中的透明部分。阀套固定在阀体上，阀套上的通油孔与阀体上的通油孔相连。主阀芯两端接控制腔，两端油液压力通过电磁铁实现控制。根据功能和结构划分，此滑阀是三位四通电磁液动换向阀。滑阀有3个工作位置，分别为中位、左位和右位。由于滑阀在右位时的工作状态与左位是一致的，因此本文仅分析滑阀在左位时的情况。

图2是滑阀工作在中位时的阀芯位置和油压分布，其中红色表示高压油液，蓝色表示低压油液。滑阀有4个通油口，分别为P(高压油源)、A和B(负载)、T(油箱)。滑阀工作在中位时，主阀芯两端的控制腔均为高压，主阀芯处于中间位置。由于差动阀芯凸肩的阻隔作用，P口的高压油液无法进入A、B两个负载端。同时，A、B负载端均与回油口T相连，故负载均为低压。当阀芯左端的控制腔由高压变为低压后，阀芯将向左移动，工作在左位。在阀芯移动的过程中，右边的差动阀芯被阀套阻挡，不会发生移动，但左边的差动阀芯则会被主阀芯推着向左移动。此时，P口高压油液进入B负载端，驱动负载运动。当左边控制腔再次变为高压后，虽然2个控制腔均为高压，但是右边差动阀芯与主阀芯之间为低压，因此主阀芯左端的受力大于右端。主阀芯向右运动直至回到中位时，两端受力达到均衡，主阀芯停止运动。

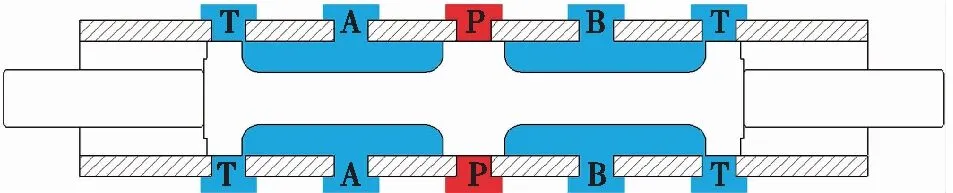
图2 滑阀工作在中位时的阀芯位置和油液分布Fig.2 The oil pressure distribution when valve is working in neutral position

根据对滑阀运动过程的分析可以发现，差动阀芯的存在使滑阀可以从左位移动到中位，但同时增大了滑阀结构的复杂性。一般滑阀仅含有1个滑阀副(1个配合面)，而此滑阀则含有3个滑阀副(3个配合面)，分别为主阀芯和差动阀芯接触面(配合面1)、差动阀芯和阀套接触面(配合面2)、主阀芯和阀套接触面(配合面3)。较多的配合面增大了内泄漏量，提升了运动的复杂度和加工难度。在实际工作环境中，此滑阀出现了卡滞和动作延迟现象，导致可靠性和稳定性降低，无法满足工作要求。为了解决滑阀卡滞问题，本文从由温度和由油液压力引起的滑阀副尺寸变形这两个角度进行了分析。

2 温度和残余应力对滑阀副尺寸链和配合间隙的影响

2.1 残余应力下滑阀副的热变形机理

由于热胀冷缩效应，不同温度下滑阀副的几何尺寸也会发生相应的变化。为了简化问题，将滑阀工作环境视为稳态均匀温度场，即温度不随空间和时间发生变化。根据热弹性力学可知，由温度引起的变形量可表示为

εr=εθ=εz=αT

(1)

在式(1)中，εr、εθ、εz分别为径向、切向和轴向上的线性应变分量；α为金属线膨胀系数；T为温度场的变化量。

滑阀副一般采用多种冷热加工方法加工而成，其制造过程不可避免地会产生加工应力。如果没有消除残余应力的措施或残余应力消除不完全，残余应力将会对滑阀副尺寸产生一定的影响。对于处于弹性变形范围内的金属材料，其应力应变关系符合广义胡克定律

(2)

在式(2)中，E为材料的弹性模量；σr、σθ、σz分别为物体微单元在径向、切向、轴向上的应力分量；μ为材料的泊松比。其中，弹性模量E不是恒值，其随温度变化的规律为

ET′=ET0[1+η(T′-T0)]

(3)

在式(3)中，ET0、ET′分别是温度为T0、T′时材料的弹性模量；η为材料弹性模量的温度系数。

装饰这个词，与我们的生活联系越来越紧密，也越来越受艺术家的重视，装饰性绘画在中国画中表现的越来越突出。在中国画中“意境”一直是画面的重要组成部分，水墨画主要是靠写意性来体现这一点的，工笔与写意是相对而立的，工笔画的意象趣味主要通过装饰性来表现。

根据式(1)～式(3)可知，由温度而引起的滑阀副尺寸变形存在两种机理，一个是热胀冷缩效应，另一个是改变滑阀副弹性模量进而改变应力变形量。由这两种机理引起的滑阀副变形量都是微小的，适用叠加关系，从而得到

(4)

由于要研究滑阀副配合间隙的变形，因此仅需关注阀芯阀套的径向变形，可忽略轴向变形和切向变形。阀套上有通油孔、倒角等细小结构，为了简化分析，可忽略掉这些细小的结构，将阀套简化为具有同心孔的金属圆筒，如图3所示。同样，可忽略阀芯上的凸肩和均压槽等细小结构，将阀芯简化为金属圆柱，如图4所示。

图3 同心金属圆筒Fig.3 Concentric mental cylinder

图4 实心金属圆柱Fig.4 Solid mental cylinder

根据方程式(4)，利用微积分方法，可推导出具有同心孔的金属圆筒的径向变化量和金属圆柱的径向变化量[8]，用公式可表示为

(5)

在式(5)中，uΔT1为圆筒半径为r处的径向变形量，uΔT2为圆柱半径为r处的径向变形量；a、b、c分别为圆筒的内外半径和圆柱半径；ΔT是温度变化量；σθa、σθb、σθc分别是表面a、b、c处的残余应力值。

2.2 滑阀径向配合间隙的变化

滑阀材料一般为9Cr18，其主要物理性能为：平均热膨胀系数α=17×10-6℃-1，泊松比μ=0.3，弹性模量的温度系数η=-25×10-5℃-1，在20℃时的弹性模量E=2×105MPa。阀芯和阀套在加工和热处理过程中不可避免地会产生残余应力，文献[9]介绍了各种加工工艺下的残余应力值。阀套一般采用淬火半精磨等工艺加工而成，残余应力值约为450MPa，方向指向圆心。阀套内孔一般采用精磨珩磨等工艺加工而成，残余应力值约为900MPa，方向背离圆心。由于阀套内孔空间狭小，在磨削时散热较差，容易发生由烧伤(非正常磨削)而产生的相变应力，此时残余应力值约为1200MPa，方向指向圆心。阀芯外圆一般采用淬火精磨等工艺加工而成，残余应力值约为850MPa，方向指向圆心。在磨削时，在砂轮变钝、进给量过大或冷却液不足等条件下(非正常磨削)，会发生烧伤而产生相变应力，此时残余应力值约为1200MPa，方向背离圆心。主阀芯凸肩、阀套内圆、差动阀芯外圆的公称直径为13mm，主阀芯芯轴和差动阀芯的内圆公称直径为6.5mm，阀套外圆的公称直径为17.8mm。将阀芯、阀套的几何尺寸和材料的物理性能数据代入式(5)，可得-55℃、100℃和150℃下的阀芯阀套径向尺寸及间隙相对20℃时的变化量，如表1所示。

表1 不同温度下阀芯阀套径向尺寸及间隙变化量(单位：μm)

从表1可以看出，在高温环境下，由于热胀效应，尺寸总是增大的，只是增大的量不同；在低温环境下，由于冷缩效应，尺寸总是减小的，只是减小的量不同。因此，残余应力并没有从根本上改变热胀冷缩效应。由于配合面的残余应力不一致，变形量不等，从而改变了配合间隙的大小。在高温时，正常加工的残余应力会增大配合间隙，如果加工不当，残余应力会减小配合间隙；在低温时，正常加工的残余应力会减小配合间隙，如果加工不当，残余应力则会增大配合间隙。在同一温度下，配合面3的变形量总是最大的。其中，在150℃时，配合面3的减小幅度最大，达到了2.9μm。

3 不均匀油液压力对滑阀副配合间隙的影响

阀套与阀体、阀套与阀芯之间存在密封关系。当通入压力油时，阀套内孔和外圆表面承受的液压力分布不均匀。在不均匀液压力作用下，阀套将发生微小变形，进而影响阀芯与阀套的配合间隙。如图2所示，阀体供油口处的高压油液作用在阀套外圆表面。由于滑阀阀芯与阀套的间隙密封，供油口位置对应的阀套内孔表面的液压力较低。此时阀套在液压力作用下发生轴对称的径向变形，导致间隙缩小，进而可能造成滑阀卡滞故障。为了分析这种由油液压力引起的阀套变形，直接计算是困难的，因此可采用有限元法进行数值计算。有限元法是计算零件变形的一种可靠手段，文献[10]即采用有限元法对飞轮转子及护套的压应力和热膨胀量进行了数值计算，计算结果与实验结果基本一致。下面对阀芯处于中位和左位两种状态进行分析。

3.1 滑阀阀套不均匀变形尺寸的有限元分析

在图1中阀套三维模型的基础上划分网格。静力学结构仿真对网格的要求不高，因此网格类型可选用非结构网格，网格尺寸为5×10-4m，划分结果如图5所示。

图5 网格划分结果Fig.5 Grids partition

阀芯处于中位时阀套受到的液压力如图6所示。在油液入口处，阀套外侧受到高压油液作用(图中以红色表示)。在阀套和阀芯的间隙处，油液处于层流状态。在同心环形缝隙流动中，油液压力均匀线性下降(图中以渐变色表示)。油液从配合间隙流出后进入A、B两个负载口，均为低压(图中以蓝色表示)。

图6 阀芯在中位时阀套的受力示意图Fig.6 Diagram of pressure distribution when valve is working in neutral position

阀芯位于左位时阀套受到的液压力如图7所示。同样地，在油液入口处，阀套外侧受到高压油液作用。油液进入阀套后，在阀芯的2个凸肩内的油液仍是高压。在阀套和阀芯的间隙处，油液压力均匀线性下降。油液从配合间隙流出后，变为低压。

图7 阀芯在左位时阀套的受力示意图Fig.7 Diagram of pressure distribution when valve is working in left position

3.2 仿真结果与分析

采用ANSYS WORKBENCH的静力学结构模块(Static Structural)作为数值仿真平台，油源压强为21MPa，回油压强为0.6MPa，阀套的2个端面为固定支撑面。仿真结果以变形量显示。图8是阀芯位于中位时的变形图。从图8中可以看出，油液入口处的阀套变形最大，沿径向的变形(指向中心)约为2.19μm。图9是阀芯位于左位时的变形图。从图9中可以看出，阀套最大的径向变形量为1.1μm，发生在P口和B口之间，但该处的变形方向背离圆心，即该处阀套向外膨胀。阀套最大的压扁变形同样发生在油液入口处，约为0.5μm。可以看出，不论阀芯位于中位还是左位，阀芯与阀套间的最小间隙都在减小，只是阀芯位于中位时的减小量更大。

图8 阀芯位于中位时的阀套径向变形云图Fig.8 Contour of sleeve’s deformation in radial direction when valve is working in neutral position

图9 阀芯位于左位时的阀套径向变形云图Fig.9 Contour of sleeve’s deformation in radial direction when valve is working in left position

4 滑阀卡滞及其解决措施

滑阀副的配合间隙在设计时应不小于滑阀副的变形量，否则间隙配合将变为过盈配合，易引起卡滞和动作延迟等不利现象。针对本文所研究的滑阀，由温度和残余应力引起的最大变形发生在配合面3，变形量为2.9μm。由油液压力引起的最大变形同样发生在配合面3，变形量为2.19μm。配合面1和配合面2仅受到温度和残余应力的影响，最大变形量为2.3μm。综合考虑温度、残余应力、油液压力三者的影响，配合面3的最大变形量为5.09μm。因此，在设计配合间隙时，需考虑到计算误差和加工精度，配合面3的配合间隙可取为5μm，配合面1和配合面2的配合间隙应在3μm以上。配合间隙的最大值应根据泄漏量确定。

滑阀副配合间隙为环形缝隙，因此泄漏类型为圆柱环形缝隙流动，流量泄漏公式为

(6)

在式(6)中，μ为流体的动力黏度；l为环形缝隙的长度；d为环形缝隙的直径(由于缝隙非常小，所以由d指代内径或外径均可以，本文取公称直径作为环形缝隙的直径)；δ为缝隙的大小；Δp为缝隙两端的压差。

此滑阀总共有3个配合面，因此存在3处泄漏。考虑到配合面1和配合面2的配合长度较长、存在节流槽，经实际计算后，发现配合面1和配合面2处的泄漏量比配合面3处的泄漏量小了一个数量级。因此，仅以配合面3的泄漏量作为确定配合间隙范围的参考值。阀芯位于中位和左位时的油液泄漏位置和流向可参考图6和图7。泄漏量受油液黏度影响，同时黏度又是温度的函数。不同温度下的油液黏度值可根据文献[11]确定。图10显示了泄漏量在不同温度下随配合间隙的变化。从图10中可以看出，中位时的泄漏量比左位时的泄漏量大。由于最大泄漏量需小于要求的泄漏量，因此根据中位泄漏量即可确定最大配合间隙。本文所研究的滑阀对泄漏量的要求是泄漏量不得超过0.035L/min。

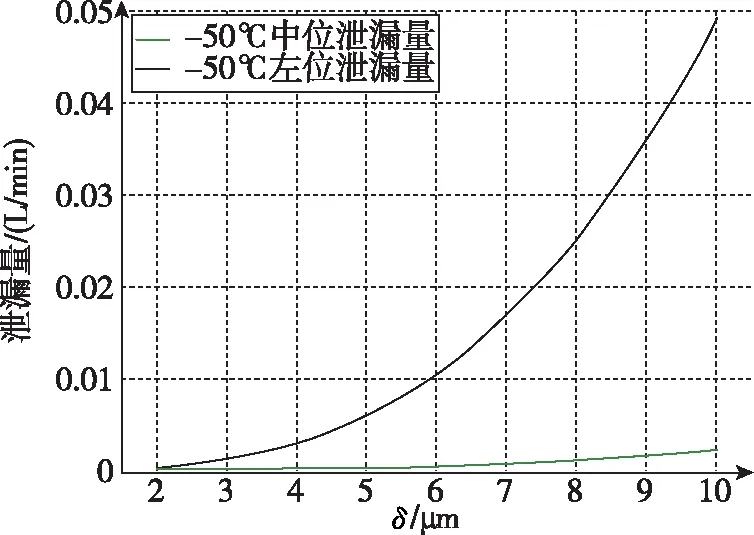
(a)-50℃时的泄漏量

(b)20℃时的泄漏量

(c)100℃时的泄漏量

(d)150℃时的泄漏量图10 滑阀间隙不同时的泄漏量Fig.10 Leakage versus radial clearance

在图10中，对应泄漏量为0.035L/min 的间隙分别约为8.7μm、6.0μm、3.7μm、3.4μm。从图10中得到的间隙为实际间隙(即将由油压和温度引起的变形考虑在内)，将实际间隙减去由温度和

油压引起的配合面变形量即可得到设计的间隙值。对应的变形量分别为-0.6μm、-2.2μm、-4.2μm、-5.1μm。因此，对应的设计间隙分别为9.3μm、8.2μm、7.7μm、8.5μm，设计间隙可取最小值(7.7μm)。考虑到加工精度，最终设计间隙可以近似定为8μm。从配合面1和配合面2泄漏的油液较少，因此最大间隙可根据加工方法确定。

5 结 论

本文针对在服役环境中某飞机的滑阀出现卡滞和动作延迟的问题，研究了由温度、残余应力和油液压力引起的滑阀副变形和尺寸链特征，并得出了如下结论：

(1)某型三位四通电磁液动换向阀，共有3个滑阀副。滑阀副的运动较为复杂。如果配合间隙设计不合理，容易引起卡滞、动作延迟等现象；

(2)滑阀在加工中不可避免地会出现残余应力。滑阀在较大温度范围内工作时，残余应力的释放显著引发了滑阀副阀芯阀套的不均等变形。提出了基于热变形和弹性力学理论建立滑阀副径向尺寸变形量的计算方法，既考虑了温度的热胀冷缩现象，又考虑了在温度变化时由残余应力释放而引起的滑阀副尺寸变形。针对所研究的滑阀及其服役环境，计算结果表明：在高温环境下，某型滑阀由正常加工造成的残余应力会增大滑阀副配合间隙；如果在磨削时发生烧伤，残余应力则会减小配合间隙。在低温环境下，则出现相反的效果。径向尺寸最大变形发生在150℃时主阀芯与阀套的配合面上，引发配合间隙减小了2.9μm；

(3)阀套内外表面受到的油液压力不等时，基于有限元方法的静力学结构分析结果表明：阀套在中位时的变形最大，变形量为2.19μm。泄漏主要发生在阀套与主阀芯凸肩的配合面处，并计算了不同温度下不同配合间隙下的泄漏量。计算结果表明，中位时的泄漏量远大于左位时的泄漏量；

(4)综合考虑温度、残余应力和油液压力对配合间隙的影响，结合对泄漏量的要求，对工作在极端温度(-50℃～150℃)、材料为9Cr18、阀芯公称直径为13mm的滑阀，提出了阀芯阀套配合面的径向配合间隙大于5μm时可避免卡滞、小于8μm时可满足泄漏量的要求。差动阀芯与阀套的配合面、差动阀芯与主阀芯的配合面的最小配合间隙为3μm，最大配合间隙可根据具体加工方法确定。