基于灰度预测的无刷直流电机控制*

尤 磊， 王 勇， 吴敬玉， 刘忠国， 周承豫， 乔永亮

(1.上海航天控制技术研究所·上海·201109； 2.上海惯性工程技术研究中心·上海·201109)

0 引 言

PID控制器因为其结构简单、成本较低、在简单系统中控制效果良好等优点，在工程实践中的应用十分广泛。但是，PID需要调节3个参数，即使应用较多的PI控制器也需要调节2个参数，其参数间的耦合关系较为复杂。目前，仍未有较为系统的参数调节方法。同时，确定的PID参数对于非线性、时延、负载变化的系统，在多数情况下无法实现理想的控制效果。飞轮使用的无刷直流电机，是典型的非线性、强耦合系统。为达到良好的控制效果，需要自适应调节的PID控制器，以实现较好的控制效果。

文献[1]将灰度模型G(1，2)与径向基函数(Radial Basis Function，RBF)神经网络控制结合起来，实现了小型无刷直流电机的智能控制；文献[2]和文献[3]使用灰度模型G(0，N)，将无刷直流电机模型分为确定部分和非确定部分，并设计为灰色模型，建立了参数在线调整的控制器，有效补偿了电机受到的干扰及非确定模型。由于采用了多输入方式，上述几种方法的实现较为困难；不使用电机双闭环控制中的电流环控制器，将导致电流无法快速响应指令，控制效果不佳。

本文建立了基于灰度模型G(1，1)的转速控制器，用于无刷直流电机的转速控制，电流环控制仍然使用了传统的PI控制器。由灰度模型预测电机在下一采样时刻的转速，建立预测误差值同PID参数间的变化关系，在线调整PID参数，以达到更加快速、稳定地跟踪预期转速指令的目的。

1 无刷直流电机模型

在飞轮中应用最多的是按Y形连接的三相无刷直流电动机。在无中线、忽略管压降的情况下，三相绕组的电势平衡方程为[4]

(1)

(2)

在式(2)中，LA、LB、LC为定子三相绕组自感；MAB、MBA、MAC、MCA、MBC、MCB为定子三相绕组间的互感。

假设三相绕组对称，不计磁路饱和的影响，则电子绕组电感(自感和互感)不随定子电流及转子位置而发生变化，即有

RA=RB=RC=Ra

(3)

LA=LB=LC=L

(4)

MAB=MBA=MAC=MCA=MBC=MCB=M

(5)

用Ra(a代表A、B或C)、L、M分别表示定子绕组的相电阻、相电感、相间互感，将式(2)代入式(1)并写为矩阵形式，可得

(6)

飞轮中的电机三相绕组为Y形无中线联结，则有

iA+iB+iC=0

(7)

因此

MiB+MiC=-MiA

(8)

将式(6)整理为

(9)

由于在实际应用中，习惯采用电动机线电压方程式，由式(9)可得

(10)

在式(10)中，eAB=eA-eB；eBC=eB-eC；eCA=eC-eA。

其中，各相绕组反电动势的幅值为

(11)

ea=KEω

(12)

产生的电磁转矩为

(13)

电机动力学模型为[5]

(14)

其中，Tl为负载转矩，B为阻尼系数。

2 灰度预测模型

灰度模型的常用符号为G(M，N)。其中，N表示变量个数，M表示常微分方程的阶数。在本文中，使用灰度模型G(1，1)预测无刷直流电机的转速。G(1，1)模型为1个输入变量的一阶灰度模型。由于其只有1个输入，因此结构较为简单，无需大量运算过程，采用一阶差分方式，利用较少的数据就可以得到较为准确的预测电机转速。

以下为建立转速灰度预测模型的过程：

(1)建立初始转速序列

ω(0)=[ω(0)(1)ω(0)(2) …ω(0)(n)]

(15)

在式(15)中，n为采集转速个数。该序列表示电机的实测转速值，用于预测下一时刻的转速，该序列最少需要4个数据[6]。所采集的数据越多，需要的计算量越大，相应的结果也越精确。在飞轮控制中，采用FPGA作为控制处理器。其资源有限，无法进行数量较多的灰度预测算法，因此选择4个数据对未来转速进行预测，即n=4。

(2)建立数据累加序列

ω(1)=AGO(ω(0))
=[ω(1)(1)ω(1)(2) …ω(1)(n)]

(16)

在式(16)中，ω(1)(k)表示数列ω(0)对应的前k项数据的累加，即

(17)

通过数据累加对测量转速的噪声进行简单的降噪处理，以加强数据的规律显现。

(3)建立背景值序列

k的取值为：k=2,3,…n

(18)

计算累加序列的平均值，防止原始序列自身存在突变的奇异数据而干扰模型，运用背景序列平滑这一阶跃特性。

(4)灰度差分方程

G(1，1)的一阶线性微分方程为

(19)

根据导数与差分的数学思想，可得

ω(0)(k)+az(1)(k)=b,k=2,3,…n

(20)

令

ω=[ω(0)(2)ω(0)(3) …ω(0)(n)]T

(21)

v=[ab]T

(22)

(23)

式(23)可写为ω=Bv，利用最小二乘法求解可得

(24)

(5)求解预测模型

求解式(19)，可得在第k+1时刻预测转速的累加值为[7]

(25)

则k+1时刻的预测转速值为

(26)

3 灰度预测控制器

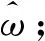
参数调节器的具体调整步骤如下

(1)计算预测误差函数

(27)

(2)定义预测精度函数

(28)

(3)PID输出控制信号

(29)

在式(29)中，eP、eI、eD分别为增益误差函数、积分误差函数，以及微分误差函数。

(30)

(31)

(32)

(4)采用梯度下降法求解参数

(33)

(34)

(35)

将式(27)、 式(28)、 式(29)代入式(33)、式(34)、式(35)，可得

(36)

(37)

(38)

(5)更新PID中的3个参数

(39)

(40)

(41)

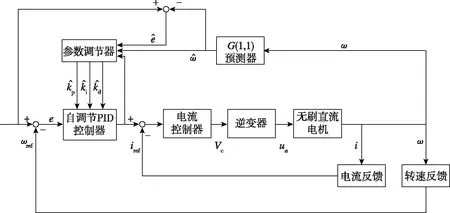
图1 基于灰度预测控制器的电机控制Fig.1 The control of BLDC motor based on Pray Prediction Controller

该控制器用预测误差代替实际误差，对传统PID中的3个控制参数提前进行了调整，应用梯度下降法使预测转速与理论转速的误差在最短时间内达到了最小值，从而求出了在每一时刻最合适的PID参数值。将该参数值应用于实际系统中，可使系统快速、稳定地达到预期状态。

4 仿真分析

在图1所示结构图中，针对电流控制器，仍然使用传统PI进行控制；PI控制器输出控制电压Vc，并在控制器内增加限幅，使得最大控制电压为Vcm；将Vc输入到逆变器中，通过整流作用，输出电机的相电压ua(a代表A、B、C)。作为具有时间滞后效应的增益环节，逆变器的模型如下

Kr·e-Tr

(42)

在式(42)中，

(43)

在式(43)中，Vdc为逆变器输入的直流母线线电压；fc为逆变器的开关(载波)频率。

由于在工程应用中，电机控制采用离散化方法，因此在仿真过程中，需对上述模型及控制律进行离散化处理。

仿真所使用的电机的参数如下：

逆变器输入的直流母线电压：Vdc=28V。

最大控制电压：Vcm=42V。

逆变器开关(载波)频率：4kHz。

电机三相电阻：Ra=0.3Ω。

电机三相电感：L=0.06mH。

忽略电机三相间互感，即M≈0mH。

电机转动惯量：J=0.088kg·m2。

电机电磁转矩系数：KT=0.38。

电机反电势系数：Ke=0.04。

图2为当电机给定转速为3000r/min时，电机转速从0r/min达到指定转速的2种控制器的表现；表1为2种控制器的具体性能指标。

图2 2种控制器控制效果的对比Fig.2 The contrast between two controllers

超调量稳态误差上升时间/s调节时间/s灰度预测控制器000.0490.049PID控制器9.7%00.0310.11

从图2和表1可以明显看出，灰度预测控制器比PID控制器能够更快、超调更小地达到转速理论值，实现对电机的智能控制。

图3为PID参数随预测转速的变化值。

(a)比例增益Kp的变化曲线

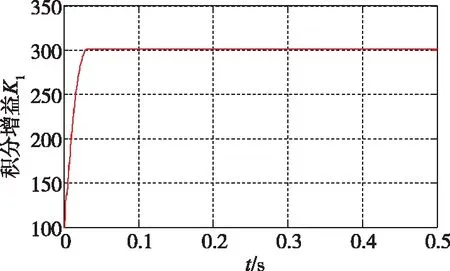
(b)积分增益KI的变化曲线

(c)微分增益KD的变化曲线图3 预测下的灰度预测控制器的参数变化Fig.3 The variety of parameters based on Gray Prediction Controller

为验证灰度预测下的电机抗干扰能力，在1s处对电机施加0.1N·m的干扰力矩。图4所示为在存在外力矩干扰下的电机的调节情况。从图4可知，灰度预测控制器受干扰后的偏差值为1.8%，PID控制器的偏差值同样为1.8%；但是，灰度预测控制器在0.079s后重新恢复稳定，而PID控制器则需要0.167s才可恢复稳定。因此可知，运用灰度预测控制器的系统抗干扰能力更强。图5所示为在干扰情况下灰度预测控制器的参数变化。

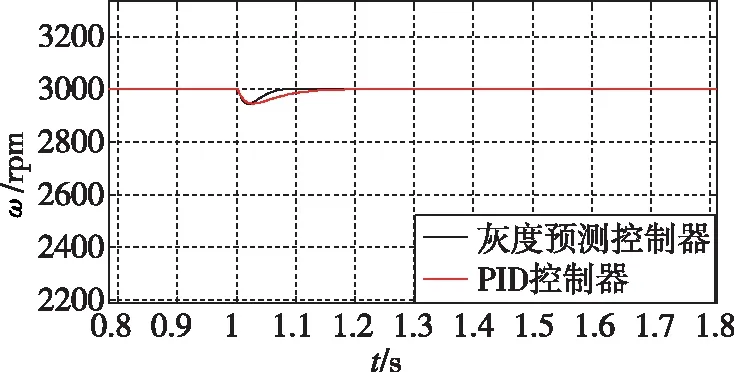
图4 负载干扰下的控制效果对比图Fig.4 The contrast between two controllers under loading

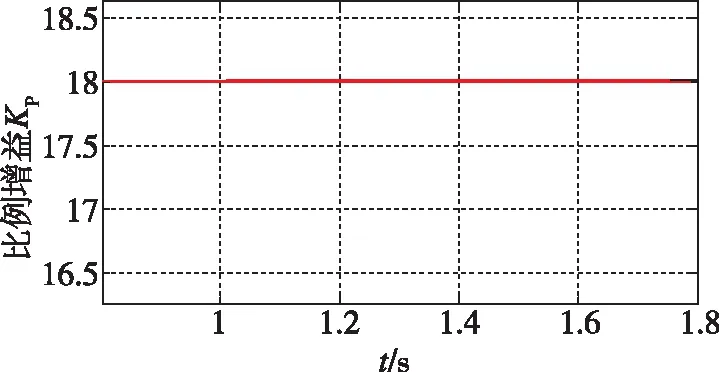
(a)比例增益Kp的变化曲线

(b)积分增益KI的变化曲线

(c)微分增益KD的变化曲线图5 负载干扰下灰度预测控制器的参数变化Fig.5 The variety of parameters under loading based on Gray Prediction Controller

5 结 论

本文设计了参数可调节的灰度预测控制器。该控制器将灰度预测模型G(1，1)和梯度下降法进行了结合，以求解PID的参数变化。灰度预测模型将下一采样时刻的转速较为准确地预测出来，通过梯度下降法寻找参数变化的规律，对任意给定的正实数参数均可实现快速响应的效果。

由仿真结果可知，相较于传统PID控制器，灰度预测控制器实现了无超调控制，调节时间减少了55.5%。同时，稳态误差为0，即准确地跟踪了转速指令。由此验证，用4个数据进行预测，可快速、平滑且准确地控制电机转速。对于外部突加干扰，灰度预测控制器可以更加快速地消除系统所受到的干扰。相对于传统PID控制器，其稳定性更强。由此，验证了该方法的有效性。