高超声速飞行器纵向系统鲁棒协调控制器设计*

牟金震，温凯瑞

(上海航天控制技术研究所·上海·201109)

0 引 言

高超声速控制系统设计的两个重大难题是系统的耦合问题与不确定性问题[1-3]。针对这两个问题，许多学者基于高超声速飞行器的纵向模型开展了相关研究。文献[4]对纵向模型输入输出进行了线性化，在此基础上设计了自适应滑模控制器与滑模观测器，使系统具有较强的鲁棒性。文献[5]忽略了纵向系统间的弱耦合，基于控制模型设计了鲁棒控制器，并提出了利用飞行器的鸭翼来提高系统的协调性。文献[6]对纵向系统的姿态模型进行了鲁棒性研究，针对攻角受限问题设计了反馈控制律。文献[4-6]针对飞行器纵向不确定性问题的研究均取得了较大的成果。针对纵向系统的耦合问题，文献[7]基于3D模型研究了纵向系统与推力系统间的耦合关系，并采用结构图的形式体现了系统的耦合关系。文献[8]将纵向系统的耦合归并为系统的不确定性来处理，基于动态逆设计了耦合观测器。文献[9-10]利用分层协调的思想，将纵向系统分解为高度回路、速度回路、姿态回路与推力回路，并针对不同回路分别设计了耦合补偿机制。文献[7-10]针对纵向系统的耦合问题的分析研究均取得了较大的成果，但对如何弱化耦合与补偿耦合的问题的研究仍然处于起始阶段。基于此，本文对纵向系统间的强耦合问题继续展开研究。本文主要研究的内容包括：(1)基于耦合度表征纵向模型变量间的耦合关系；(2)采用系统分层协调思想，将系统分为速度、高度/航迹角、攻角/俯仰角速率回路，即速度、高度与姿态子系统；(3)对于速度及高度子系统，采用耦合补偿的方法设计了协调控制器；(4)在姿态子系统中，通过耦合转换技术设计了协调因子，将“直接导数耦合”弱化为“间接导数耦合”，并设计了协调控制器。

1 高超声速飞行器纵向模型

飞行器的纵向模型可以描述为[7-10]

(1)

其中，系统状态变量x=[V,H,γ,α,q]，V为飞行器速度，H为飞行器飞行高度，γ为航迹角，α为攻角，q为俯仰角速率；输入变量为u=[φ,δe,δc]T，φ为燃料当量比，δe为升降舵，δc为鸭翼；输出变量为y=[V,H]T；T、D、L、m分别为推力、阻力、升力与俯仰力矩，M为飞行器质量。纵向气动力与力矩的表达式为

(2)

2 耦合度分析

为了表示纵向系统变量间的耦合关系，基于数学采样方法计算纵向系统间的耦合度[9-13]。下面给出了变量[H,V,γ,α,q]与[δe，δc，φ]的耦合度η、[H,V]与[γ,α,q]的耦合度χ，以及α与[γ,q]的耦合度σ，分别为

(3)

(4)

(5)

在耦合度矩阵(3)中，状态变量H与δc的耦合关系最强，与φ的耦合关系最弱；V与φ的耦合关系最强，与δe、δc的耦合关系基本一致；γ与δc的耦合关系最强；α与δe、δc的耦合关系基本一致；q与δe的耦合关系最强，与φ的耦合关系最弱。在耦合度矩阵(4)中，H与γ的耦合度最强，与α的耦合度次之，与q的耦合度最小；V与γ的耦合度较强，与其他两个变量的耦合度较弱。在耦合度矩阵(5)中，α与q的耦合度最强，与γ的耦合度较弱。

3 纵向鲁棒协调控制

纵向协调机制设计的基本思想是分层协调，首先，将整个系统分为速度子系统、高度/航迹角子系统，以及姿态子系统。每一层的协调基于本层的输入量、虚拟控制质量来完成，如图1所示。在速度子系统中，φ与V是最强的耦合，协调的目的是设计协调控制器φ以补偿此耦合。高度/航迹角子系统协调设计的第一步是设计γcmd，以协调H与V；第二步是设计αcmd，以协调γ与V；最后设计qcmd，以协调α与γ。在姿态子系统中，α与q的耦合关系可被描述为“直接导数”关系，协调的基本思想是引入协调因子，将“直接导数耦合”转换为“间接导数耦合”，以降低耦合效应。

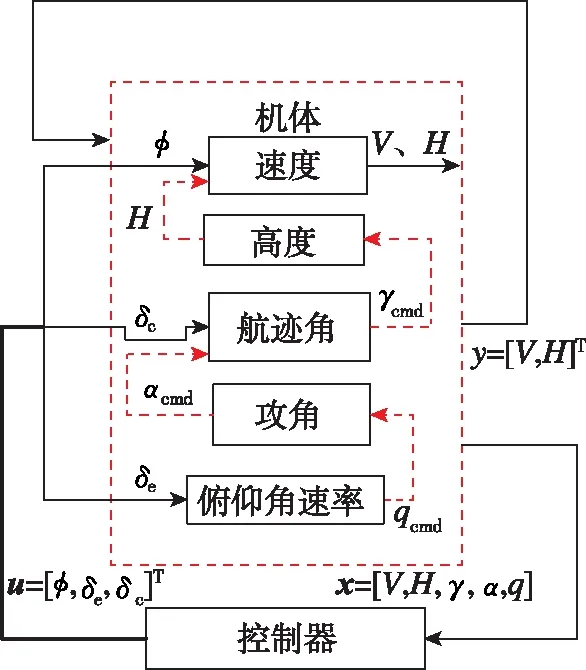
图1 纵向系统协调控制原理图Fig.1 Block diagram of the coordinated control architecture

将式(1)所给出的纵向模型表示为如下形式[5,15]

(6)

控制器的目的是对于给定的信号yref(t)=[Vref(t),Href(t)]T，其速度与高度能稳定跟踪参考信号，将协调指令设计为φ、γcmd(t)、αcmd(t)、qcmd(t)，将跟踪误差定义为

Href,γ-γcmd,α-αcmd,q-qcmd]T

(7)

3.1 速度回路鲁棒协调控制器设计

将推力T的表达式代入式(1)中的速度模型，可得速度回路误差的动态模型为

(8)

定义不确定参数θ1∈R16为

(9)

将式(9)代入到式(8)中，则式(8)可重写为

(10)

其中，B1(x)与ψ1(x,u,yref)的表达式为

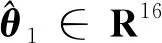
(11)

其中，Γ1∈R16×16是一个正对角矩阵。由投影算法可知[14-15]，速度子系统的控制律选择为

(12)

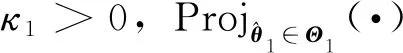
对式(11)的Lyapunov函数进行求导可得

(13)

注1：所有的气动参数均具有不确定性，为了控制器设计的方便，将CT,φ(α)、CT(α)、CD(α,δ)中的不确定参数分解为不确定参数矩阵θ1，因此式(8)可重写为式(10)。

3.2 高度/航迹角回路鲁棒协调控制器设计

(14)

(15)

对γcmd求导有

图2 高度/航迹角子系统控制系统的原理Fig.2 Schematic diagram of altitude and velocity subsystem control

(16)

由式(1)、式(2)有

(17)

(18)

则式(17)可以重写为

(19)

(20)

其中，Γ2∈R4×4是正对角矩阵。由式(19)可知，高度/航迹角子系统控制律的选择为

(21)

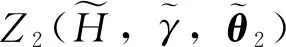
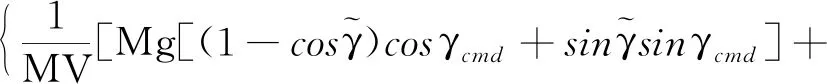
(22)

由于|γ-γcmd|≤9.17°，则有

(23)

此外，存在

(24)

其中，Ks是一个随时间变化的气动参数。由式(22)、式(23)、式(24)可得

(25)

其中，Kc是一个随时间变化的气动参数，kc是一个大于0的常数。因此，将式(23)、式(24)、式(25)代入到式(22)，有

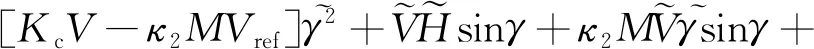
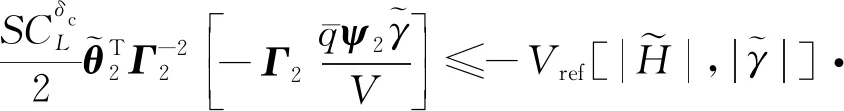
(26)

其中，

(27)

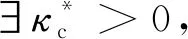
(28)

3.3 攻角/俯仰角速率回路鲁棒协调控制器设计

为了获取协调指令αcmd，由公式(1)，速度动态模型与航迹角的动态模型可以写成如下形式

(29)

其中，uV=Tcosα，uγ=Tsinα，则式(29)可转化为

(30)

因此，虚拟控制指令选择为

(31)

由此，期望的攻角指令信号设计为

(32)

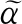
(33)

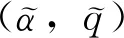
(34)

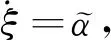
(35)

则(ξ,χ1,χ2)系统可表示为

(36)

至此，“直接导数耦合”转换为“间接导数耦合”，弱化了姿态系统的强耦合。

注3：这里采用的耦合弱化思想，在本质上并没有改变系统的状态方程，只是通过引入虚拟参数将原系统的“直接导数”抽离出来转换成了“间接导数”。通过分析可知，攻角/俯仰角速率耦合无法采用耦合消除策略[8-9,12-13，15]，因此对其引入了耦合弱化思想。

俯仰力矩控制指令选择为

mcmd=Iyy0[[-μ-κ5a1]χ2+

(37)

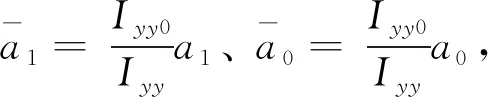
(38)

定义不确定参数矩阵θ3、矩阵ψ3及矩阵B3如下

ψ3=[-α3φ,-α2φ,-αφ,-φ,-α3,-α2,

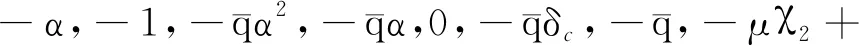
(39)

则(ξ,χ1,χ2)子系统可重写为

(40)

令ζ1=χ1、ζ2=χ2/κ5，则式(40)可转换为

(41)

其中，

(42)

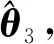
(43)

控制器设计为

(44)

对Lyapunov函数求导得

(45)

4 稳定性证明

定理1：考虑系统(1)、(2)，控制律选择为(12)、(21)、(44)，则系统输出信号y=[V,h]T可以渐进跟踪期望信号yref(t)=[Vref(t),Href(t)]T，即跟踪误差最终渐近稳定，闭环系统所有变量最终有界[16]。

证明：闭环系统Lyapunov函数选取为

(46)

对Z求导有

(47)

将式(13)、式(26)、式(45)代入到式(47)中，有

(48)

其中，

R(t)=

(49)

选择适当的参数κ1>0,μ>0,κ5>0，则R(t)正定。因此有

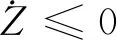
(50)

由式(50)可知，协调控制指令φ、γcmd(t)、αcmd(t)、qcmd(t)与协调控制器(12)、(21)、(44)可以保证被控系统(1)与(2)所有变量有界，因此纵向闭环系统最终一致有界。

5 仿真分析

将仿真初始条件设定为：H=30000m、V=3000m/s、φ=0、α=1°、γ=0°、q=0°。期望的指令为Href=30500m、Vref=3050m/s。在初始条件下，所有的气动参数具有30%的不确定性。控制器参数选择为：κ1=2,κ2=1,κ3=4,κ4=6,κ5=2,Γ1=0.1×I16×16,Γ2=0.1×I5×5,Γ3=0.1×I13×13,μ=0.75,a0=0.5,a1=1.5,Iyy0=85000。仿真图如图3所示。

(a) 速度跟踪曲线

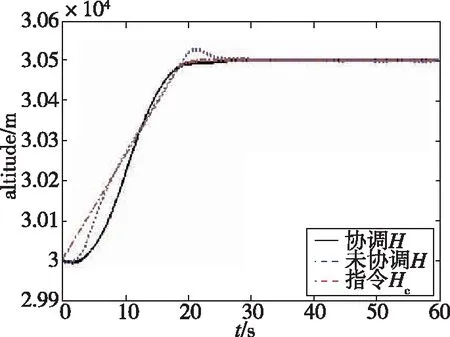
(b) 高度跟踪曲线

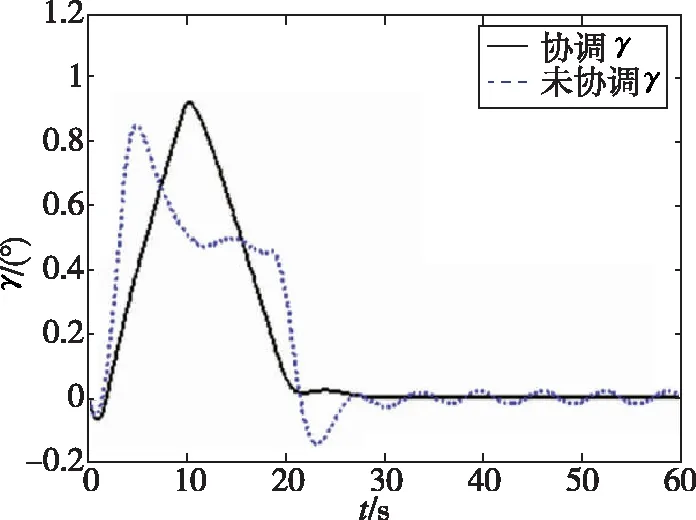
(c) 航迹角跟踪曲线

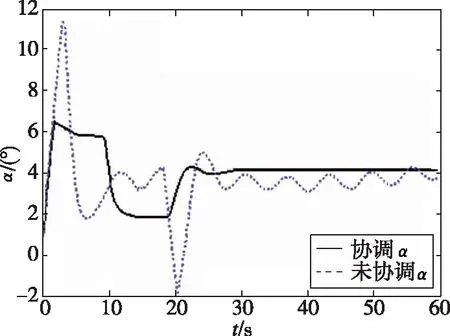
(d)攻角跟踪曲线

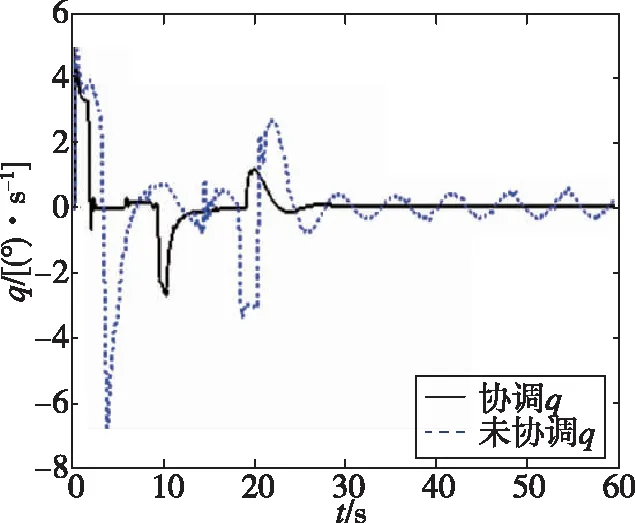
(e)俯仰角速率跟踪曲线

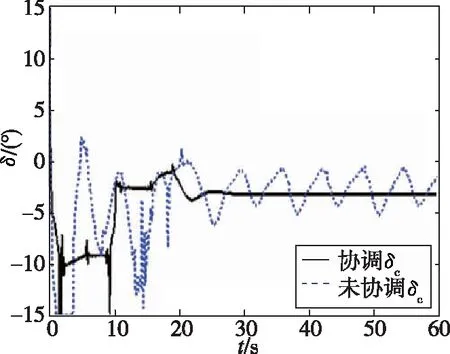
(f)鸭翼舵偏转曲线

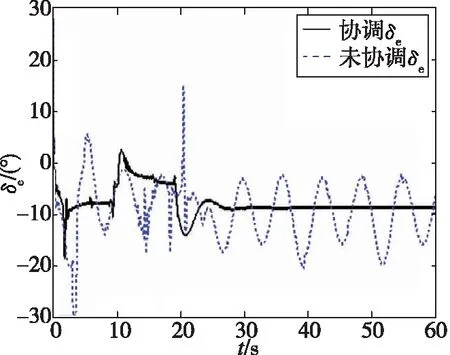
(g)升降舵偏转曲线

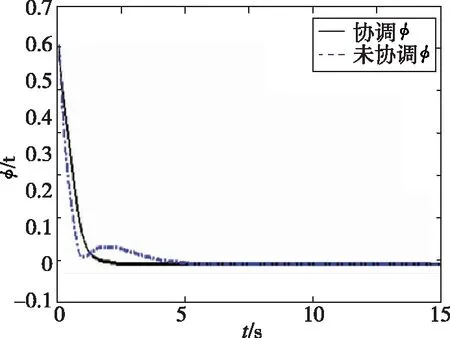
(h)油门开度当量比变化曲线图3 纵向系统仿真对比曲线Fig.3 The comparison results of longitu-dinal trajectory variables

由图3(a)可以看出，鲁棒协调控制器的性能明显优于一般控制器。在0s到10s过程中，速度通道在一般控制器作用下，有较大的振荡。在18s后进入稳态时，速度通道仍然有振荡。经对比发现，在鲁棒协调控制器的作用下，速度跟踪曲线的性能有所提升，跟踪过程没有出现明显的振荡，处理速度通道的不确定明显加强。由图3(b)可知，高度通道在一般控制器作用下，在0s到20s过程中，出现了2次振荡，在进入稳态后有较大超调。在对比鲁棒协调控制器后发现，高度通道指令跟踪速度变快，无振荡，动态性能提升。由图3(c)、图3(d)、图3(e)可知，在鲁棒协调控制器的作用下，跟踪曲线动态性能较好，调节次数减少，曲线更为平滑。由图3(f)、图3(g)可知，在鲁棒协调控制器作用下，舵面偏转效率较高，舵面振荡次数减少，振荡幅度减小，舵面调节次数减少。由图3(h)可知，在鲁棒协调控制器作用下，油门开度当量比变化曲线更为平滑，整个调节过程无振荡，无抖动，燃料燃烧后产生的推力比较平稳，利于飞行器的调节。在一般控制器作用下，油门开度当量比会出现振荡，燃料燃烧后产生的推力是频繁振荡的。这将不利于飞行器的调节，会对飞行器造成损伤。

6 结 论

本文针对高超声速飞行器纵向系统进行了耦合分析，并基于耦合补偿与转换技术设计了纵向系统鲁棒协调控制器。同时，针对纵向系统的不确定性，通过引入投影映射算法，将系统模型中的参数不确定项分解成了参数不确定矢量矩阵，利用自适应估计器在线实时估计了系统的不确定性。仿真比对分析结果表明，所设计的鲁棒协调控制器对系统的不确定性与耦合具有较强的鲁棒性与协调性，提高了系统的协调能力。