微分求积法求解梁的位移方程

吴 明 明

(河北工程大学土木工程学院，河北 邯郸 056038)

0 引言

功能梯度材料[1](FGM)是一类复合材料，其从一个表面到另一个表面具有连续的材料特性变化，因此消除了在层压复合材料中界面处的应力集中。通常，FGM由陶瓷和金属的混合物制成，陶瓷可以在热环境中抵抗高温，而金属可以降低在陶瓷表面上发生的拉应力。FGM广泛用于机械，航空航天，核能和土木工程。

微分求积法[2](Differential Quadrature Method，简称DQM)被认为是一种需求的离散点少而数值精度又较高的数值方法，它的基本思想是把解函数在给定离散点上的导数值用计算域内全部离散点处函数值的加权和近似地表示。以高阶剪切梁为例，介绍了DQM法在结构中的应用[3]，并着重讨论了DQM所得的数值解与精确解的一致性，体现了该方法实用性。

通过微分求积法进行数值求解。分析了不同的边界条件及节点数对梁弯曲的规律。

1 基本理论

如图1有长度L、宽度b和高度h的矩形横截面功能梯度梁。坐标x，y和z分别指向梁的长度、宽度和高度方向，如图1所示。根据线弹性假设，该功能梯度梁的位移场为：

(1)

其中，u为梁中面上某点的轴向位移;wb,ws分别为梁中面上某点的横向位移的弯曲和剪切分量;f(z)为形状函数，可确定横向剪切应变和剪切应力沿梁厚度的分布形式。非零应变由下式给出：

(2)

2 控制方程

根据虚功原理来推导控制方程。该理论形式可以表述为：

0=δU+δW

(3)

其中，δU为虚应变能；δW为虚功。梁的应变能的变化可以表示为：

(4)

由横向载荷q和弹性地基引起的虚功可以表示为：

(5)

将式(4)和式(5)中δU和δW代入等式(3)，并对空间变量进行积分，可得功能梯度梁的控制方程：

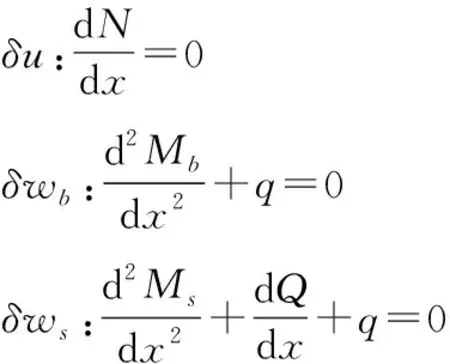
(6)

FGM梁的本构关系可以写成：

σx=Q11(z)εx
σxz=Q55(z)γxz

(7)

将式(2)代入式(7)，可得到力、力矩和剪力的合力的表达式：

(8)

将式(8)代入式(6)，控制方程可以用位移(u，wb，ws)表示为:

(9)

(10)

(11)

3 微分求积法的应用

微分求积法(DQM)的本质是将函数在求解区域内的全部节点处的导数值，近似地用其相应节点处的函数值的加权和来表示，也就是说我们可以把微分方程转化为一组用节点处的函数值作为未知量的代数方程组，进而求解该代数方程组，即可得微分方程的数值解。例如将控制方程式(9)进行DQM离散，可转化为代数方程组：

(12)

4 数值算例与讨论

选用金属和陶瓷合成的功能梯度材料，以验证现有理论在解决简支FGM梁的弯曲变形问题时的准确性。上部为铝和下部为氧化铝材料组成的FGM梁。铝的材料特性为Em=70 GPa，νm=0.3，氧化铝的材料特性为Ec=380 GPa，νc=0.3。为方便起见，使用以下无量纲形式：

(13)

4.1 不同节点个数时的弯曲结果比较

为了说明DQM法求解高阶剪切变形梁弯曲力学行为的有效性和准确性，取节点数为不同值时梁横向位移的数值解与精确解进行了比较，在两种L/h和不同梯度因子p变化时的横向位移如表1所示。可以看出与参考文献[4]中的结果非常接近，误差非常小，这说明该方法有很高的精度，是一种有效的数值方法。

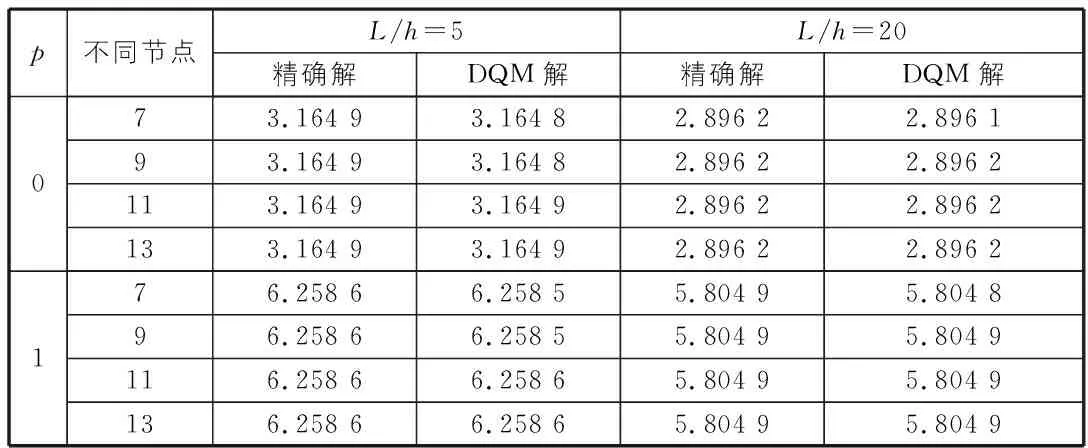
表1 不同节点数值下的横向位移变形对比

4.2 不同边界条件的弯曲结果分析

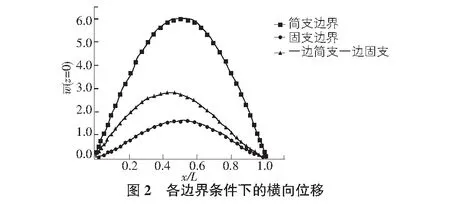
为了说明不同边界条件对均匀载荷下FGM梁弯曲变形的影响，我们给出了三种不同边界条件下梁的横向位移(见图2)。简支条件和固支条件下梁的位移呈对称分布，一端简支一端固支时梁的最大位移没有在梁的中心，表明通过DQM得到的数据很好的体现了梁的挠度变化规律。

5 结语

1)本文建立了各种高阶剪切变形梁理论，用于FGM梁的弯曲。用微分求积法求解了梁的弯曲问题的计算公式。

2)通过数值算例的分析比较体现了微分求积法具有较高的计算效率和计算精度，用了很少的节点得到较好的结果，是一种较好的计算方法。