多元函数取值范围问题的常见求解失误

广东省深圳市盐田高级中学 (518083)

罗 诚

在解答多元函数取值范围问题时，由于涉及多个变元，在解题过程中，相对于单变量函数取值范围问题，更容易出现这样或者那样的失误.有感于此，本文拟将解决这类问题时的常见失误进行梳理归类，以供教学参考.

一、疏漏显性题设

对于多元函数取值范围问题，关联多个变量，常常题设较多.在求解过程中，容易出现顾此失彼的情况，以至于疏漏显性题设导致解题失误.

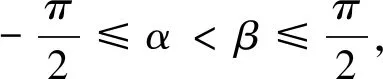
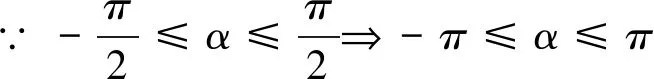
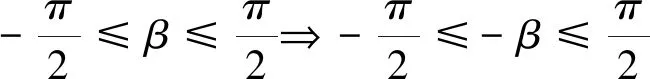
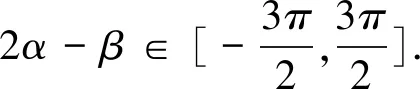
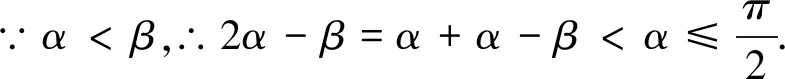
图1

+∞).

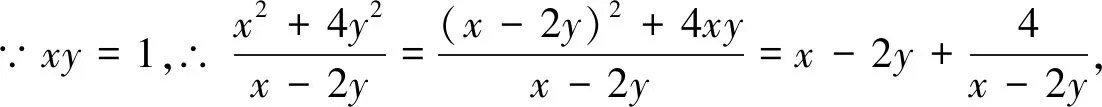
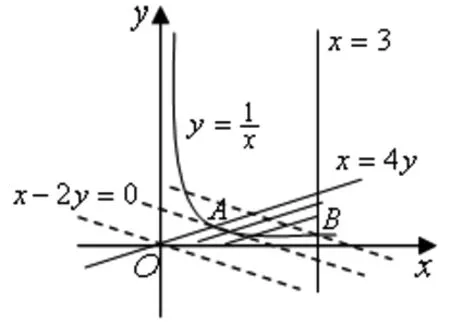
图2

二、忽视等号成立

等号能否成立，关乎到多元函数取值范围的上下确界.在解题过程中，倘若不慎，就有可能出现等号不成立的情况，从而由此出现解题失误.

例3 若正数x,y满足x+3y=5xy，求3x+4y的取值范围.

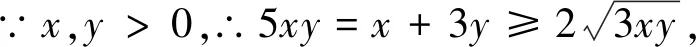
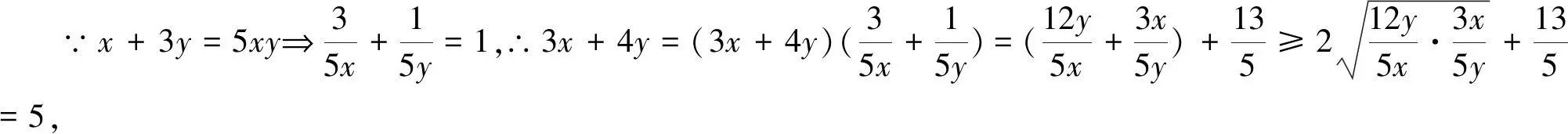
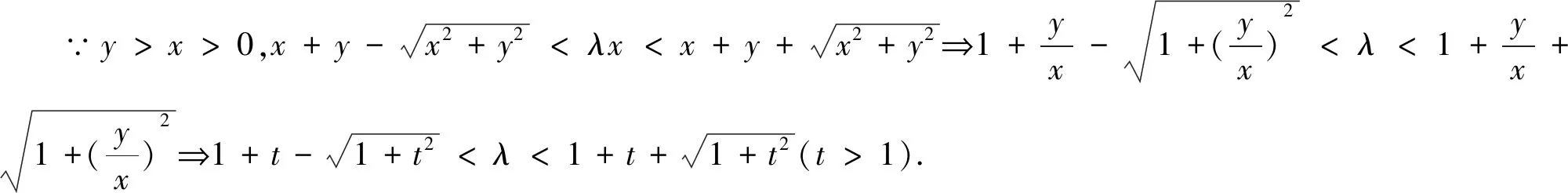
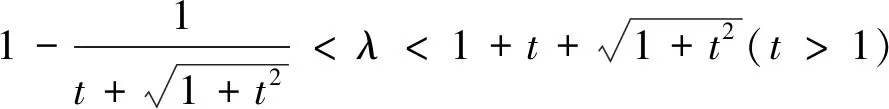
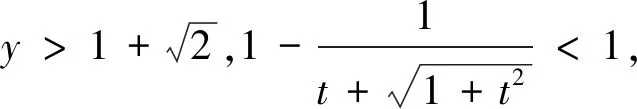
三、变更变元范围

求解多元函数取值范围问题，在变形的过程中，出现不等价变形，引起变更变元范围的失误是司空见惯的.

例5 已知实数x,y满足3x2+2y2=6x,求u=x2+3y2的取值范围.

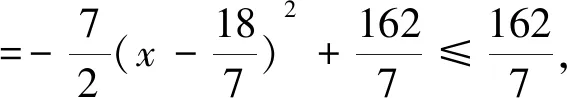
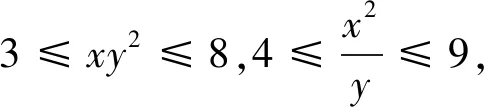
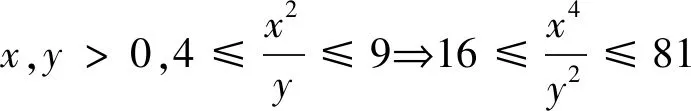
剖析:上述解法，变形过程扩大了变元x,y的取值范围，正确解法如下：

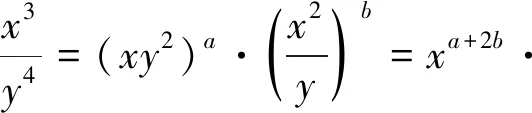
四、描绘图像失真

限于直观的局限，难免在描绘图像时，使描绘出的图像产生失真，并由此形成解题失误.

例7 在平面直角坐标系中，点A，B，C的坐标分别为(0，1)，(4，2)，(2，6)．如果P(x，y)是△ABC围成的区域(含边界)上的点，那么当u=xy取到最大值时，点P的坐标是．

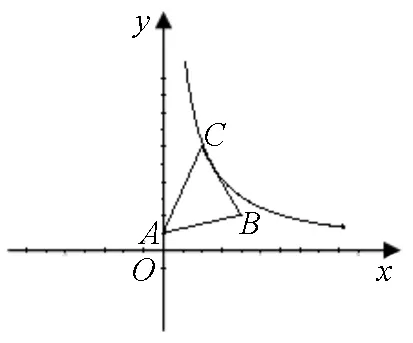
图3

误解:画出图形，如图3，联想到线性规划问题解法，由图形直观可知，当点P与点C(2,6)重合时，w=xy的最大值为12.

辨析:上述解法似乎无误，但这种解法是由于描绘图像失真的误解.

请看以下的定量分析：

由题意可得线段BC的方程为y=-2x+10(2≤x≤4)，代入u=xy可得u=x(-2x+10)=

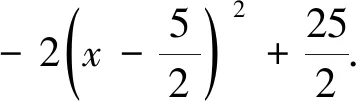
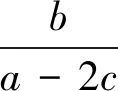
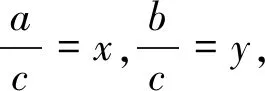
图4

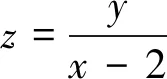
辨析:上面给出的是一种典型的图像失真导致的误解.

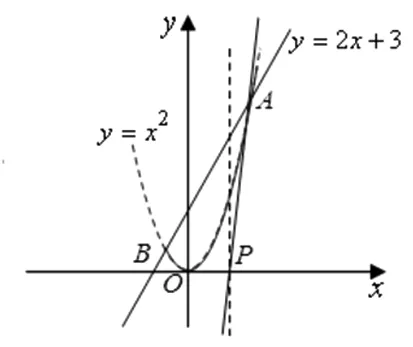
图5