看似无圆胜有圆 多解之中本质现

北京市陈经纶中学 (100020)

张留杰 孙丕训

解三角形问题是历届高考的热点之一，作为填空题的压轴题在高考模拟试题中倍受青睐，试题虽小，但思辨味儿浓、解法多样，内涵丰富．

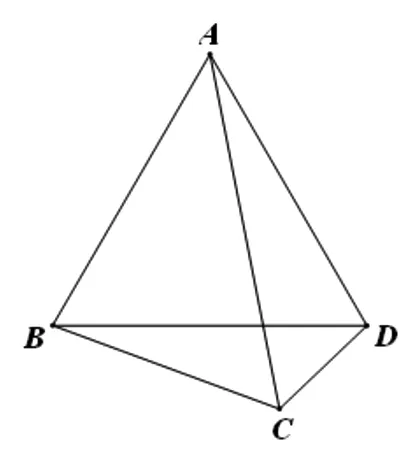
图1

题目(湖北省八校2018届高三第二次联考16)如图1，平面四边形ABCD中，△ABD为等边三角形，且BC=2，CD=1，则△ABC面积的最大值为．

一、解法剖析

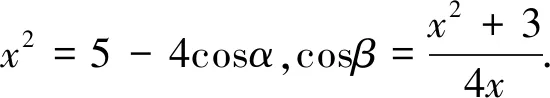
评注：由已知条件，先聚焦于△BCD，借助正、余弦定理分别表示正△ABD的边长和△ABC的面积，最终用关于角α的三角函数求出面积最大值，属通性通法．

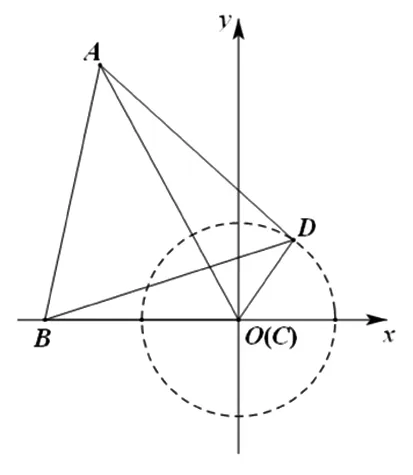
图2

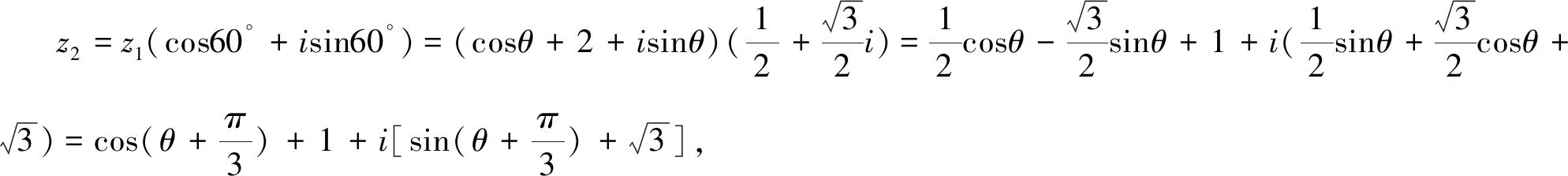
评注：解析法是用代数方法解决几何问题的主要手段，若固定线段BC，不难得出点D在单位圆上运动，由等边三角形想到向量的旋转，所以借助复数及其几何意义快捷得出△ABC面积的最大值，思路自然，过程简洁．

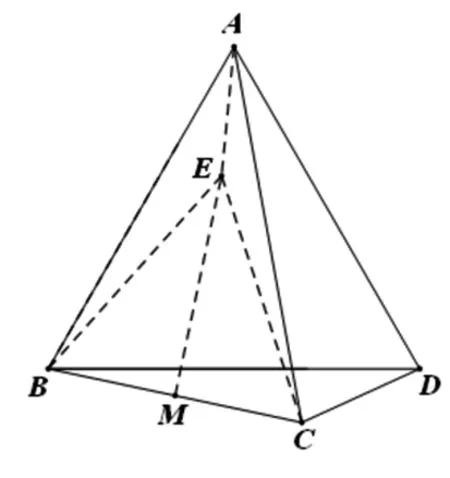
图3

解法三：如图3，将线段BC绕点B，按逆时针方向旋转60°至BE，连结EC、AE，易得△BCE为等边三角形，又等边△ABD，易证△BAE≅△BDC，所以AE=DC=1．

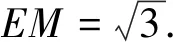
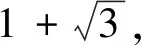
评注：题目条件中只有边长没有角度，利用等边三角形的中心对称性，旋转线段BC，构造另一等边三角形，则点A相对于正△BCE而言，总在以点E为圆心半径为1的圆上运动，由图形特征不难得出BC边上高线的最大值．方法巧妙，思维灵活，对直观想象能力要求较高．

二、问题的几何本质揭示

回顾以上解题过程，发现此问题的形成过程源起一对同心圆，经过一番探究，我们得出问题的一般模型，揭示了试题的几何本质．

结论B、D是半径分别为a、b(a>b)的同心圆C上的两动点，CB=a，CD=b，以BD为边作等边△BDA，则

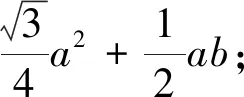
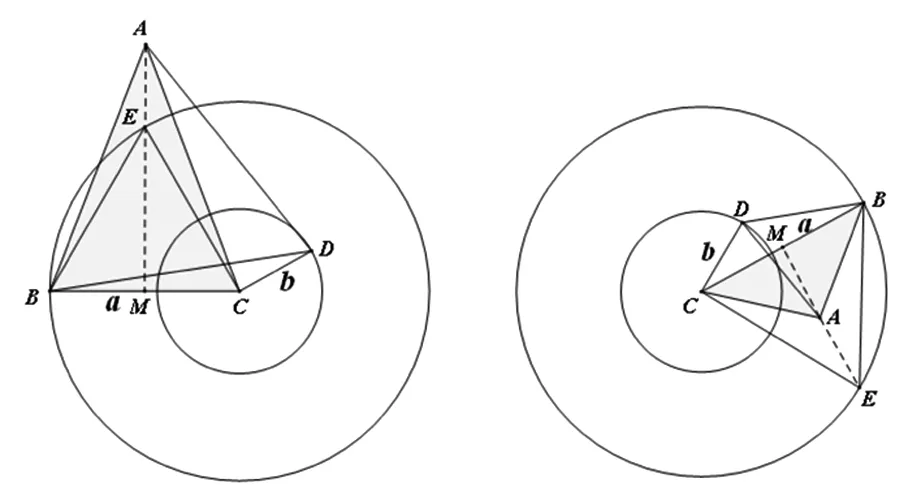
图4 图5

(2)线段AC的最大值为a+b；最小值为a-b(如图6、7)．

类比上述解法三，以上结论不难证明(这里从略)．

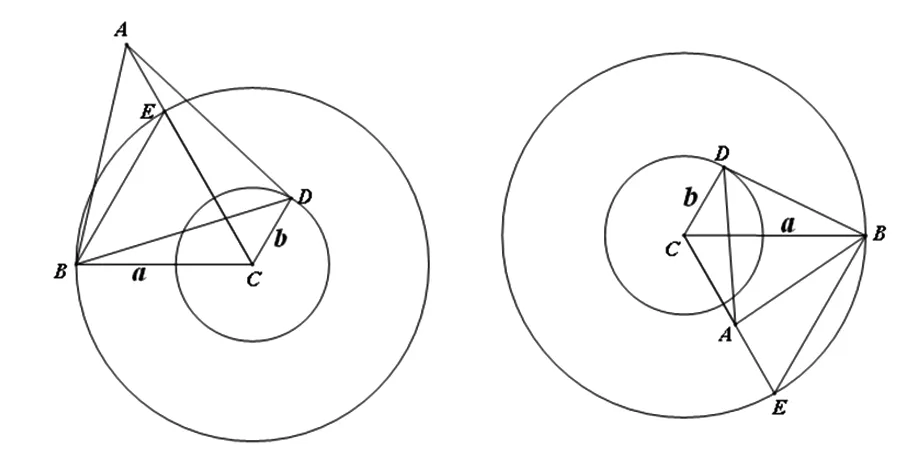
图6 图7