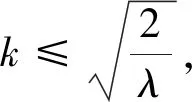对IMO42-2加强推广的三个另证

浙江省杭州市长河高级中学 (310000) 浙江大学附属中学丁兰校区 (310021)

夏伟峰 施刚良

文[1]、[2]、[3]作者都对于下列猜想：

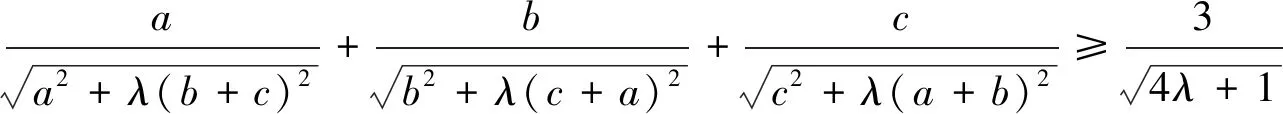
受文[1]、[3]、[4]的启发，下面笔者给出第一个另证：

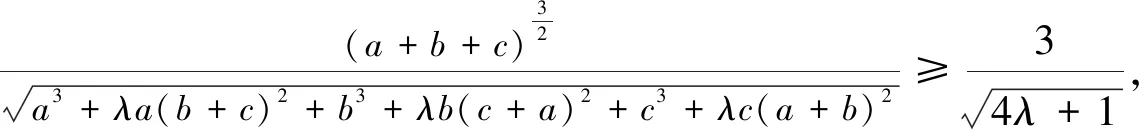
下面令f(λ)=(4λ+1)(a+b+c)3-9[a3+λa(b+c)2+b3+λb(c+a)2+c3+λc(a+b)2]，则f′(λ)=4(a+b+c)3-9[a(b+c)2+

b(c+a)2+c(a+b)2]=3a(b2+c2)+3b(c2+a2)+3c(a2+b2)+4(a3+b3+c3)-30abc≥3a·2bc+3b·2ca+3c·2ab+4·3abc-30abc=0.于是f(λ)在[2,+∞)上是单调递增，而f(2)=9{(a+b+c)3-[a3+2a(b+c)2+b3+2b(c+a)2+c3+2c(a+b)2]}=9[a(b2+c2)+b(c2+a2)+c(a2+b2)-6abc]≥9(a·2bc+b·2ca+c·2ab-6abc)=0.所以f(λ)≥f(2)=0.到此就证明了(*)，从而猜想成立.

评注：文[1]作者利用权方和不等式和柯西不等式将猜想不等式得以放缩，最后用一个巧妙的因式分解将猜想不等式加以证明，但这个分解不太容易想到.笔者通过权方和不等式将证明的任务落实到证明不等式(*)成立上，最后通过构造关于λ的一次函数，利用单调性解决，思维过程简单自然.

受文[5]的启发，下面笔者给出第二个另证：

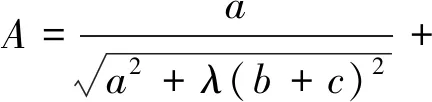
B=a(a2+λ(b+c)2)+b(b2+λ(c+a)2)+c(c2+λ(a+b)2).

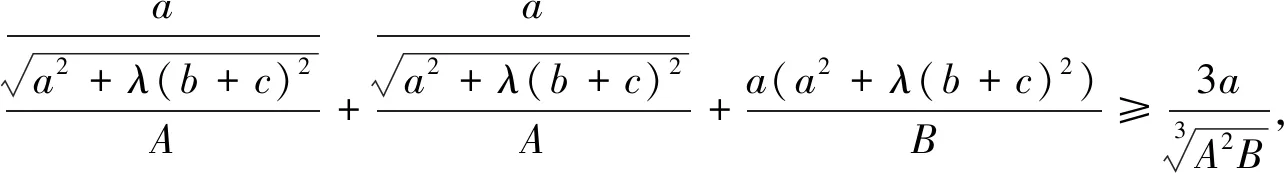
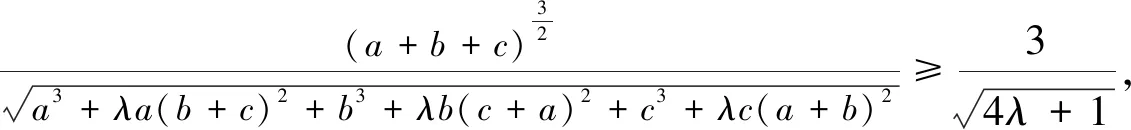
越南不等式专家范建熊所说：Jensen不等式(凹凸函数)很少用，是因为人们一直认为它对困难的问题力不从心.然而，这是个不等式未开垦的领域，Jensen不等式(凹凸函数)会变得非常有效，能够经常给我们带来意想不到的解决方案.

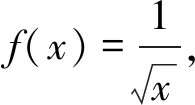
当λ≥2时，(4λ-8)∑a3≥(4λ-8)(∑a(b2+c2)-3abc)，所以(4λ-8)∑a3+(3λ+3)∑a(b2+c2)+(6-30λ)abc≥(4λ-8)(∑a(b2+c2)-3abc)+(3λ+3)∑a(b2+c2)+(6-30λ)abc=(7λ-5)∑a(b2+c2)+(30-42λ)abc≥(7λ-5)·6abc+(30-42λ)abc=0.

评注：文[3]作者通过两次柯西不等式将猜想不等式加以放缩，证明过程略显繁琐.本文通过函数的凹凸性将不等式放缩，落实到证明不等式(**).(**)的证明过程用到常用不等式∑a3+3abc≥∑a(b2+c2).从上面的证明中我们还发现，猜想不等式为什么要加λ≥2这个条件，不然这个不等式不一定成立，由此可以得到要使不等式成立，λ≥2是最优条件.

著名数学家波利亚说过：没有任何一个题目是彻底完成了的，总还会有些事情可以做；在经过充分的研究和观察以后，我们可以将任何解题方法加以改进；而且无论如何，我们总可以深化我们对答案的理解.笔者提出如下猜想：

若a,b,c∈R+，是否存在正数λ,k，使得

受文[4]、[5]的启发，笔者通过构造一组不等式和利用待定系数法，开始如下探究过程.

下面构造下列不等式组：

其中参数t待定.

所以，0<λ≤2时，k≤1，得到