以“不变应万变”突破“水银移动”类型教学难点
广东
高中物理选修3-3部分的气体实验定律在《考试大纲》中的要求属于Ⅱ级要求,为较高的要求,从近年全国各地高考的物理命题来看,气体实验定律的考查作为一道计算题形式年年必考。而将气体实验定律与液柱移动问题有机结合起来命题,一直都受到高考命题人的青睐。这类问题一般要经过分析、推理,然后判断得出结论,能够较好地考查学生分析推理能力,应用数学方法解决物理问题的能力。
水银在玻璃管内移动为动态过程,特别是在U形管内的移动,一边下降,另一边上升,涉及复杂的数学几何关系。在教学过程中,笔者感觉学生遇到此类问题时总是一片茫然,无从下手,常常把相应的几何关系弄错,导致全盘皆输。对于此类问题,采用假定水银不动,以“不变应万变”,使得这个教学难点得到有效突破,从而有“豁然开朗”“柳暗花明又一村”的感觉。
一、假定液柱不动,速断移动方向
在解决热学问题中常常会遇到温度发生变化时,判断被水银柱隔开的两部分气体移动方向的问题。水银柱移动方向的关键在于两侧气体压强的变化大小,由此我们可以假定液柱静止不动,通过研究两侧气体的状态变化来进行判断。

图1
【例1】如图1所示,两端封闭、粗细均匀、竖直放置的玻璃管内,有一长为h的水银柱将管内气体分为两部分,其中上部分体积大于下部分体积,水银处于静止状态。使两部分气体同时升高相同的温度,管内水银柱将如何运动?(设原来上、下两部分气体温度相同)
【解析】水银柱原来处于静止状态,故其所受合力为零,设上部分的压强为p1,下部分气体的压强为p2,由题意可知,p2=p1+ph。温度升高后,若水银静止不动,两部分气体的压强都增大,若Δp1=Δp2,两部分气体增加的压强相等,水银柱不动;若Δp1>Δp2,上面气体增加的压强大,水银柱所受合外力方向向下,应向下移动,若Δp1<Δp2,上面气体增加的压强小,水银柱向上移动。所以判断水银柱怎样移动,就是分析其合外力的方向,即判断两部分气体的压强哪一个增大得多。

【例2】两端封闭、内径均匀的直玻璃管水平放置,如图2所示。右边气体的体积大于左边气体的体积,即V右>V左,温度均为20℃,现将左端空气柱的温度降为10℃,右端空气柱的温度降为0℃,则管中水银柱将
( )

图2
A.不动
B.向左移动
C.向右移动
D.无法确定是否移动
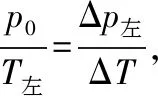
二、假定水银不动,妙算几何关系
在气体实验定律的应用中,有一类题型是由于温度变化或外加水银,导致气体的体积、压强发生变化,进而使得水银发生移动,从而产生复杂的几何关系变化,要弄清这些水银之间的几何关系,采用“假定水银不动”来进行求解,往往起到事半功倍的效果。
【例3】如图3所示,粗细均匀一端封闭一端开口的U形玻璃管竖直放置,水银将管内一定质量的理想气体封闭在U形管内,当t1=31℃,大气压强p0=76 cmHg时,两管水银面相平,此时左管被封闭的气柱长L1=8 cm,则当温度t2是多少时,左管气柱L2为9 cm?

图3
【解析】由题意可知,L2为9 cm,可见左边下降1 cm,右边升高1 cm,这样两边水银高度差应该为2 cm,整个过程水银是“移动”的,处于变化的过程。不妨设整个过程中水银一直处于静止,直接等效把左边1 cm水银柱“搬到”右边,如图4所示。设玻璃管的横截面积为S。则有
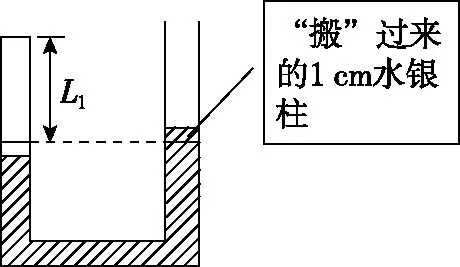
图4
初状态,p1=p0=76 cmHg,V1=L1S=8S,T1=(273+31) K=304 K;
末状态,p2=p0+Δh=(76+2) cmHg=78 cmHg,V2=L2S=9S,T2=273+t2

解得t2=78℃

图5
【例4】如图5所示,左端封闭、右端开口且粗细均匀的U形管竖直放置,管内用水银将一段气体封闭在管中。当温度为280 K时,被封闭的气柱长L=22 cm,两边水银柱高度差h=16 cm,大气压强p0=76 cmHg。求:
(1)为使左端水银面下降3 cm,封闭气体温度应变为多少?
(2)封闭气体的温度重新回到280 K后,为使封闭气柱长度变为20 cm,需向开口端注入的水银长度为多少?


图6
(2)封闭气体的温度重新回到280 K,相当于气体又回到初始状态,如图5所示,为使封闭气柱长度变为20 cm,由题意可知,在右边加入一定高度的水银,整个水银是移动的,即左边水银升高2 cm,右边水银下降,整个过程水银高度的变化是复杂的,不易求出两液面的高度差。如果“假定水银不动”,则整个变化可等效为左边封闭气体“注入”2 cm高的水银,右边注入x(单位:cm)的水银,如图7所示。这样以“不变应万变”,很容易求出两液面高度差为Δh2=h+2-x=18-x。所以此时封闭气体的压强为p3=76-Δh2=58+x,其体积为V3=(22-20)S=20S,对左边气体由状态1(图5)到状态3(图7)变化过程中其温度不变,由玻意耳定律有p1V1=p3V3,即60×22S=(58+x)×20S,解得x=8 cm,即需向开口端注入的水银柱长度为x+2 cm=10 cm。

图7

