接触物体的“分离”问题归类探讨

河北

在相互接触物体的系统中，由于外力作用或运动状态发生变化，导致两个物体之间的相互作用力发生变化，在一定条件下会发生分离。因问题环境错综复杂，分离点的确定通常是解决此类问题中的关键点和难点，这就需要在相应的环境下进行分析推理，抓住分离时相互作用力为零，以及对应接触物体的速度、加速度等特点，使问题得以解决。这类问题经常出现在高考中，很多学生由于不能快速找到解决问题的关键而失分，本文旨在对高中常遇到的这些问题进行归类探析，希望能对读者有所帮助。

1.加速度变化时物体与接触面分离

物体或系统的运动状态发生变化时，物体间的弹力大小也随之变化，当加速度满足一定条件时，可能会出现物体与接触面分离。

【例1】如图1所示，光滑水平面上，在倾角为45°光滑斜面体的顶端P处固定细线的一端，细线的另一端拴一质量为m的小球，现对斜面体施加逐渐增大的水平外力，使斜面体与小球一起向左加速运动，求：

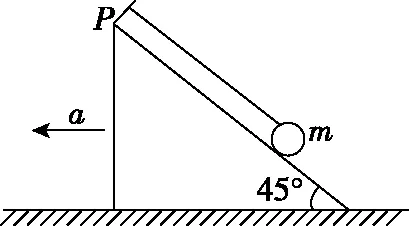
图1

(1)当斜面体至少以多大的加速度向左运动时，小球对斜面的压力为零；

(2)当斜面体以a=2g的加速度向左运动时，细线的拉力为多大。

【分析】设小球在斜面上随斜面一起加速时，受力分析如图2所示，受到的拉力为FT，斜面对小球的支持力为FN。

水平方向满足FTsin45°-FNcos45°=ma

竖直方向满足FTcos45°+FNsin45°=mg

随着加速度的增大，综合以上两式可以看出拉力FT逐渐增大，支持力FN将逐渐减小，减小为0后再增大加速度，小球将由斜面上离开。

图2

图3

【解析】(1)当小球对斜面压力为零时，对小球受力分析如图3所示。

竖直方向FTcos45°=mg

水平方向FTsin45°=ma

联立得a=g

图4

(2)当斜面体以a=2g>g的加速度向左运动时，小球会“飘”起来，对小球受力分析如图4,假设FT与竖直方向夹角为θ。

竖直方向FTcosθ=mg

水平方向FTsinθ=ma

【例2】如图5所示，半径为R的光滑圆柱体恰好放在一个木质的圆弧槽内，球心为O，它们的左边接触点为A，槽半径略大于R，且OA与水平面成α角。圆柱体的质量为m，木质槽的质量为M，木质槽处于光滑水平面上。现给木质槽一水平向右的拉力F，要使圆柱体和木质槽一起加速运动且保持相对静止，拉力F大小需满足什么条件。

图5

【分析】当F增大到一定值时，圆柱体将从槽中飞出，关键是得出此时对应的受力条件。

【解析】对系统整体分析可知F=(m+M)a。

当加速度达到一定值时到达临界状态，此时圆柱体对圆弧的底部压力为0，只受重力和点A的支持力，加速度再增大球可能从槽内飞出，受力分析如图6所示。

图6

竖直方向满足FNsinα=mg

水平方向满足FNcosα=ma

【反思】在以上两个问题中，球与斜面或槽的底面压力随着系统的加速度增大，压力会逐渐减小，球与斜面或圆柱体与圆弧槽会出现分离情形，解决问题的关键是落实分离时对应的临界条件。

2.弹簧作用下两个物体分离

相互接触的两个物体，在弹簧作用下一起运动的过程中，相互作用力也会随位置的变化而变化，在一定条件下也可能分离，但分离的位置需要视具体情况确定。

【例3】如图7所示，O为弹簧的原长位置，物块A、B是紧靠在一起的两个物体，物体B与弹簧相连接，当用外力将弹簧压缩至一定程度后放手，物体A、B在弹力的作用下向左运动，一段时间后两个物体分开，两物体均可视为质点，两物体与地面间的动摩擦因数分别为μA和μB，则关于两物体运动过程中分离的位置，以下说法正确的是

( )

图7

A.若水平面光滑，A、B一定在O点分离

B.如果μA等于μB，两物体在O点右侧分离

C.如果μA大于μB，两物体在O点左侧分离

D.如果μA小于μB，两物体的分离点在O点的左侧

【反思】两物体一起做变加速直线运动，过程中相互作用力逐渐减小，当相互作用的弹力FN等于零时；两物体出现分离，此时两物体瞬时加速度相等，不能简单地认为两物体在弹簧原长时分离。

3.外力和弹簧共同作用下匀加速直线运动情况下的分离

系统在弹簧弹力及外力共同作用下做匀加速运动，由于弹簧弹力不断变化，导致系统内物体间的相互作用力逐渐变化，在一定条件下也会出现分离现象。

图8

【例4】如图8所示，一个弹簧台秤的秤盘质量和弹簧质量都不计，盘内放置一个物体P处于静止状态，P的质量m=10 kg，弹簧的劲度系数k=250 N/m。现在给P施加一个竖直向上的力F，使P从静止开始向上做匀加速直线运动，已知在t=0.2 s内F是变力，在0.2 s后F是恒力，g=10 m/s2，则F的最小值和最大值分别是

( )

A.240 N，360 N B.250 N，350 N

C.50 N，150 N D.200 N，300 N

【反思】在这个问题中，盘的质量不计，一直处于平衡状态，物体与盘分离即与弹簧分离，根据弹力的作用特点，可知分离时弹力为0，确定分离时的相关方程，可知弹簧在原长分离。

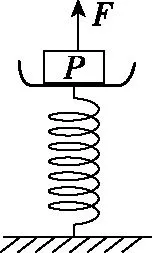
图9

【例5】如图9所示，一个弹簧台秤的秤盘质量为1.5 kg，弹簧质量不计，盘内放置一个物体P处于静止状态，P的质量为10.5 kg，弹簧的劲度系数k=800 N/m。现给P施加一个竖直向上的力F，使P从静止开始向上做匀加速运动。已知在前0.2 s内F是变化的，在0.2 s后F是恒力，g=10 m/s2，求：

(1)未施加力F时，弹簧的压缩量；

(2)物体做匀加速直线运动的加速度大小；

(3)F的最小值与最大值分别是多少？

【解析】(1)设P的质量为m，盘的质量为M，未施加拉力时，由平衡条件和胡克定律得

(M+m)g=kx1代入数据得x1=0.15 m

(2)物体与盘一起运动时对整体受力分析知

F+kx-(M+m)g=(M+m)a

对盘由牛顿第二定律得kx-FN-Mg=Ma

向上运动过程中，加速度恒定不变，弹簧的形变量x减小，弹力减小，相互作用力FN也会逐渐减小，当相互作用力减小为零时，两物体出现分离kx2-Mg=Ma

联立可解得a=6 m/s2

(3)刚开始作用时力F最小

Fmin+kx1-(M+m)g=(M+m)a

代入数据得Fmin=72 N

物体离开盘后拉力F最大Fmax-mg=ma

代入数据得Fmax=168 N

【反思】此题易错点在于把握不住分离条件，错误地认为P与盘分离时，盘受力平衡，即Mg-kx=0。本题对物理过程的分析能力要求较高，通过对此物理过程的分析后，列出秤盘运动过程中的动力学方程，确定两物体分离的临界点。当弹簧作用下的两物体加速度、速度相同且相互作用的弹力FN=0时，恰好分离，注意由于此时物体具有向上的加速度，弹簧弹力大于秤盘质量，因而弹簧所处的位置不是原长。

4.物体在圆周轨道上运动过程中脱离

物体沿圆轨道做圆周运动时，当速度以及在轨道上的位置发生变化时，物体与轨道间的压力也会发生变化，在一定条件下会出现物体脱离轨道的情形。

【例6】如图10所示，一半径为R的光滑半球面固定在水平地面上，小物块A由顶端无初速度滑下，以下有关物块运动说法正确的是

( )

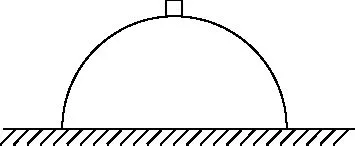
图10

A.物块将沿弧面一直运动到地面

B.物块在运动至圆弧面上某个位置时与弧面分离

D.物块整个运动过程中加速度大小可能不变

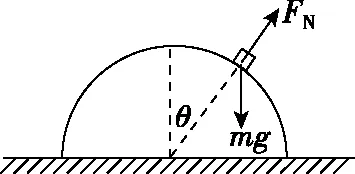
图11

( )

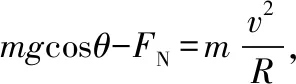
图12

A.若hA=hB=2R，则两小球都能沿轨道运动到最高点

C.适当调整hA和hB，均可使两小球从轨道最高点飞出后，恰好落在轨道右端口处

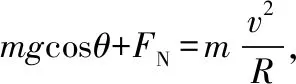
【反思】物体在圆周轨道上运动时，做的是圆周运动，随着速度的变化物体与轨道间的相互作用力也不断变化，当与轨道间压力减小到0时，将脱离轨道做抛体运动，但要注意分离时物体的速度不为零。

5.系统内物体在弹簧拉力作用下脱离接触面或两物体分离

在一些多物体关联的系统中，由于重力、电场力等约束条件物体静止于地面上或墙面上，系统内部由弹簧连接，在一定条件下，系统内部在弹力与外力作用下使物体之间或物体与地面、墙面分离，理解并熟练应用分离条件便会轻松解决问题。

【例8】如图13所示，挡板P固定在足够高的水平桌面上，小物块A和B大小可忽略，它们分别带有+QA和+QB的电荷量，质量分别为mA和mB。两物块由绝缘的轻弹簧相连，一不可伸长的轻绳跨过滑轮，一端与B连接，另一端连接一轻质小钩。整个装置处于场强为E、方向水平向左的匀强电场中。A、B开始时静止，已知弹簧的劲度系数为k，不计一切摩擦及A、B间的库仑力，A、B所带电荷量保持不变，B不会碰到滑轮。求：

(1)若在小钩上挂一质量为M的物块C并由静止释放，可使物块A恰好能离开挡板P，求物块C下落的最大距离；

(2)若C的质量改为2M，则当A刚离开挡板P时，B的速度多大。

图13

故C下落的最大距离为h=x1+x2

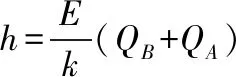
(2)由能量守恒定律可知C下落h过程中，C重力势能的减少量等于B电势能的增量、弹簧弹性势能的增量、系统动能的增量之和。

当C的质量为M时Mgh=QBE·h+ΔE弹

当C的质量为2M时

6.系统内物体在相对运动中分离

【例9】如图14所示，在光滑水平面上有一表面光滑、质量为M的立方体物块，一长度为l的轻杆下端与固定在地面上的光滑铰链连接于O点，可在图中竖直面内自由转动，杆的另一端连接着一个质量为m的小球，小球靠在立方体的左侧，开始时杆与水平方向成α角，立方体右侧受到水平向左推力F的作用，整个系统处于静止状态，若现在撤去水平推力F，则下列说法中正确的是

( )

图14

A.小球在落地瞬间和立方体分离

C.小球和立方体分离时刻的速度相等

D.小球和立方体分离时刻小球的加速度为g

【分析】撤去外力F后，小球将以O为圆心下落，同时推动立方体物块加速向右运动，落地时速度竖直向下，下落的整个过程中小球水平方向的速度先增大后减小，而物块在水平方向上只能加速而不能减速，因而小球在下落过程中会与物块分离。

【反思】巧妙利用分离时的关键条件，“相互作用力为0”，对有相对运动的系统采用隔离法与整体法综合分析，便可将复杂的问题迎刃而解。