解决多过程动力学问题的法宝——速度—时间图象的应用

贵州

一、基础知识

1.以横轴表示时间，纵轴表示速度，作出速度随时间变化的关系图，简称v-t图。匀变速直线运动的v-t图是一条倾斜直线，匀速直线运动的v-t图是平行时间轴的一条直线。

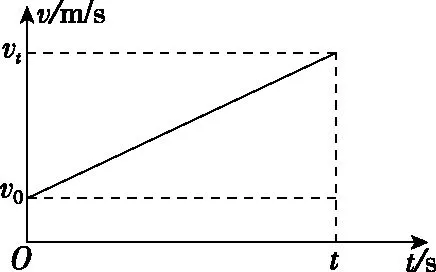
2.在v-t图中可以知道描述匀变速直线运动的五个物理量，即横轴看时间，纵轴看初、末速度，斜率看加速度，面积看位移。还有另外三个拓展物理量，一是中间时刻速度等于平均速度的同时也等于初末速度之和的一半，二是斜率与时间的乘积表示速度的变化量，三是斜率与质量的乘积表示物体所受的合力。

二、作图的步骤与技巧

1.首先建立横、纵坐标，标上符号和单位，长、宽比例适中，总体构成一个矩形；

2.确定第一个坐标点，如(0、v0)即零时刻时初速度不为零；

3.确定图的走向，在纵轴的正半轴斜向上表示增加，斜向下表示减少，在纵轴的负半轴斜向上表示减少，斜向下表示增加，同时要兼顾时间间隔；

4.确定拐点速度，同时兼顾拐点时刻，注意末速度和末时刻；

5.充分理解加速度的意义是每秒速度的变化量，利用速度公式的变式算出速度变化量、时间间隔、加速度之间的关系；

中午，营业部关门了，公安局的老邓挺着大肚子，背着双手，像只打鸣的公鸡一样踱到营业部，只要细看，他那黑浸浸的脸上明显地掩饰着幸灾乐祸。跟在他身后的小李斜跨着一绿色的挎包，一身公安制服穿得整整洁洁，平常乱糟糟的头发，今天从中间分成两瓣，像两片瓦一样搭在两只精神焕发的眼睛上，那发梢还挂着水，在阳光下闪闪发亮。

6.最后分析图象的意义，即横轴看时间，纵轴看初、末速度，斜率看加速度，面积看位移，面积差等于相对位移。

三、基础实践

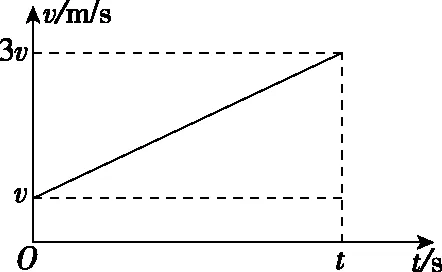
【例1】(2016年全国卷Ⅲ)一质点做速度逐渐增大的匀加速直线运动，在时间间隔t内位移为s，动能变为原来的9倍。该质点的加速度为

( )

【分析】根据题意末速度是初速度的三倍，经历时间t，位移为s，作出v-t图：

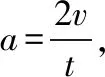
【例2】(2018年全国卷Ⅱ)汽车A在水平冰雪路面上行驶。驾驶员发现其正前方停有汽车B，立即采取制动措施，但仍然撞上了汽车B。两车碰撞时和两车都完全停止后的位置如图所示，碰撞后B车向前滑动了4.5 m，A车向前滑动了2.0 m，已知A和B的质量分别为2.0×103kg和1.5×103kg，两车与该冰雪路面间的动摩擦因数均为0.10，两车碰撞时间极短，在碰撞后车轮均没有滚动，重力加速度大小g=10 m/s2。求：

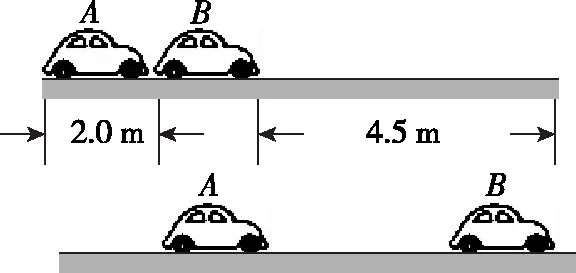
(1)碰撞后的瞬间B车速度的大小；

(2)碰撞前的瞬间A车速度的大小。

【分析】第一小问，设碰撞后瞬间B车速度的大小为v，做加速度大小为1的匀减速直线运动直到停止，根据题意作出v-t图：

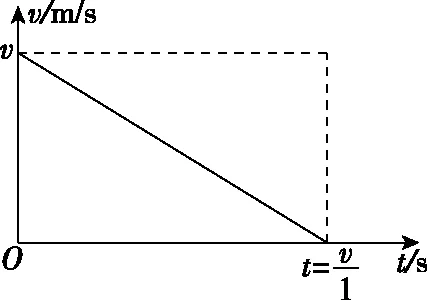
此图的难点是横轴时刻的大小等于初速度与加速度大小的比值，根据图象面积的大小等于位移的大小很快计算出v=3 m/s。

四、升华突破

【例3】长为1.5 m的长木板B静止放在水平冰面上，小物块A以某一初速度从木板B的左端冲上长木板B，直到A、B的速度达到共速0.4 m/s，然后A、B又一起在水平冰面上滑行了8.0 cm。若小物块A可视为质点，它与长木板B的质量相同，A、B间的动摩擦因数μ1=0.25。(取g=10 m/s2)求：

(1)木板与冰面的动摩擦因数；

(2)小物块相对于长木板滑行的距离。

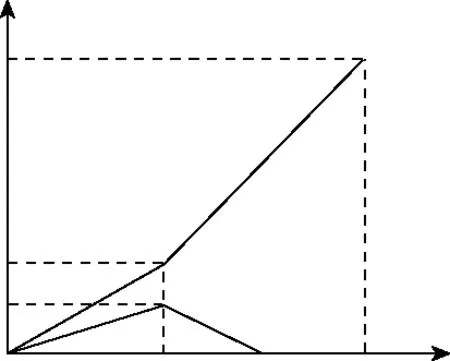
【分析】根据题目可得，A做减速运动，B做加速运动，AB共速后一起减速到停止。此题的难点是A在B的上面减速，最后一起在地面上减速，说明AB之间的摩擦因数大于B与地面的摩擦因数，加速度是摩擦力产生的，故A减速的图象要比AB一起在地面上减速的图象要陡一些。根据作图的步骤与技巧，作出v-t图：

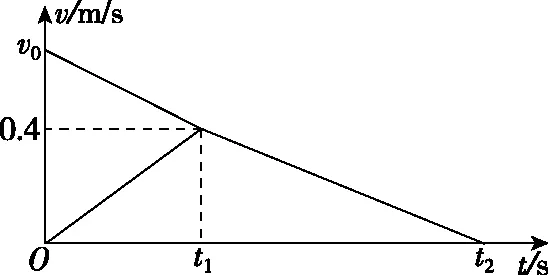
【分析】(1)后面三角形的面积在数值上等于AB一起在地面上滑行的位移大小，即8.0 cm，知道初、末速度和位移，可以算出加速度的大小是a=1.0 m/s2，因为加速度是摩擦力产生的，则摩擦因数是0.1。

(2)0.4 m/s是两个物体的共同速度，即图象中的拐点速度，A做减速运动，根据速度公式有0.4=v0-2.5t1，B做加速运动，是两个摩擦力共同作用产生的加速度，根据速度公式有0.4=0.5t1，上述两个方程可以得出v0=2.4 m/s，t1=0.8 s。

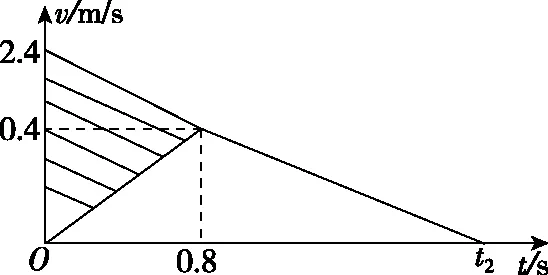
斜线部分三角形面积即A相对于木板B的位移，大小等于0.96 m。

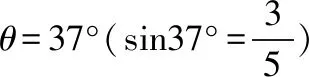
(1)在0～2 s时间内A和B加速度的大小；

(2)A在B上总的运动时间。

【分析】根据题意，A做两次加速度不同的加速运动，B先加速再减速最后静止，作出v-t图如图所示