基于区间直觉模糊数的旅游项目群决策方法研究*
潘芬萍,龚日朝
(湖南科技大学 商学院,湖南 湘潭 411201)
改革开放以来,我国实现了从旅游短缺型国家到旅游大国的历史性跨越,旅游业全面融入国家战略体系,成为国民经济战略支柱产业。原国家旅游局《2016中国旅游投资报告》显示,2016年我国旅游业投资达到12 997亿元,2017年预计超过1.5万亿元[1]。然而,在旅游业高速发展及大规模旅游投资热潮背后,存在着高成本低回报、投资回收期长、综合带动性差等诸多问题,旅游项目开发决策重要性凸显。
旅游项目决策是指项目开发前,通过构建科学合理的决策评价指标体系和评价准则,建立科学的数学模型和管理方法,对项目的开发条件、预期效益等作出客观、公正和准确的评价,从众多计划项目中选择最优项目进行开发的决策行为。很多学者从不同的视角构建了不同的旅游项目决策模型,如:线性规划模型[2]、结构方程模型[3]、概率模型[4]、资产资本定价模型[5]、AHP模型[6]、博弈模型[7]等。但我们分析发现,这些决策模型难以有效地利用一些非常重要的模糊评价指标,并将决策者的经验、偏好及其认知的模糊性纳入决策体系,不适合实践中集体群决策过程。事实上,旅游项目开发不仅具有很多未知的、不确定的条件因素,而且受到决策者思维的偏好及其认知模糊性的影响,往往导致一些非常重要的决策指标难以定量精确刻画,只能采取定性的模糊语言描述,因此,其属于多属性模糊群决策问题。
对于多属性模糊决策问题,学术界一直在不断探索其基本理论基础与决策方法体系。Zadeh[8]提出了模糊集概念,Atanassov[9]提出了直觉模糊集,并在1989年与Gargov 对其拓展,提出了区间直觉模糊集概念[10],还在1994年定义了其基本运算法则[11]。这些概念的提出,使得对事物属性的描述更为全面,对事物表现的能力也更突出。徐泽水[12]针对多属性决策问题,在直觉模糊数几何算子,如加权几何算子(IFWG)、有序加权几何算子(IFOWG)、混合几何算子(IFHG)等的基础上,提出了区间直觉模糊数的加权几何集成算子(IIFWGA)、加权聚集算子(IIFWAA)等;同时提出了通过区间直觉模糊数得分函数和精确函数值大小的比较,对区间直觉模糊数进行排序的方法。龚日朝和马霖源[13]基于得分函数和精确函数的本质内涵,运用概率论中全概率公式的思想构建了新的得分函数和精确函数,进一步完善了区间直觉模糊集理论以及多属性模糊综合评价与决策方法体系,使其应用于实际决策的能力得到进一步提升。
基于上述背景,本文根据旅游项目评估的特殊性,假设某一特定区域内存在多个旅游项目可供选择的情况下,首先构建特定区域内旅游开发项目选择的决策指标体系,运用序关系分析法(G1法)的思想提出了指标权重确定的群决策过程;其次,通过创新问卷调查民主测评方法,提出了运用区间直觉模糊数刻画指标民主测评统计结果的新方法,借助于区间直觉模糊集理论,构建了旅游开发项目选择的多指标属性模糊群决策模型。通过某区域旅游开发项目评估实例模拟计算,验证了新方法的可操作性和有效性。显然,这一研究对科学引导区域旅游产业可持续发展,顺利实现区域旅游整体规划,具有重大的理论和现实意义。
1 基本理论
在模糊决策理论中,基本概念有模糊集概念、直觉模糊集概念、区间直觉模糊集概念等。本文第二作者构建了新的得分函数和精确函数,进一步完善了区间直觉模糊集理论以及多属性模糊综合评价与决策方法。下面介绍基本概念。
定义1设X是一个非空论域,X上的区间直觉模糊集定义为:
A={〈x,uA(x),vA(x)〉|x∈X}
其中,uA(x)⊆ [0,1]和vA(x)⊆[0,1]分别表示X中元素x具有属性A的隶属度区间和非隶属度区间,且对任意x∈X,满足supuA(x)+supvA(x)≤1。隶属区间uA(x)和非隶属区间vA(x)所组成的有序区间对〈uA(x),vA(x)〉被称为区间直觉模糊数,并称区间
为犹豫区间。为简单起见,本文记uA(x) ≡[a,b],vA(x) ≡[c,d]。
该定义如果应用于指标属性特征的评价,隶属度区间uA(x)≡[a,b]可理解为在评价集体中,认为指标具有某属性特征的评价者占总人数的比率区间,而非隶属度区间vA(x)≡[c,d]为指标不具有某属性特征的评价者占总人数的比率区间。特别地,如果b+d<1,则1-b-d表示还有1-b-d比率的评价者对指标的评价不确定,也就是具有犹豫心理。由此理解,该定义能很好地刻画决策群体的意向,可通过统计调查的方式获得以区间直觉模糊数刻画的定性指标的评价值,显然具有很好的应用价值。
定义2设αi=〈[ai,bi],[ci,di]〉,i=1,2,…,n是n个区间直觉模糊数,对应权重为ω1,ω2,…,ωn,满足ω1+ω2+…+ωn=1,ω1≥0,i=1,2,…,n,则区间直觉模糊数的加权算术平均算子IIFWA定义为:
(1)
该定义运用在决策过程中,可以对多个以区间直觉模糊数刻画的指标,计算出它们的加权算术平均数,获得综合评价的结果,其依然是一个区间直觉模糊数,呈现了集体评价的意志。
定义3设α=〈[a,b],[c,d]〉为区间直觉模糊数,得分函数S(α)和精确函数A(α)分别定义为:
其中规定0/0=1,但02/0=0。
该定义将区间直觉模糊数转化为数值,得分函数用数值刻画出了人们对客观事物进行模糊评价的结果,同时通过精确函数刻画了模糊评价的精确度,为利用下面的定义对区间直觉模糊数的排序奠定了基础。
定义4设α0=〈[a0,b0],[c0,d0]〉和α1=〈[a1,b1],[c1,d1]〉为任意两个区间直觉模糊数,则
(1)当S(α0)>S(α1)时,α0>α1;
(2)当S(α0) (3)当S(α0)=S(α1)时,有 ①如果A(α0)>A(α1),则α0>α1; ②如果A(α0) ③如果A(α0)=A(α1),则需要进一步判断。 一般认为,旅游项目开发取决于两个维度:一是开发条件,主要包括:旅游资源自身价值、市场与区位条件、设施与服务条件等三个方面;二是预期效益,主要包括:经济、社会及环境效益[14-18]。特别是在我国经济从高速发展阶段转向高质量发展阶段的新时代,强调项目开发的预期经济效益、社会效益、环境效益是我国经济发展的战略要求。因此,本文基于政府决策视角,构建如下旅游项目投资决策评价指标体系(见表1)。 数据来源:作者计算。 指标权重是决策者最为关注的问题之一。理论上,权重确定分两大类方法:一是建立在大量样本统计数据基础上的客观赋权法,如:最大熵技术法、主成分分析法、多目标规划法等。二是在数据缺失条件下主要依据专家所掌握的理论与经验的主观赋权法,如:德尔菲法、AHP、模糊分析法、二项系数法、环比评分法、最小平方法、G1法等[19-23]。其中G1法无须构造判断矩阵,原理清晰,计算量小,当指标个数发生改变时不会改变权重大小关系,可以将来自不同领域专家对指标内涵的认识及其重要性理解的差异性纳入集体决策之中,能很好地应用于民主决策,因此,本文选取G1法确定指标权重。 假设决策小组由政府主管部门领导、旅游行业专家(包括资深导游)、学术理论界专家(包括经济类、管理类、旅游规划等专家)、旅游爱好者以及民间旅游项目投资商代表等N个决策者组成,决策者i的权重为di,满足did1+d2+…+dN=1,指标权重群决策过程如下: 第一步:确定指标重要性顺序,标准化权重确定分析框架。为了简化决策过程,本文采取决策小组共同研讨的方式确定指标重要性排序,表1中各级指标排序结果如下: (1)一级指标排序为:A1>A2; (2)二级指标排序为:B1>B2>B3,B4>B5>B6; (3)三级指标排序为:Ci1>Ci2>Ci3,i=1,2,3,4,5,6。 下面以三级指标权重为例说明权重确定方法。 表2 相邻指标重要性程度赋值参考 数据来源:作者整理。 (2)计算每个决策者i关于指标Cm,n,n=1,2,3的权重,公式如下①: (4) (3)对每个决策者所给出的权重进行加权平均,得到各三级指标的权重: (5) 根据表1指标体系,对于旅游项目这类决策问题,指标只能通过定性的方法刻画,具有不确定性和不精确性。对此,测度法一般分两类:一是定量测度法,即在规定的赋值范围内对每个指标人为地赋予一个确定性数值;二是定性等级测度法,即在规定的等级范围内对每个指标赋予某个等级。显然,前者取值为精确数,但是个体的主观性太强,容易造成极端评价事件,如:有的决策者可能赋值0,而有的决策者可能赋值100。因此,人们往往采取后者,如用A、B、C、D等等级评价,用以规避极端评价事件,体现模糊指标的模糊特性。当然这里也存在极端事件,有的赋值A,有的赋值D,但是,对于多个决策者给出的不同等级评价,这种等级赋值的离散程度显然要小很多。如果我们能采取科学的方法对统计数据归一处理,科学运用而不丢失统计数据所包含的信息,则后者必定优于前者。为此,本文基于区间直觉模糊数的内涵及其生成机理,提出一个新的指标测度方法。 该方法的做法是对每一个三级指标构建一个问卷调查表(或专家评价表),表中对每一指标设计两个选项,如“旅游资源自身价值”指标设置“高”与“低”两个等级,但同时对每一个等级均设置一个确认性提问,如果专家认为“旅游资源自身价值”肯定高,则在表中选择“肯定高”;如果认为比较高,则选择“比较高”。同样,如果专家认为“旅游资源自身价值”肯定低,则在表中选择“肯定低”;如果认为比较低,则选择“比较低”。特别地,如果认为不低也不高,或者对其不了解,则可以选择“弃权”选项。于是,根据每个专家的问卷调查表统计数据,即可获得指标评价的原始数据。如:假设有10位专家分别对某个旅游候选项目的“旅游资源自身价值”进行了评价,统计结果见表3。 表3 旅游资源自身价值问卷调查统计结果 数据来源:作者统计。 根据表3统计数据,我们可用区间直觉模糊数α=〈[0.4,0.6],[0.1,0.3]〉刻画统计结果。对此,可做如下解释: (1)区间[0.4,0.6]为隶属度区间,其下限0.4表示至少有40%的专家认为旅游资源自身价值高;区间的长度为0.2,表示有20%的专家认为“比较高”。换言之,区间[0.4,0.6]表示旅游资源自身价值高的调查结果在0.4到0.6之间。 (2)区间[0.1,0.3]为非隶属度,其下限0.1表示至少有10%的专家认为旅游资源自身价值肯定低;区间长度为0.2,表示有20%的专家认为比较低。换言之,区间[0.1,0.3]表示旅游资源自身价值低的调查结果在0.1到0.3之间。 (3)隶属度区间和非隶属度区间的上界之和为0.9,说明还有10%的专家给出了弃权评价。 从该方法的过程可以看出,一般地,表1中每个三级指标Cm,n都可获得一个区间直觉模糊数形式的评价结果,即: αmn=〈[amn,bmn],[cmn,dmn]〉 显然,运用该方法获得的指标评价数据,不仅可将评价者认知的模糊性纳入评价体系,呈现了决策群体的集体意志,而且可以克服传统等级评价方法存在的弊端。在实际工作中,可以通过提问的方式提醒评价者尽可能地减少其随意性,并降低评价者的工作难度和减少问卷调查数据统计的工作量,统计结果可以用区间直觉模糊数有效刻画。因此,本文称之为“区间直觉模糊评价法”。 根据三级指标的区间直觉模糊数统计数据,利用定义2区间直觉模糊数加权算术平均算子,首先计算得到各二级指标{Bik,i=1,2;k=1,2,3}的评价值,计算公式为: (6) 于是,根据定义3,可计算得分函数S(H)和精确函数A(H)。假设有n个待开发旅游项目Xi,i=1,2,…,n,则运用定义4,即可对项目的优劣进行排序,选择最优项目。 本文选取湖南省“十三五”旅游规划中拟开发的3个旅游项目:甲市明清古城三国水城项目、乙市文化旅游产业园项目、丙市旅游度假区项目,记为{甲、乙、丙}。采取群决策的方法从三个项目中确定最优开发项目。 关于专家权重的确定,本文假设每个专家的权重相同。从理论上来看,不同类别的专家,他们所拥有的专业知识和经验判断能力是不同的,尤其是在政府决策视角下,政府部门在决策中起着决定作用。因此,理论上专家权重设置应该差异化。但在现实集体会议决策过程中如果体现出这种差异化,从心理上必将影响低权重专家的情绪,从而影响集体民主决策。为此,本文采取通过设置不同类别专家的人数来解决这个问题,政府主管领导以及核心类专家的人数相对较多,确保决策核心群体拥有较大的权重,这样既解决了理论上的需求,又解决了现实工作的困境。于是,项目决策专家组由相关主管部门领导(3人)、旅游业规划专家(4人)、经济类专家(4人)、管理类专家(4人)、环境类专家(2人)、旅游项目民间投资商代表(1人)、资深旅行家(1人)、资深导游(1人)等20人组成。 根据表1的决策指标体系,运用2.2节中指标权重的决策专家小组群决策方法,通过20位专家的民主测评,我们得到了各级指标权重,见表1。同时,决策小组对甲、乙、丙三个项目按照指标体系,分别对每个三级指标独立评价,得到如下专家评价的统计结果,见表4。 表4 旅游项目三级指标的20位专家评价统计结果 数据来源:作者统计。 根据表4专家评价统计数据,我们可以获得以区间直觉模糊数表现的各三级指标统计结果,见表5。 根据表1三级指标权重和表5评价数据,运用公式(6)计算得到二级指标的评价值,见表6。 根据表1中二级指标权重值和表6二级指标评价数据,运用公式(7)和(8)计算得到一级指标的评价结果,见表7。 表5 旅游项目三级指标的专家评价结果 数据来源:作者计算。 表6 旅游项目二级指标评价计算结果 数据来源:作者计算。 表7 旅游项目一级指标评价计算结果 数据来源:作者计算。 最后,运用公式(9),计算得到三个项目的综合评价结果,见表8。 表8 旅游项目综合评价结果 数据来源:作者计算。 于是,根据定义4,按照得分值大小,我们可以得出结论:3个项目的排序为甲>乙>丙,项目甲是最优开发项目。经过20位专家的评价,支持项目甲开发的隶属度区间为[0.492 5,0.744 7],不支持其开发的非隶属度区间为[0.074 8,0.258 6]。根据其得分函数值,说明有75.79%的专家支持优先开发该项目。而对于项目乙和丙,支持开发的专家比例只有75.26%和74.87%,低于项目甲的支持率。 旅游项目决策是指在项目启动开发前,通过构建数学模型和管理方法,按照统一的指标体系和评价标准,在对项目作出客观、公正与准确评价基础上的一种经济活动。对于旅游项目开发决策问题,既要考虑项目开发的可行性,又要考虑其开发后的经济、社会、环境效益。尤其对于特定区域内旅游项目开发孰先孰后的问题,由于牵涉到特定区域政府管理部门、旅游项目多个利益相关者,可能无法由某一个利益主体来确定优先开发哪个项目,必须采取专家评审小组群决策的方式,才能确保旅游项目开发决策的公开、公平、公正。因此,采取专家评审小组群决策并创新决策模型,是解决现实和理论问题的必然选择。 本文首先提出了基于G1法的指标权重群决策方法,并基于问卷调查表设计的创新,开创性地构建了“运用区间直觉模糊数,刻画每个指标的民主评议统计结果”的新方法,然后借助区间直觉模糊集理论和方法,构建了旅游项目选择的多指标属性的模糊群决策模型。通过特定区域内多个旅游项目决策的实例计算,验证了本文提出的新方法的可操作性和有效性。 注释 ①公式的推导可参见,郭亚军著:《综合评价理论与方法》,科学出版社2002年版。2 旅游项目群决策过程与方法
2.1 构建评价指标体系
2.2 确定评价指标权重
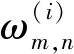
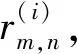


2.3 选择指标测度

2.4 构建多属性综合评价测度模型
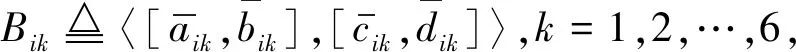
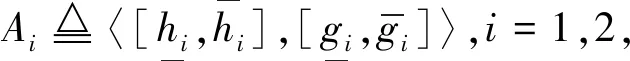
3 决策实例
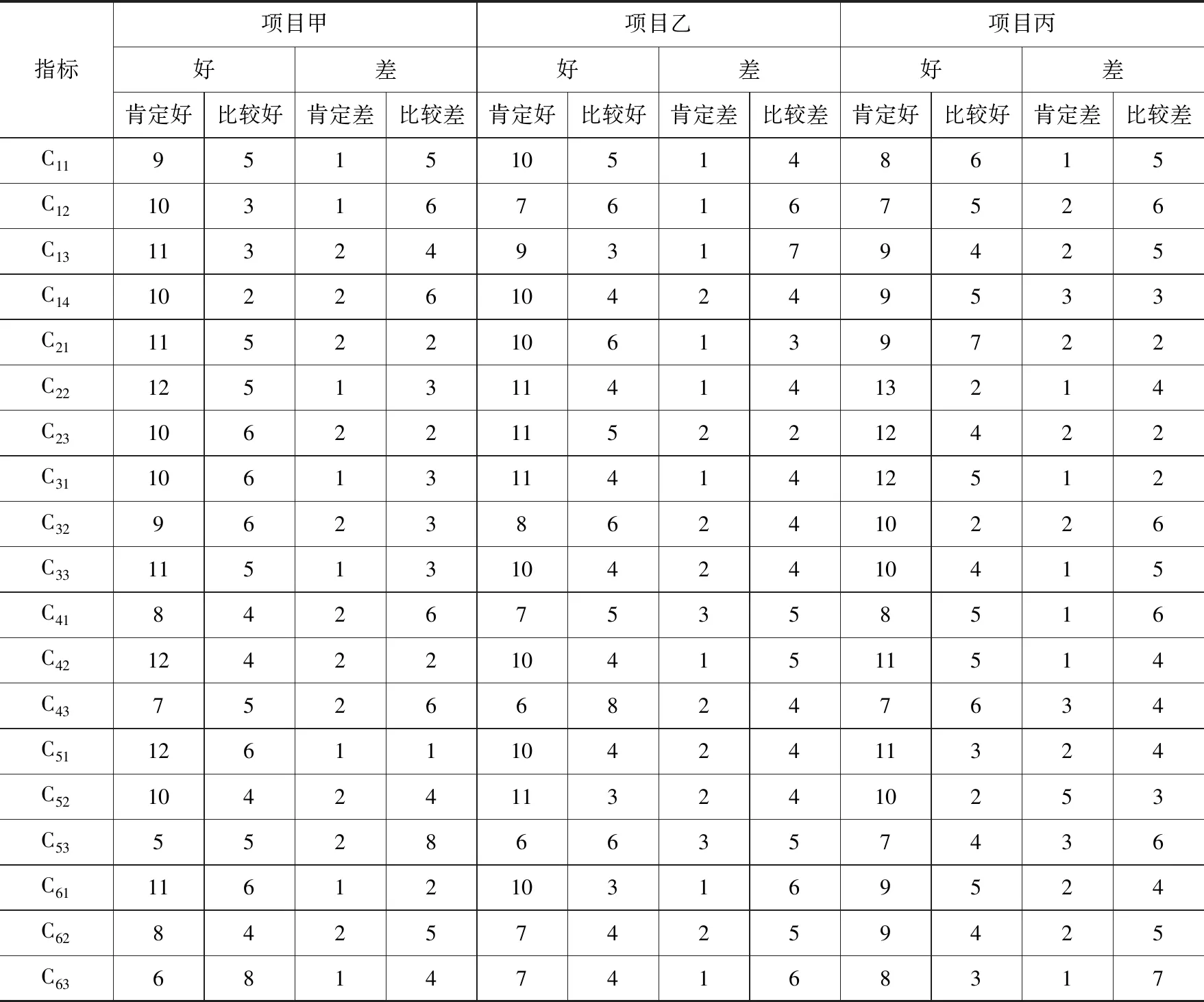
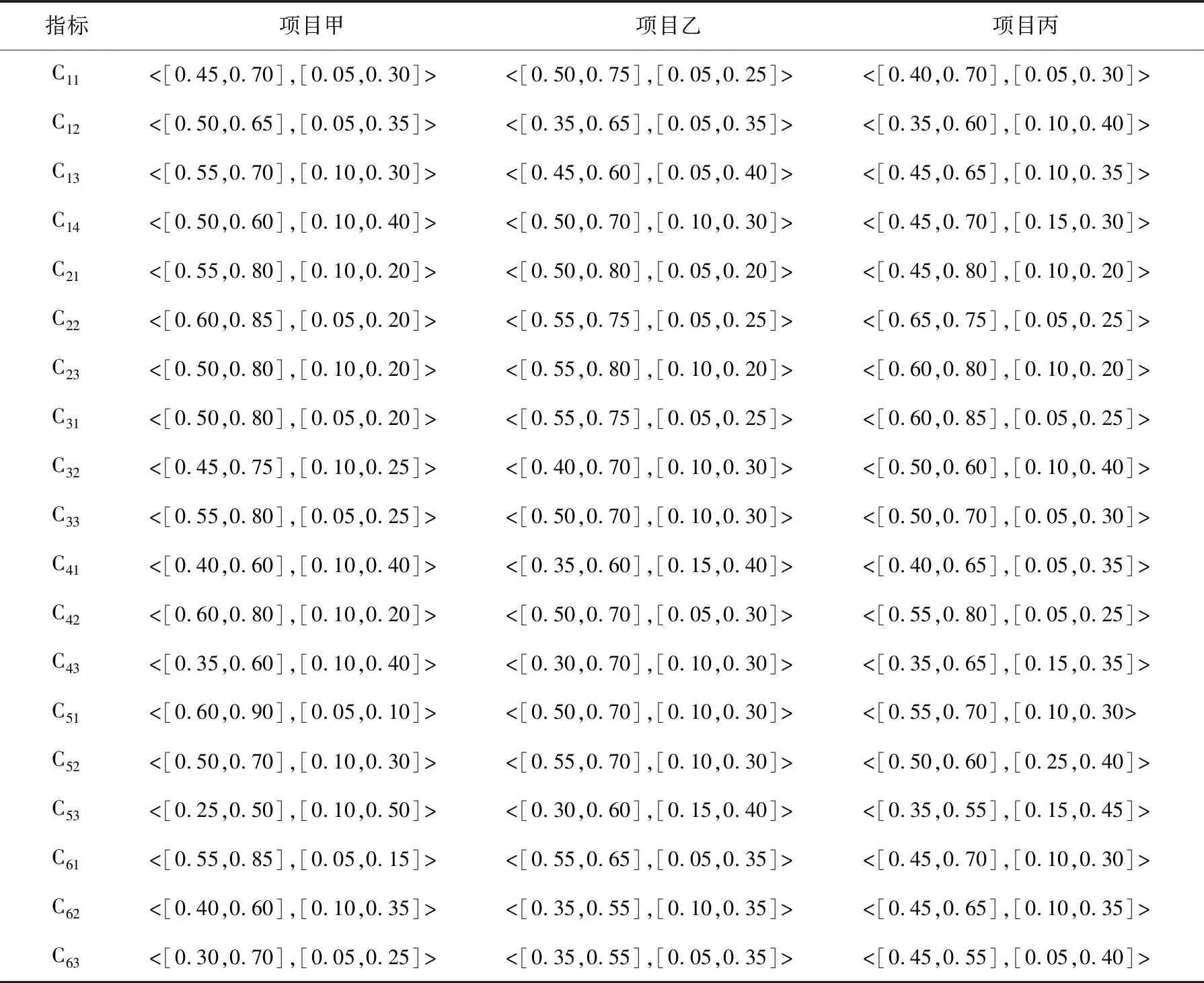
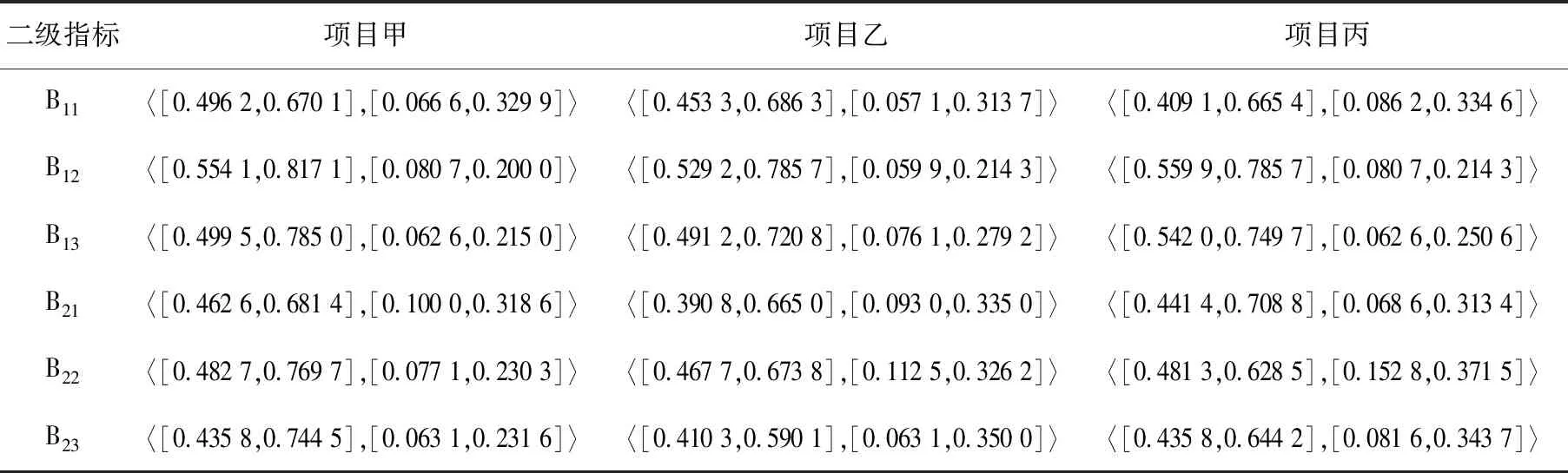


4 结论

