一种改进的非负矩阵最大特征值的C-W算法

商钰莹，张美黎，吕洪斌，王信存

(1.北华大学数学与统计学院，吉林吉林 132013;2.辽东学院师范学院，辽宁丹东 118003)

1 引 言

非负矩阵是一个重要的矩阵类，它在数值分析、概率统计、组合分析、动态规划、运筹学、数理经济和人口统计学等方面都具有重要应用［1-2］，而对非负矩阵最大特征值的估计与计算又是非负矩阵理论中的经典内容，在数值代数中具有重要意义.

设 A=(aij) ∈ 瓘n×n，记 N={1，2，…，n}，ri(A)=i∈ N，I是单位矩阵，σ(A)={λ1(A)，λ2(A)，…，λn(A)}表示矩阵A的谱集，ρ(A)=表示矩阵A的谱半径.若A=(aij)∈Rn×n，且 aij≥0，i，j∈N，则称A为非负矩阵，记为A∈Nn.由Perron-Frobenius定理［1-2］知ρ(A) ∈σ(A)，称为非负矩阵A的最大特征值，也称ρ(A)为非负矩阵A的Perron根，其对应的特征向量可取为非负的，也称为非负矩阵A的最大特征向量.

定义1［3］设A，如果存在置换矩阵P，使得，其中B为A的r×r阶主子矩阵，D为A的(n－r)×(n－r)阶主子矩阵(其中1≤r＜n)，则称矩阵A是可约的，否则称矩阵A是不可约的.

关于非负矩阵谱半径(最大特征值)的界，有著名的Perron-Frobenius定理:

定理1［1-2］设A=(aij)∈Nn，ρ(A)是A的谱半径，则

幂法是求矩阵最大特征值与最大特征向量的经典数值方法［4］，但是幂法的最大缺点［4］就是收敛速度比较慢，当然也有条件限制.关于不可约非负矩阵最大特征值的算法，文献［5-7］给出了不同的迭代方法.本文利用不可约非负矩阵及C-W函数的性质，给出了一种改进的计算不可约非负矩阵最大特征值的C-W算法.

2 C-W函数

令 R+为全体非负实数集合，记={x=(x1，x2，…，xn)T∈ Rn:xi≥ 0，i=1，2，…，n}，Hn={0}.

定义2［2］设A∈Nn不可约，下列两个从Hn到R+的函数

若存在某个i，使得xi=0且(Ax)i≠0，则定义GA(x)=+!，称为伴随于矩阵A的Collatz-Wielandt函数，简称为矩阵A的C-W函数.

关于C-W函数有如下性质:

定理2(C-W定理)［2］设FA(x)，GA(x)是n阶不可约非负矩阵A的C-W函数，则

(ⅰ)FA(x)及GA(x)都是零次齐次式.

(ⅱ)如果d是满足Ax－dx≥0，x∈Hn的最大实数，那么d=FA(x);如果e是满足Ax－ex≤0，x∈Hn的最小实数，那么e=GA(x).

(ⅲ) 如果 x ∈ Hn，且 y=(I+A)n－1x，那么 FA(y) ≥ FA(x)，GA(y) ≤ GA(x).

(ⅳ)FA(x)≤s，GA(x)≥t，其中s、t分别为A的最大、最小列和.

3 迭代格式与收敛定理

设 A ∈ Nn不可约，令 B=(A+ αI)n－1，α ＞ 0，则由非负矩阵的经典理论知 B 为正矩阵［1，2］.对任取的初始向量x(0)∈Hn，定义如下迭代格式

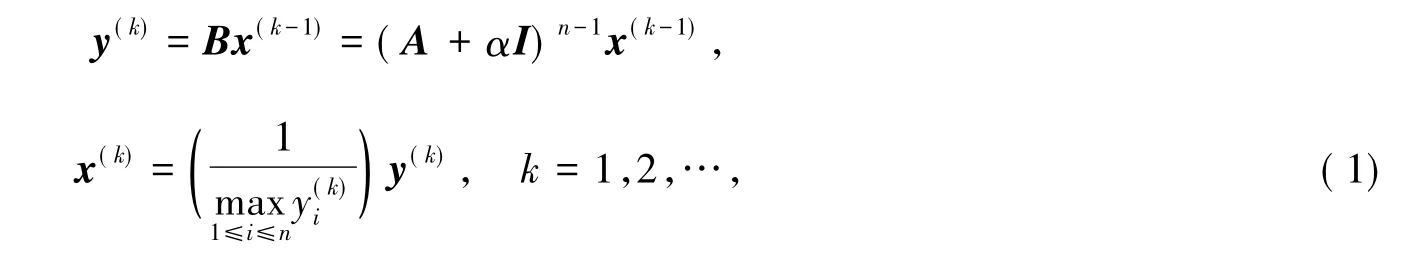
式中:x(k)是把y(k)标准化所得的向量，即 x(k)!=1.下面将证明由此产生的向量序列{x(k):k=1，2，…}收敛于A的一个最大特征向量，正数列{FA(x(k)):k=1，2，…}及{GA(x(k)):k=1，2，…}都收敛于A的最大特征值ρ(A).

定理3设A∈Nn不可约，B=(A+αI)n－1，α ＞ 0，{x(k):k=1，2，…}为由迭代格式(1)所得的向量序列，则

证明:按C-W函数的定义，对任意正整数k有

再由C-W定理(ⅳ)知{FA(x(k)):k=1，2，…}是有上界的单调不减实数列，从而存在极限，令

由于x(k)∈Hn且B=(A+ αI)n－1，α ＞ 0为正矩阵，故Bx(k)为正向量，从而x(k+1)为正向量，k=1，2，….又因 x(k+1)=1，故{x(k):k=1，2，…}是有界实向量序列，从而存在它的一个收敛子序列{u(k):k=1，2，…}.记=z，则z是正的标准向量，且满足Az－lz≥0.

假设 Az － lz≠ 0，由 Bz=(ρ(A)+ α)n－1z，α ＞ 0，有

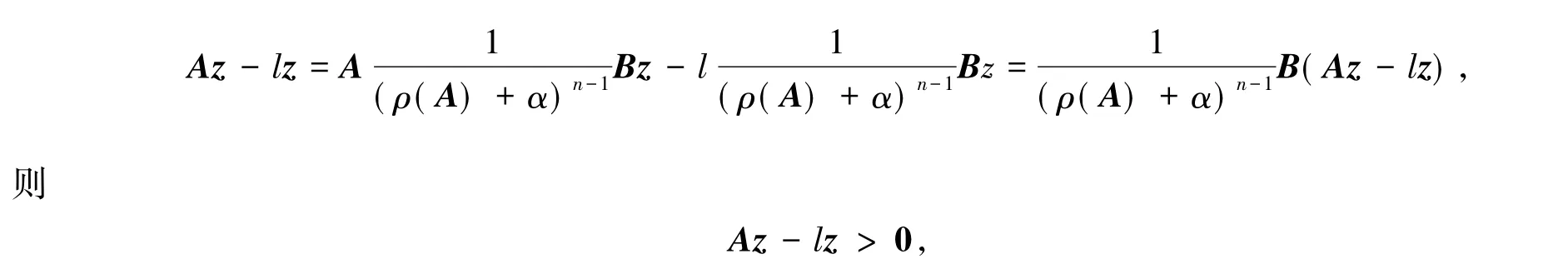
从而由C-W函数的性质有l＜FA(z)=FA()=(u(k))=l的矛盾.所以Az－ lz=0，也就是Az=lz，即正向量z为不可约非负矩阵A的一个正特征向量.由非负矩阵的经典理论［1-2］可知，任何不可约非负方阵A的任何正特征向量都对应于A的最大特征值，并且不计数量倍数的差别是唯一的.据此得z=是矩阵A的唯一的标准最大特征向量，(x(k))=ρ(A)是矩阵A的最大特征值.

再由C-W迭代格式(1)的定义可知x(k+1)连续依赖于x(k)，从而由=z得到l=z.k

同理可证，{GA(x(k)):k=1，2，…}是有下界的单调不增实数列，从而存在极限(x(k))=h，满足Az－hz≤0，其中z=为正向量.再利用与上面类似的推理又得Az=hz及h=ρ(A)，即(x(k)) 为矩阵A的最大特征值.证毕.

推论1设A∈Nn不可约，{x(k):k=0，1，2，…}是由迭代格式(1)所得到的向量序列，则0＜FA(x(0))≤…≤FA(x(k))≤FA(x(k+1))≤…≤ρ(A)≤…≤GA(x(k+1))≤GA(x(k))≤…≤GA(x(0)).

4 算法及分析

步0 给出不可约非负矩阵A=(aij)n×n，ε ＞ 0，x(0)=(1，1，…，1)T∈Rn(或Hn中任何向量);

步1 计算 B=(A+ αI)n－1，α ＞ 0;

步4 如果GA(x(k))－FA(x(k))＜ε，停止迭代，输出ρ(A)= (GA(x(k))+FA(x(k)))/2，否则转至步2.下面应用MATLAB通过具体例子分析上述算法.

例1设

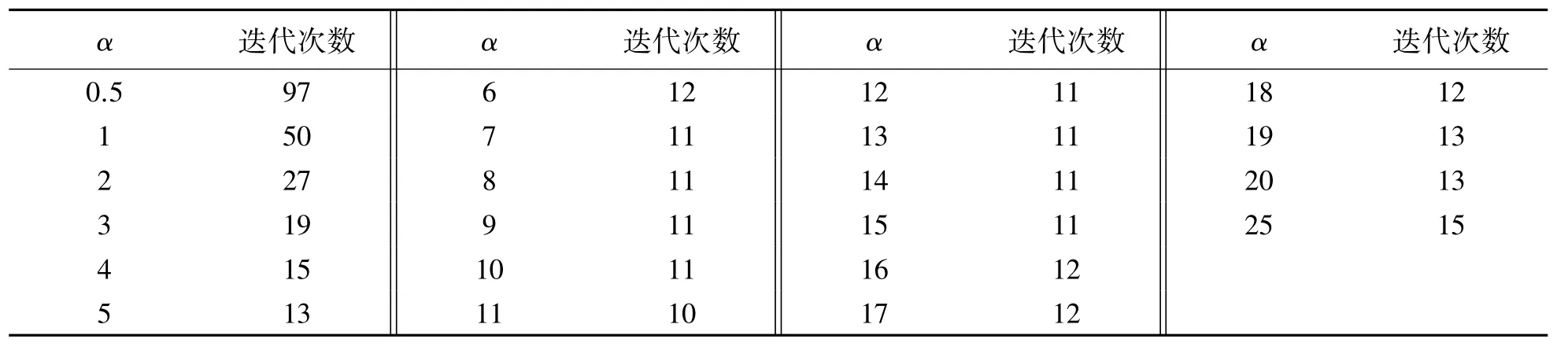
表1 不同的α＞0计算ρ(A)的迭代次数Tab.1 Calculate the number of iterations of ρ(A)with different α ＞ 0(ε =10－5)

由表1知，当α=11，ε=10－5时，本文算法的收敛速度是文献［6-7］算法的5倍.

对于一般的可约非负矩阵A∈Nn，可以将其化为可约标准形，再对对角块矩阵应用本文算法，求得其最大特征值ρ(A).