一类四阶微分方程的非线性混合边界条件的奇摄动问题

刘 燕

(安徽师范大学皖江学院，安徽芜湖 241000)

1 引 言

非线性奇摄动问题的研究受到国内外学者的密切关注，多种近似方法不断地得到优化，包括合成展开法、边界层函数法、伸展变量法等，使得非线性奇摄动在天体力学、弹体力学、生物学、声学等领域有了广泛应用［1-4］.近年来，许多学者在非线性奇摄动相关领域做了大量工作，其中文献［5-9］研究了分离型边界条件的非线性微分方程的奇摄动问题，此时奇摄动问题的定解条件只限于分离型的边界条件，还未涉及混合型的边界条件;2014年，文献［10］研究了一个四阶微分方程的非线性混合边界条件的奇摄动问题

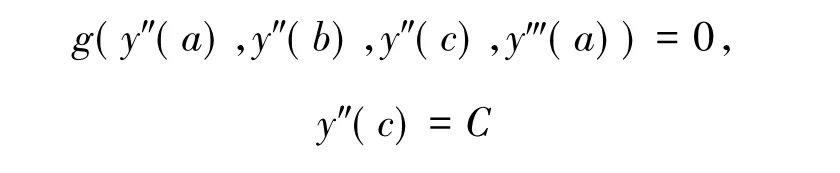
解的存在性和渐近估计;2015年，文献［11］又研究了一个三阶微分方程的非线性混合边界条件的奇摄动问题

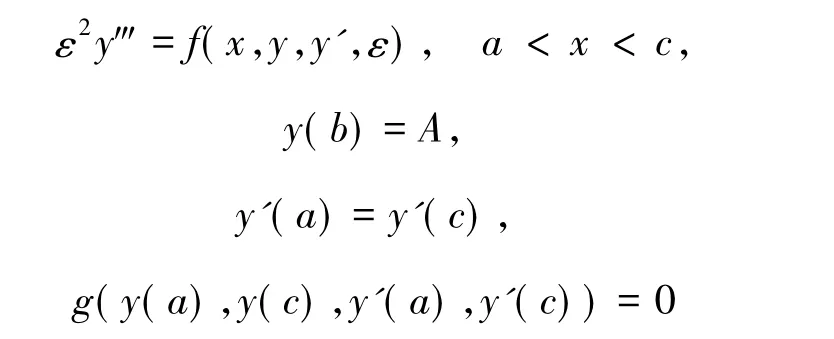
解的存在性和渐近估计.非线性混合型边界条件奇摄动问题比非线性分离型边界条件奇摄动问题要复杂，因此，对于非线性混合边界条件的奇摄动问题的研究相对较少.受以上文献的启发，本文运用合成展开法和微分不等式理论考虑如下一类非线性混合边界条件的奇摄动问题

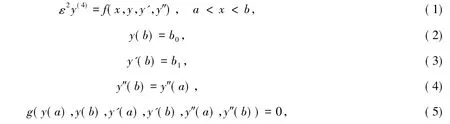
其中:a，b，b0，b1均为常数，0 ≤ a ＜ b，ε 是正的小参数.

现作如下假设

H1)问题(1)～(5)的退化问题

在［a，b］上存在充分光滑的解Y0=Y0(x)，且函数方程

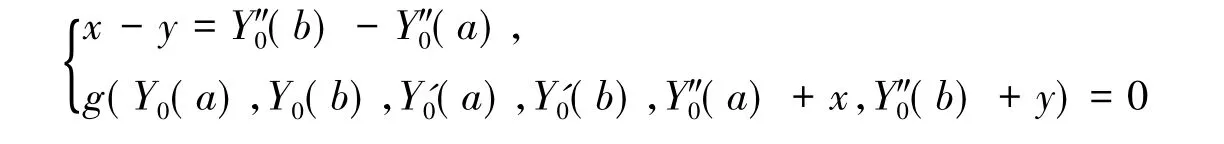
有唯一的一对正解x=V0，y=W0;

H2) 函数f(x，y，y'，y″) 关于其变元在相应的区域内充分光滑，且存在正常数 l0，l1，l2，使得 － l2≤fy≤

H3)g(x，y，z，p，q，r) 关于其变元在相应的区域内充分光滑，gx≤0，gy≤0，gz≥0，gp≥0，且存在正常数 δ0使得

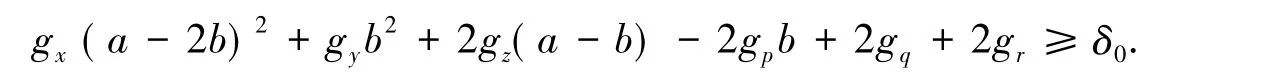
2 形式渐近解的构造

设问题(1)～(5)的外部解的形式渐近式为

将式(9)代入式(1)，按ε的幂展开f，可得到

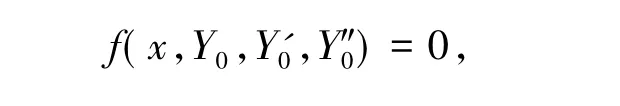
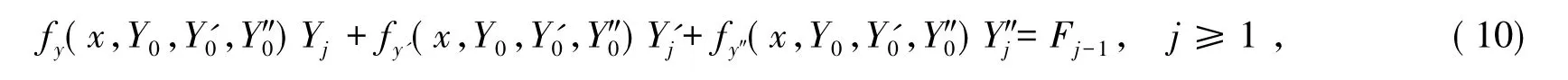
其中Fj－1(j≥1)是由Y0，Y1，…，Yj－1依次确定的函数.这样就得到外部解的递推方程.由于外部解的递推方程是一个二阶方程，一般不满足式(4)和(5)，所以需要在x=a处和x=b处构造边界层校正项.

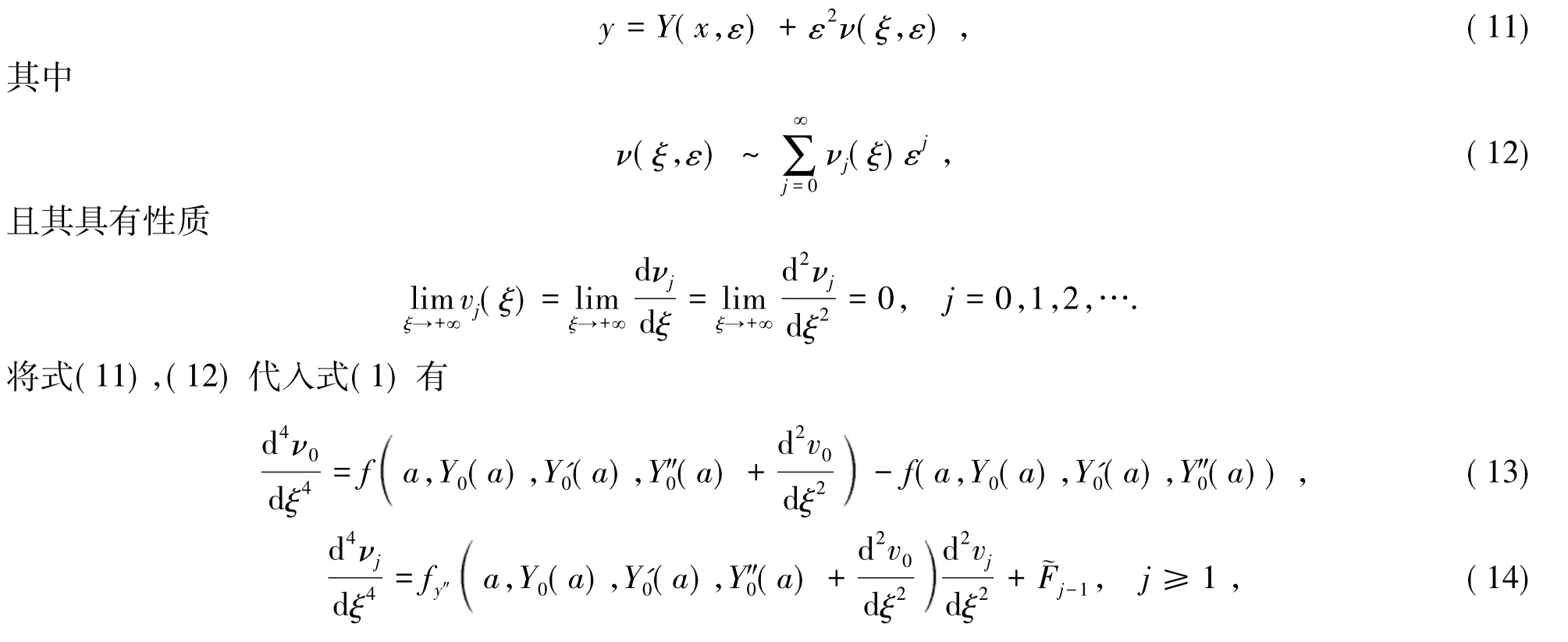
其中珘Fj－1(j≥1)是ξ的某个多项式与若干个νk(k≤j－1)及其各阶导数的乘积之和.

为了确定关于Yj(x)，vj(ξ)，ωj(η)的定解条件，首先将式(15)代入式(2)和(3)得

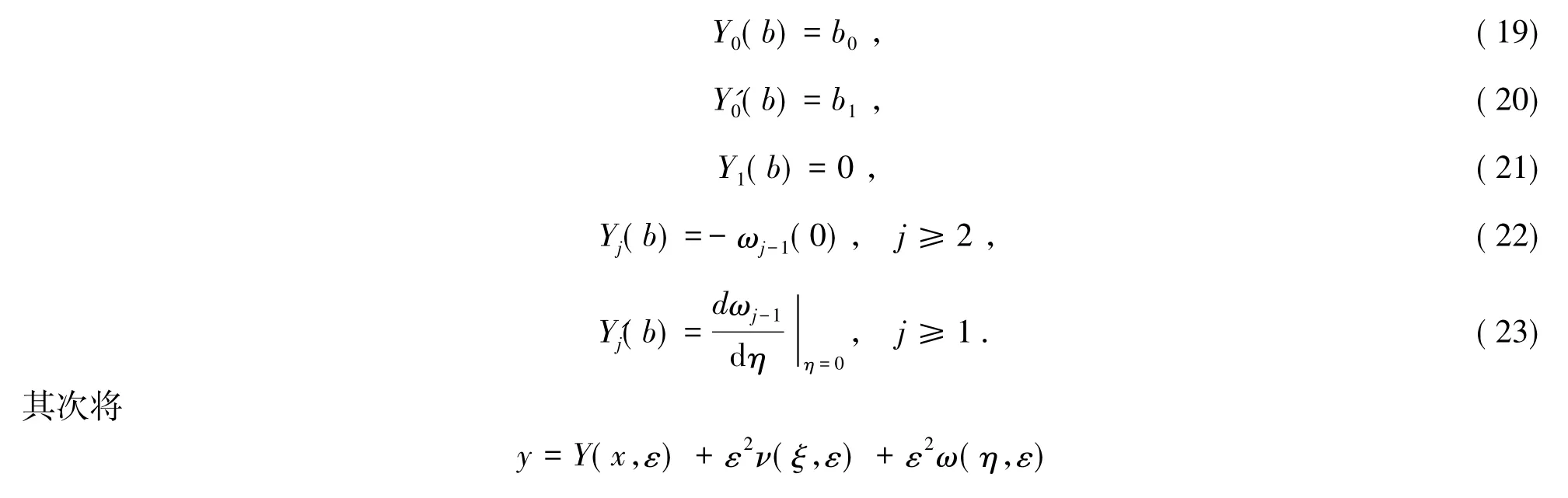
代入式(4)和(5)得

其中Gj－1(j≥1)是确定的数值.由假设H1)，H2)及式(24) ～(25)可求出

其为问题(1)～(5)的退化问题(6)～(8)，由假设H1)可知其解存在为Y0=Y0(x).

根据上面求得的递推方程(10)，(13)～(14)，(17)～(18)和定解条件式(19)～(27)以及

运用交替迭代的方法可依次求出 Yj(x)，νj(ξ)，ωj(η).由式(13)，(17)和假设 H2)知

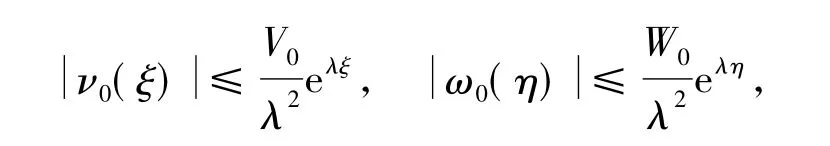
引进光滑函数ψ(x)∈C!，使得

这样就得到问题(1)～(5)的m阶形式渐近解.

3 引理和主要结果

定义 1［12］若函数 α(x)，β(x) ∈ C4［a，b］满足

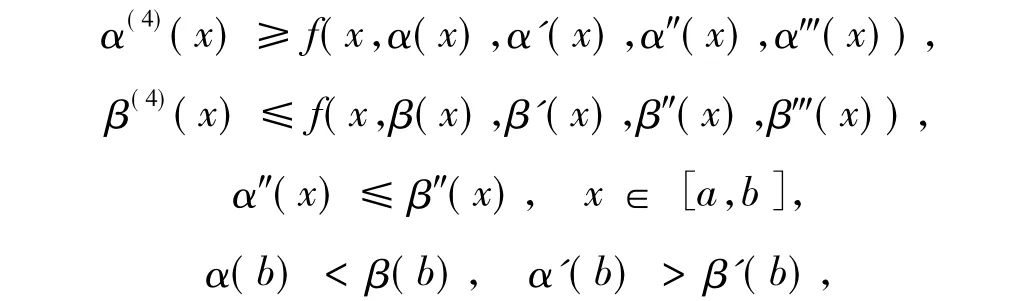
则称α(x)，β(x)分别为边值问题

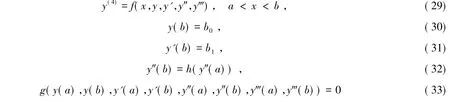
的上下解.

在上述定义下有

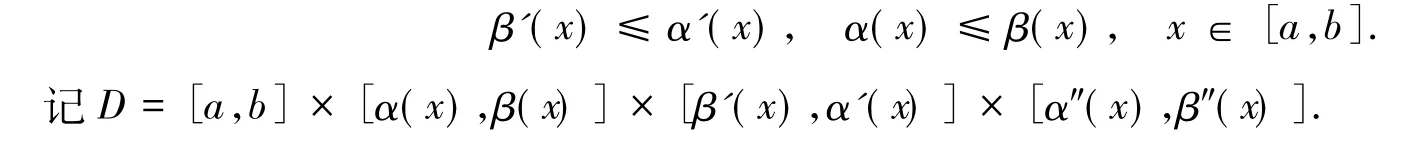
定义 2［12］若 f(x，y，y'，y″，y) ∈ C［D × R，R］满足

引理1［12］若边值问题(29)～(33)满足如下条件:

(ⅰ)存在如定义1所述的上下解α(x)，β(x);

(ⅱ) 函数 f(x，y，y'，y″，y) 在 D 上关于 α(x) 和 β(x) 满足 Nagumo条件;

(ⅲ) 函数 f(x，y，y'，y″，y) ∈ C［［a，b］× R4，R］关于 y'单调不减，关于 y 单调不增;

(ⅳ)h 为［α″(a)，β″(a)］→［α″(b)，β″(b)］的同态映射，且满足

(ⅵ) 函数 g(x，y，z，p，q，r，s，t) 在R8上连续，且关于变量z，p，t单调不减，关于变量x，y，s单调不增，同时满足

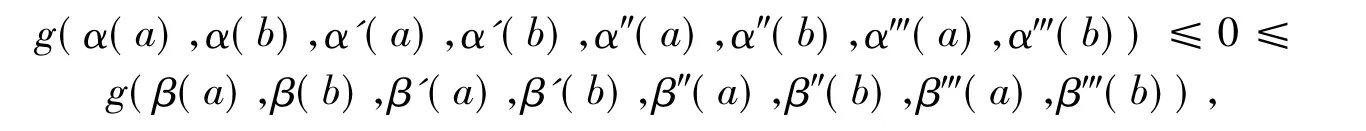
则边值问题(29) ～(33)存在解y(x)∈C4［a，b］满足

定理1在假设H1)～H3)成立下，则存在ε0＞0使得对任意的0＜ε＜ε0，边值问题(1)～(5)有解 y=y(x，ε) ∈ C4［a，b］满足

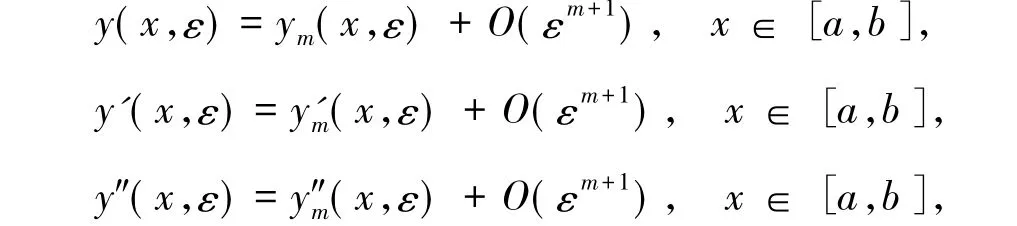
其中ym(x，ε)由式(28)给出.

证明:构造界定函数

其中r为待定的充分大的正常数.显然有

另外，由微分中值定理，存在正常数M1，使得

其中θi(i=0，1，2)介于与β(i)之间.

当x∈［a，a+σ］时，由外部解和左边界层的构造知，存在正常数M2，M3使得

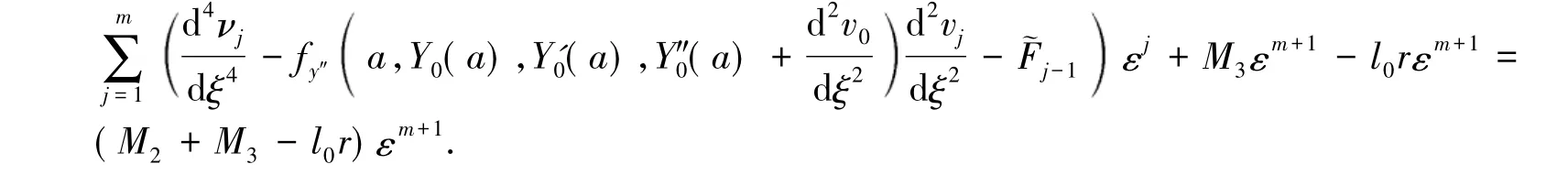
当x∈［b－σ，b］时，由外部解和右边界层的构造知，存在正常数M4，使得

当 x∈［a+σ，b－σ］时，由vj(ξ)，ωj(η)的边界层性态知，存在正常数M5和ε0，对任意的0 ＜ ε≤ε0有

则有 ε2β(4)－ f(x，β，β'，β″) ≤ 0，x ∈［a，b］.

类似地，对式(34) 给定的r有ε2α(4)－ f(x，α，α'，α″) ≥0，x∈［a，b］.由引理1可知，对式(34) 取定的r，当 0 ＜ ε ≤ ε0时，边值问题(1) ～ (5) 存在解 y(x，ε) ∈ C4［a，b］，满足.

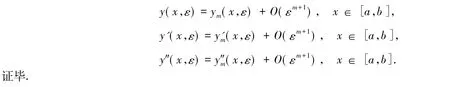
4 例 子

考虑如下混合边值条件的四阶微分方程的奇摄动问题

满足假设条件H1) ～H3)，事实上，l0=4，l1=l2=1.

问题(35)～(39)的退化问题为