基于MCKD与CEEMDAN的声信号故障特征提取方法

申博文，王华庆，唐 刚，宋浏阳

(北京化工大学 机电工程学院，北京 100029)

传统滚动轴承故障诊断基于振动信号实现，但对于双转子轴承等特殊部件，因信号传递路径复杂，直接通过加速度传感器获取故障信号具有一定难度.在机械设备工作过程中声音信号伴随着振动信号产生，声音信号中亦带有大量设备运行状态的信息,设备发生故障时声音信号频谱会有所变化.利用设备工作过程中产生的异常噪音信号检测设备的运行状态的方法，相比于其他方法具有不接触设备和操作简单等优点.

由于声音信号信噪比较低，故存在故障特征直接提取较困难等缺陷.针对声音信号信噪比较低这一问题涌现了多种降噪方法.Donoho等提出的小波阈值去噪算法[1]通过设置合适阈值区分信号和噪声，但是当原信号中某细节处的小波系数与噪声较多处的小波系数接近时，有用信号易被当成噪声滤掉；Huang等[2]提出的集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)算法通过加入高斯白噪声避免模态混叠，但是最终加入的噪声有可能无法完全消除；完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition, CEEMD)算法[3]通过加入正负成对的辅助白噪声来抵消只加入正态白噪声导致的问题，但是增加了算法复杂度且没有完全解决模态混叠问题；Torres等[4]提出的自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)算法可以利用自适应噪声有效减少计算成本并克服模态混叠问题.

多模态分解降噪方法在声音信号降噪方面较为有效，但当采用多模态分解降噪方法时，需要对多个模态分量逐个观察[5-6].Qian等[7]以峰值因子和裕度等多指标融合后的指标参数为诊断依据对飞机发电机进行故障诊断，取得了良好的诊断准确率；Qing等[8]利用经验模态分解(Empirical Mode Decomposition, EMD)滤波处理后的最大谱峭度分量构成的重构信号，结合匹配追踪算法提取出了故障冲击成分.峭度与其他时域参数相比，对冲击信号更为敏感，适用于轴承早期故障的诊断.轴承故障声音信号中存在的噪声具有复杂性和多样性，很大程度上增加了故障诊断的难度，最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution, MCKD)算法[9]作为一种性能良好的降噪方法已经引起了科研工作者的广泛关注.MCKD算法以相关峭度作为评价指标，可在一定程度上降低信号中的噪声成分，提升原始信号的峭度，从而充分突出轴承故障信号中被噪声淹没的周期冲击成分.基于此，本文综合运用CEEMDAN和MCKD两种方法分解声音信号，根据峭度值选取最优分量并求Hilbert包络谱，以准确提取故障特征频率，实现了基于声信号的自适应故障诊断，在一定程度上降低了故障诊断的复杂程度.

1 基本理论

1.1 改进算法流程

图1 故障诊断的流程图Fig.1 Flow chart of fault diagnosis

本文提出的改进算法的流程如图1所示.首先，使用MCKD算法寻找最优滤波器，增强故障声音信号中的周期冲击成分.降噪后信号经CEEMDAN算法分解得到若干模态分量，选取所有模态分量中的前8个模态分量进行峭度值计算，并求取峭度值最大模态分量的包络谱.在包络谱中提取故障特征频率，即可确定轴承故障类型.

算法中使用的峭度是一个无量纲参数，计算公式如下：

1.2 最大相关峭度解卷积

当轴承发生故障时，由于出现局部碰撞，会产生周期性冲击信号x，该冲击信号x传递到传感器上时，由于传输路径的影响会逐渐衰减，并且会掺杂大量的噪声成分e.假设路径传输衰减响应为h，则传感器拾取到的实测信号y可表示为

y=h·x+e，

(1)

而MCKD算法通过实测信号y恢复冲击信号x，从而达到抑制噪声和突出故障冲击成分的目的，即

(2)

MCKD算法以相关峭度作为评定恢复信号x性能的指标，当相关峭度达到最大时，获得MCKD算法的最终结果.对于任意信号yn，相关峭度定义为

(3)

其中：T为冲击信号的周期；M为位移数.

求解方程后得到的滤波器系数组合用矩阵形式表示如下：

(4)

式中：r=0，T，2T，…，mT，

将得到的滤波器系数组合f代入式(2)，即可得到周期性冲击信号x.

1.3 CEEMDAN算法

在CEEMDAN算法中，分解得到的模态分量用IMFk表示，IMF1与EEMD中IMF1的计算方法相同[10-11].定义操作符Ej(·)表示通过EMD计算获得的给定信号的第j个模态分量，ωi为满足N(0，1)的高斯白噪声，如果X[n]是待处理的信号，则CEEMDAN算法可描述如下：

(1) 利用EMD算法分解得到的第1个模态分量为

(5)

(2) 在第1阶段(k=1)计算第1个余量，得

R1[n]=X[n]-IMF1[n]；

(6)

(3) 对于k=1，2，…，K，计算第k个模态分量，得

(7)

(4) 对于k=2，3，…，K，计算第k个余量，得

Rk[n]=R(k-1)[n]-IMFk[n]；

(8)

(5)k=k+1，返回第(4)步，重复第(3)步和第(4)步，直到残差余量不适合被分解时，停止分解.最终的余量满足

(9)

2 仿真实验分析

机械结构发生故障时，故障信息既可以通过振动传递，也可以通过声音传递.机械设备运行中的声音信号是振动信号的延伸，当设备状态发生改变的时候，声音信号特性也随之改变.在轴承故障诊断中，Zhou等[12]提出的声信号故障诊断方法中采用故障特征频率作为诊断依据，此时的故障特征频率求解方法与振动信号故障特征频率求解方法一致，因此采用故障特征频率作为声信号故障类型诊断依据具有可行性.为验证提出方法的有效性，构建如下模型来模拟轴承故障时的声音信号：

(10)

表1 仿真信号经CEEMDAN及改进方法处理后各分量的相关峭度

式中：S(t)为周期性指数衰减冲击信号，频率为72Hz.选取信号长度为5000，在上述冲击信号中加入5dB高斯白噪声.仿真信号的时域波形和包络谱如图2(第388页)所示，A为幅值.

由结果可知直接通过包络解调方法很难提取出故障特征频率.仅使用CEEMDAN方法对信号进行处理，选取模态分量中的前8个分量进行峭度计算，所得的各分量峭度如表1所示.根据峭度最大原则，选择IMF8进行包络分析，分析结果如图3所示，此时峭度最大分量IMF8的包络谱中并不能有效地提取故障特征频率.

对同一仿真信号采用文中所提出的改进方法进行处理，各分量的相关峭度如表1所示.根据峭度值最大原则选取IMF1进行包络变换，IMF1时域波形及包络谱如图4所示.结果表明，与仅进行CEEMDAN处理相比，文中所提算法可以根据峭度值有效选择最优分量进行故障诊断.

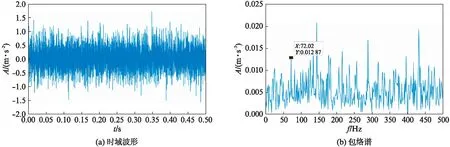
图2 仿真信号的时域波形和包络谱Fig.2 Time domain waveform and envelope spectrum of simulated signal

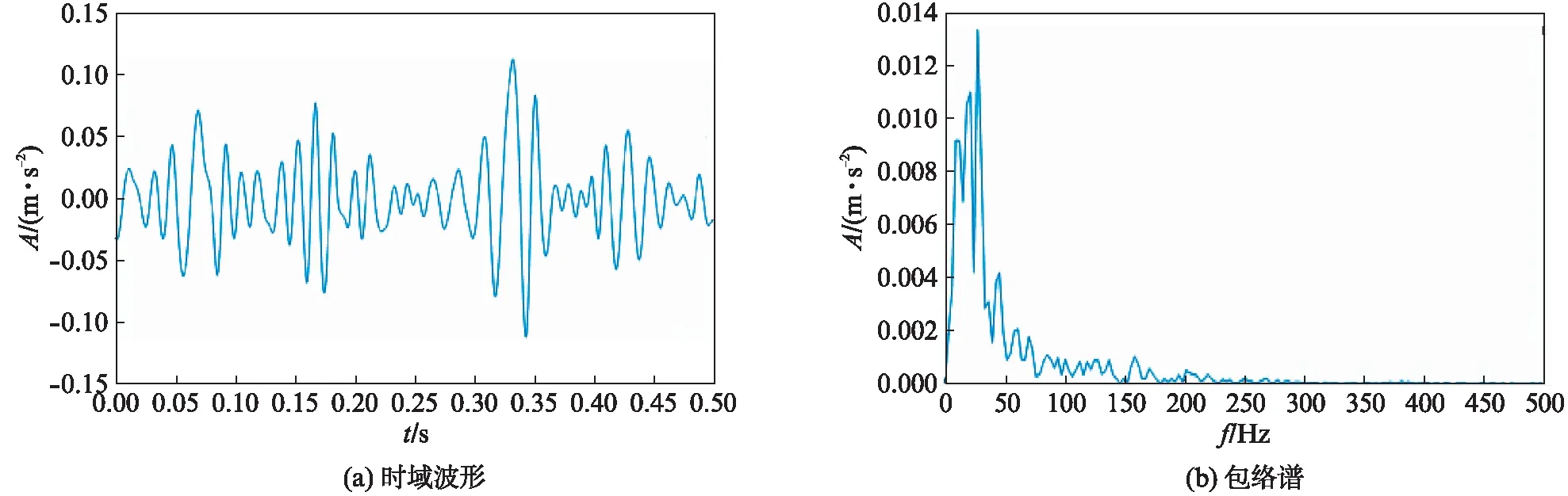
图3 仿真信号IMF8的时域波形和包络谱Fig.3 Time domain waveform and envelope spectrum of simulated signal IMF8

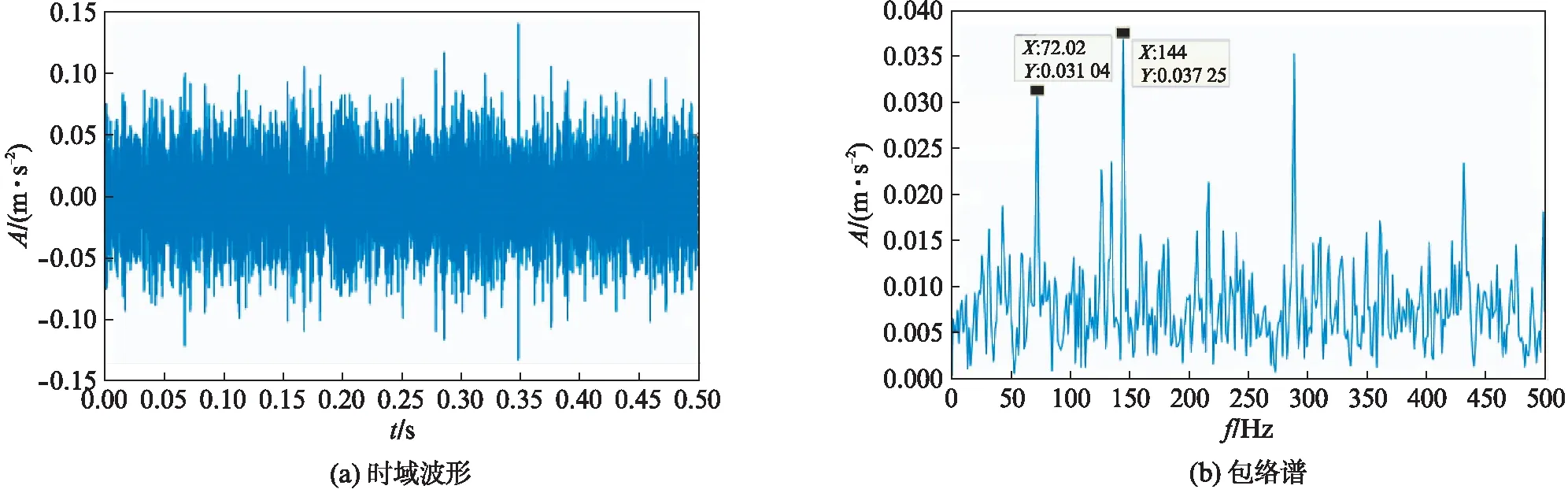
图4 仿真信号IMF1的时域波形和包络谱Fig.4 Time domain waveform and envelope spectrum of simulated signal IMF1

3 实验验证分析

我们还基于转子实验台进行了滚动轴承的故障诊断，来验证文中改进方法的有效性.实验装置结构如图5所示，声音信号传感器位置如图6所示.采集内圈故障轴承声音信号及外圈故障声音信号，实验中所用的内圈故障和外圈故障轴承如图7所示.设定实验台转速为400r/min，采样频率为96kHz.通过计算，

图5 实验装置平台Fig.5 Experimental device platform

图6 实验装置平台侧视图Fig.6 Side view of experimental device platform

图7 内、外圈故障轴承Fig.7 Fault bearing of inner and outer rings

在该转速下，轴承的转频fr为16.67Hz，内圈故障频率fi为44.75Hz，外圈故障频率fi为28.86Hz.特征故障频率的理论值通过相关公式[13]计算得到，同一故障类型的特征频率在转速恒定时保持不变，但实际值因实际工况影响会产生变动.当实际值在理论值附近时，可认为故障频率被有效提取.

3.1 轴承内圈故障

内圈故障声音信号时域波形及包络谱如图8所示.因噪声较大，周期性冲击被淹没，内圈故障特征频率无法从包络图中有效提取，影响故障类型的准确诊断.

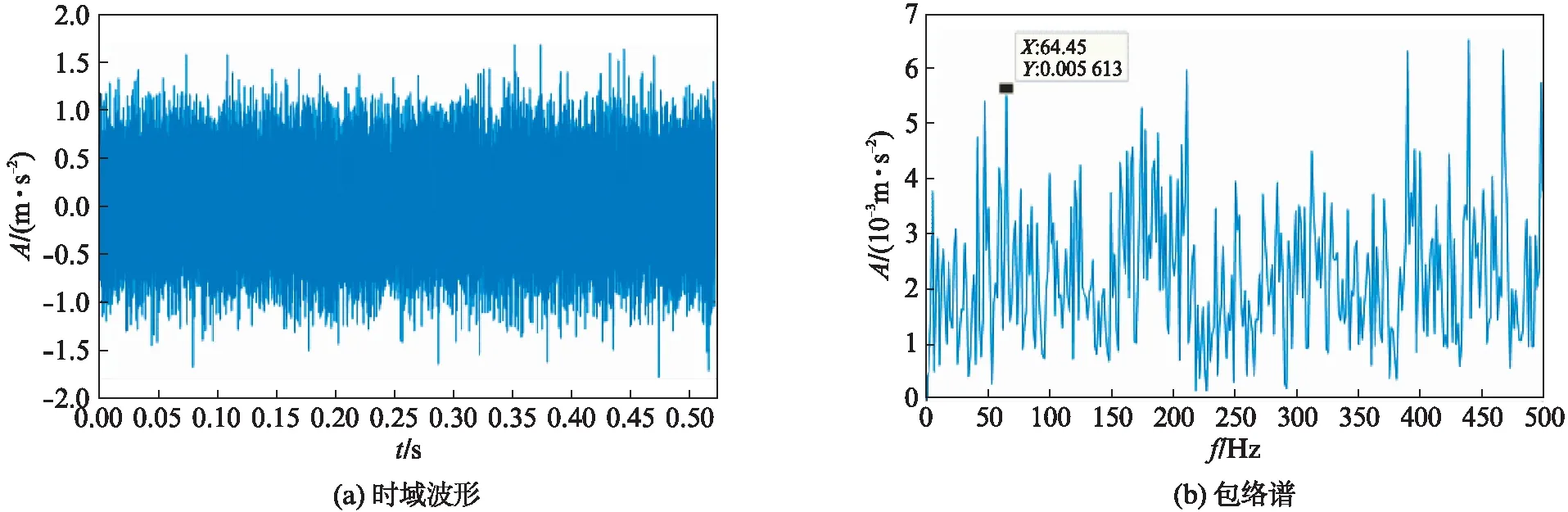
图8 内圈故障信号的时域波形和包络谱Fig.8 Time domain waveform and envelope spectrum of inner ring fault signal

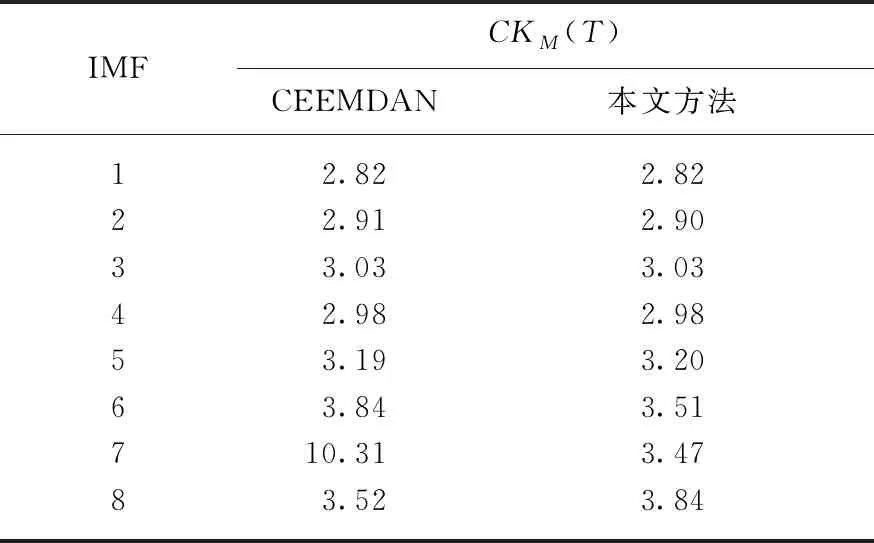
表2 内圈信号经CEEMDAN及改进方法处理后各分量的相关峭度

对内圈故障声音信号进行CEEMDAN分解，所得各分量峭度值如表2所示.分析峭度值最大的IMF7的时域波形和频谱图如图9(第390页)所示，频率36.62Hz处幅值明显，但是该频率并非故障特征频率，即故障特征频率不能被有效提取，无法通过原始方法进行故障类型诊断.图10(第390页)为通过文中改进方法处理后的有效模态分量的时域波形及频谱图，该模态分量选择依据见表2.对比图9与图10，时域波形中依旧存在较大噪声，周期性冲击不明显.但通过包络谱图可见，转频成分的干扰程度降低，故障频率45.41Hz得到了增强，且该频率为内圈故障特征频率，同时干扰频率成分减少，可以有效地进行故障诊断.因此，试验结果证明了文中所提改进方法的有效性.

图9 内圈信号经CEEMDAN处理后IMF7的时域波形和包络谱Fig.9 Time domain waveform and envelope spectrum of inner ring signal’s IMF7 processed by CEEMDAN

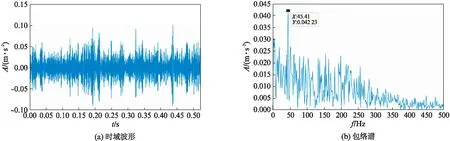
图10 内圈信号经改进方法处理后IMF8的时域波形和包络谱Fig.10 Time domain waveform and envelope spectrum of inner ring signal’s IMF8 processed by the improved method

3.2 轴承外圈故障

外圈故障信号的时域波形和包络谱如图11所示，从时域波形图中难以提取故障冲击成分.外圈故障声音信号频谱图中突出频率成分均不是故障特征频率，故无法准确提取故障特征频率.

图11 外圈故障信号的时域波形和包络谱Fig.11 Time domain waveform and envelope spectrum of outer ring fault signal

表3 外圈信号经CEEMDAN及改进方法处理后各分量的相关峭度

外圈故障声音信号经CEEMDAN和改进方法处理后，所得各分量的相关峭度如表3所示，分析峭度值最大的分量的时域波形和频谱图如图12，图13所示.通过对比，可知改进方法根据峭度指标有效提取出了包含故障冲击成分的模态分量IMF8.IMF8的时域波形图中周期性冲击明显，且通过IMF8的频谱图清晰地提取出了故障特征频率29.3Hz，特征频率倍频亦被有效提取，故可以有效判定故障类型为轴承外圈故障.实验结果再一次证明了本文所提方法的有效性.

图12 外圈信号经CEEMDAN处理后IMF6的时域波形和包络谱Fig.12 Time domain waveform and envelope spectrum of outer ring signal’s IMF6 processed by CEEMDAN

图13 外圈信号经改进方法处理后IMF8的时域波形和包络谱Fig.13 Time domain waveform and envelope spectrum of inner ring signal’s IMF8 processed by the improved method

4 结 语

本文提出的声音信号特征增强方法能对实测复杂轴承故障声音信号进行特征增强后继而实现信号分解，然后根据峭度最大值原则选取其中峭度值最大的模态分量，最终利用包络分析法提取轴承故障特征频率，从而通过声音信号实现轴承的故障诊断.该方法为挑选合适分量提供了较为理想的筛选指标.通过对仿真和实验信号的分析，可得如下结论：

(1) CEEMDAN方法可以有效去除声音信号中的多源干扰分量，从而更加准确地进行故障诊断.

(2) MCKD可以有效突出冲击成分.在声音信号故障诊断中，若特征故障频率被噪声淹没，采用MCKD可以在一定程度上减少因为分量选择不当而造成的误差.

(3) 在选取最优分量过程中，CEEMDAN与MCKD结合使用可获得更好的效果.本文所提的方法在一定程度上增强了冲击成分，为选择合适分量提供了一定的依据，研究结果为今后进一步研究自适应CEEMDAN方法奠定了基础.