基于动态规划的自适应和弦编配算法研究
邓 阳,周 莉,许 多,岳诚成,游梦琪,周蕊格
(1.中国地质大学(武汉) 艺术与传媒学院,武汉 430074; 2.同济大学 道路与交通工程教育部重点实验室,上海 201804; 3.伦敦大学学院 全球繁荣研究所,英国伦敦 WC1E 6BT; 4.亚利桑那州立大学 赫伯格艺术与设计学院,美国坦佩 85281)
和弦编配是音乐创作中的一个重要的环节,它对加强旋律的感情色彩,增强音乐作品的表现力有着重要的意义.传统作曲中的和弦编配主要采用耗时较长的人工完成.由于和弦编配可以看作是一个多阶段决策的过程,本文提出一种基于动态规划的自适应和弦编配算法,以推动现代算法作曲技术的快速发展.
自20世纪60年代以来,许多启发式算法被开发出来,将规则与模拟自然现象的随机性相结合,这些算法被不同程度地运用到了音乐科技领域.这些技术包括: 动态规划(Dynamic Programing, DP)、模拟退火(Simulated Annealing, SA)、禁忌搜索(Tabu Search, TS)和进化算法(Evolutionary Algorithms, EA)等.
1966年Bellman[1]提出了动态规划方法,动态规划的核心是贝尔曼最优性原理.这个原理可以归结为一个基本的递推公式,求解多级决策问题时,从末端开始,到始端为止,逆向递推.该原理适用的范围十分广泛,例如离散系统、连续系统、线性系统、非线性系统、确定系统以及随机系统等.1983年,Kirkpatrick等[2]提出了模拟退火算法的创新思想,模拟退火算法是基于Monte-Carlo迭代求解策略的一种随机寻优算法,其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性.禁忌搜索算法早在1977年就被Glover[3]提出来.禁忌搜索算法从过去的搜索历史中总结经验和获取知识,避免“犯错误”,因此是一种智能优化算法.
遗传算法是一种基于自然选择和种群遗传机制的搜索算法,由4种启发式算法组成: 遗传算法、进化策略、进化规划和遗传规划.该理论由Holland[4]提出,后续Goldberg[5]将此算法进行了发展.各种算法都有各自的优势与不足,根据具体情况采用合适的算法将极大程度地提高问题的解决效率.
目前动态规划的运用在我国主要集中在工程领域,张化光等[6]对国内外自适应动态规划方法进行了比较详细的总结,并对这一研究领域仍需解决的问题和未来的发展方向作了进一步的展望.刘柏私等[7]将动态规划运用在配电网重构模型当中,通过算例说明该算法具有较强的工程实用性.音乐相关研究主要集中在对和弦的识别上.闫志勇等[8]提出一种基于瞬时频率提取音级轮廓(Pitch Class Profile, PCP)特征的改进算法,通过动态规划法提取信号的节拍信息,此改进算法的和弦识别率相比传统算法有一定的提升.孙佳音等[9]根据音乐认知心理学原理,提出一种基于人工神经网络(Artificial Neural Network, ANN)的和弦实时感知方法,此方法的识别率与相关领域先进方法的效果不相上下.秦媛媛[10]提出的基于听觉图像的和弦识别算法最高正确识别率为76.2%,比同样基于人耳听觉特性的梅尔频率倒谱系数(Mel-Frequency Cepstral Coefficients, MFCC)特征正确识别率高20.4%.Zong等[11]提出了一种新的和弦搜索优化算法,并通过一些例子证明了算法的可行性,但是在优化的方法上缺乏和弦体系的理论支持.
综上所述,我国音乐和弦的算法研究已有一定的积累,目前主要集中在和弦的识别上,鲜少有涉及到和弦编配算法的研究.针对以上问题,本文结合伊·斯波索宾的和声理论体系[12],将动态规划方法运用到音乐创作的和弦编配当中,提出和弦体系构造函数(Constructor Function of Chord System, CFCS),将音乐中的和弦逻辑公式化,进而与动态规划方法相结合,实现机器自动编配和弦,以此来推动算法与音乐作曲技法的协同发展.
1 模型描述
本文的研究范围主要为大调的三和弦功能体系,以乐句为主要实验对象,采用伊·斯波索宾和声理论体系下的和弦进行逻辑为优化目标,暂不涉及特殊和弦的编配及和弦的转位.
1.1 和弦功能体系
音乐是人类情感的一种艺术表达载体,构成音乐的信息是极其复杂的,通常主要由旋律和伴奏组成,其中和弦在伴奏中占据非常重要的地位,是伴奏编配的核心基础.和弦是音乐基本理论中的一个概念,指的是几个音按照一定的音程关系构成的一组音高逻辑.从和声学的观点来看,和弦之间存在着一种主三和弦倾向性,这个倾向性将各个和弦统一起来形成一种相互关联的体系,这个体系就是和弦的功能体系[12].
调式中每个和弦都承担着各自的功能,例如在C大调中以C为主音构成的大三和弦在这个调式中承担着主功能的作用.
图1所示为在C大调的基础上构建的一套和弦功能体系,这个体系分别包含主功能组(T功能组)、下属功能组(S功能组)、属功能组(D功能组),每个功能组中包含一个主三和弦(T,S,D)和两个副三和弦(SⅡ,TSⅥ,DTⅢ,DⅦ),每相邻功能组有一个重叠的和弦,重叠的和弦同时拥有两个和弦的功能.
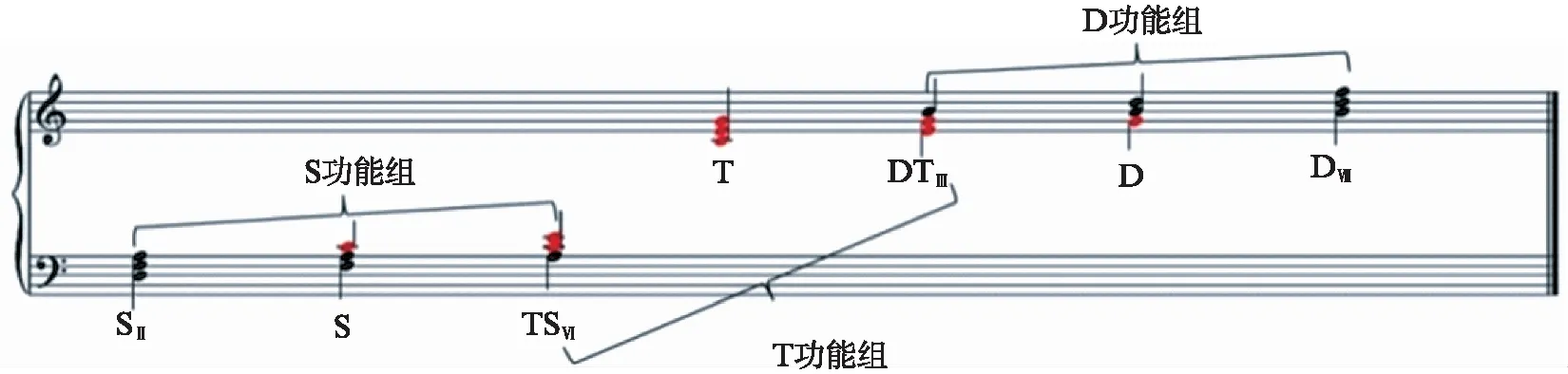
图1 三和弦的功能组Fig.1 Function group of triad
1.2 和弦进行逻辑
和弦的进行具有一定的逻辑.几个连续的和弦就构成了和弦进行.音乐作品的这种和弦进行可以在一定的节奏形式中,也可以脱离了前后的音乐,作为一个孤立的部分提出来.最简单的和弦进行以及其逻辑基础就是在主和弦之后引入一个或几个不稳定和弦,形成明显的紧张性,这种紧张再次进行到主和弦时得到解决.图2所示的是完全由主三和弦构成的和弦的基本进行逻辑,从一开始的主功能T进行到下属功能S,再进行到属功能D,最终终止在主功能T.
完全由主功能和弦构成的和弦进行相对单调,通常和弦进行中还会有副三和弦.图3所示为加入了副三和弦的和弦进行逻辑,在主三和弦的功能基础上扩展开副三和弦,相对于主功能和弦进行逻辑要丰富很多.本文主要基于以上和弦的进行逻辑展开研究与算法设计,暂不考虑特殊的和弦进行.
1.3 和弦编配模型的构建
音乐的和弦编配是一个有若干阶段的连续过程,基于动态规划的决策思路,利用计算机对和弦的编配路径进行搜索将极大提高作曲中和弦编配的效率,同时也可以极大程度地避免和弦编配中的不良进行.整个求解过程就是寻求一条最佳的和弦编配路径: 从起始点逐步计算最优函数,同时记录前驱路径,到达终点后回溯出最优的路径.

图2 和弦进行的基本方向Fig.2 The basic direction of chord progression

图3 补充副三和弦进行的基本方向Fig.3 The basic direction of chord progression of supplement secondary triad
动态规划的主要决策思路是把问题求解过程分解为若干个不同阶段问题的求解过程,其模型中的主要变量包括: 阶段变量、状态变量、决策变量[14].
阶段变量表示决策过程中的阶段数,每一次和弦选择都是一个决策阶段.和弦进行的前者与后者具有较大的关联,不同的和弦选择也将对应不同的指标函数.状态变量表示每个阶段开始面临的自然状况或客观条件.本文中,状态变量就是在每一个和弦选择时的若干选项,这些选项通过对每次可编配的调内和弦搜索获得.决策变量表示在某一个确定状态下的决策选择.当选择和弦功能的时候,前一个状态变量按照决策变量通过状态转移方程可得到后一个状态变量,每条路径选择将对应一个指标函数,通过从起始阶段到达终点后将可以获取一条全局最优决策路径.
在和弦的选择过程中,任何一个阶段的不恰当选择都有可能导致后阶段出现和弦的不良进行,本文目前仅基于一般和弦功能进行逻辑并以规避和弦不良进行和提高和弦丰富性为基本出发点来进行模型的构建.
2 算法设计
2.1 和弦体系构造函数(CFCS): FFOH(MAj,i)
音乐作品中每一个调都拥有特定的功能体系,这个功能体系决定了动态规划中每个阶段的状态Sk.定义变量和弦功能名称(Function of Harmony, FOH)用FOH表示,FOH∈{T,SⅡ,DTⅢ,S,D,TSⅥ,DⅦ},变量j表示每个调式的名称,分别对应12个自然大调,即j∈{C,C#,D,D#,E,F,F#,G,G#,A,A#,B}.MA(Musical Alphabet, MA)表示调名与12个自然大调的一种映射关系,MAj∈{0,1,2,…,11}.
三和弦分别由根、三、五音依次叠加构成,主三和弦由大三度(根音与三音相隔4个单位音高序号)加小三度(三音与五音两音相隔3个单位音高序号)叠加构成,副三和弦中除DⅦ和弦外都由小三度加大三度叠加构成,DⅦ和弦由两个小三度音程叠加构成.基于这种和弦构成逻辑联立调式音阶构造函数,按照和弦的音程关系,从而定义CFCS为FFOH(MAj,i):
(1)
式中: 音高变量N的下标r表示和弦根音(root);t表示和弦的三音(third);f表示和弦五音(fifth);变量i表示和弦在音高上所属的组别,i∈{0,1,2,…,10}.
例如基于C大调的和弦功能体系如下:
FT(MAC,i)={00,30,70,…,12710},
FSⅡ(MAC,i)={20,50,90,…,12510},
FDTⅢ(MAC,i)={40,70,110,…,12710},
FS(MAC,i)={60,100,130,…,12610},
FD(MAC,i)={70,110,140,…,12710},
FTSⅥ(MAC,i)={90,120,160,…,12010},
FDⅦ(MAC,i)={110,140,170,…,12510}.
2.2 自适应和弦功能选项搜索算法

图4 自适应和弦功能选项搜索算法的流程图Fig.4 Flow chart of adaptive chord function option search algorithm
为指定音乐的旋律声部编配和弦是给一个旋律配上合乎逻辑的、连续的和弦进行,所配和弦必须以对这个声部各个音的功能意义及它们的相互关系和发展的理解作为基础.在动态规划中,所有的阶段变量可通过自适应和弦匹配算法获取,具体算法流程如图4所示.
算法首先根据旋律所属调式,通过CFCS构建调式内和弦的功能体系,再通过遍历搜索所有调内和弦中是否包含待配和弦的旋律音高,进而构建出可编配和弦集合Sk,将Sk作为动态规划中的状态变量.
2.3 动态规划和弦编配算法
根据动态规划模型,把和弦编配的过程分为若干个相互联系的阶段,以便能按一定的次序求解,描述阶段的变量称为阶段变量.本文以每次和弦功能的选择的次数作为阶段数.
状态表示每个阶段开始所处的自然状况或客观条件,它既是该阶段重构组合的起点,又是前一阶段重构组合的终点.通常一个阶段有若干状态,第k阶段的状态就是第k阶段所有可编配和弦选项的集合,本文用Sk表示第k阶段的所有状态变量的总和,称为状态集合.
决策表示对某一阶段的可编配和弦的选择,用Uk表示第k阶段的决策变量,不同的阶段都要做出相应的决策,由每阶段的决策Uk(Xk)(k=1,2,…,n)组成的决策函数序列称为全过程策略,用Pk(Xk)表示,其中最优策略为Pk(Xk)*,即:
Pk(Xk)={U1(X1),U2(X2),…,Un(Xn)},
(2)
Pk(Xk)*={U1(X1)*,U2(X2)*,…,Un(Xn)*}.
(3)
给定第k阶段状态Sk,若该阶段的决策变量Uk一旦确定,则第k+1阶段的变量Sk+1也就完全确定,即
Sk+1=Tk(Sk,Uk).
(4)
通过CFCS可以获得调式内所有和弦的功能系统,只要单个和弦的功能集合包含待编配和弦的音符,则这个和弦将作为动态规划中的一个状态.例如为C大调作品配和弦,第1个待编配和弦的MIDI音高序号是60,而FT(MAC,i),FTSⅥ(MAC,i),FS(MAC,i)均包含60,则第1阶段的所有状态变量的集合为S1={T,TSⅥ,S}.
指标函数是用来衡量决策过程中某一决策序列(多次和弦进行序列的集合)优劣的一种数量指标,用Vk,n表示,即
Vk,n=Vk,n(Sk,Uk,Sk+1,Uk+1,…,Sn,Un,Sn+1).
(5)
根据和弦的进行逻辑,设和弦进行的基本方向集合Cb={TS,SD,DT},加入副三和弦后集合Cp={TTSⅥ,TSⅥS,SSⅡ,SⅡD,DDⅦ,DⅦT,DT,DTⅢT,DⅦTSⅥ,SⅡDTⅢ},同时考虑到和弦的丰富性,符合和弦的进行逻辑的和弦进行赋予较大指数,对于不符合和弦进行的和弦功能选择则赋予较小指数,指数越大表示越优.定义指标函数如下(k=0,1,…,n):
(6)
所有阶段指标函数的和为
(7)
指标函数的最优值称为最优函数,记为Fk(Sk),表示从第k阶段的状态Sk开始到第n阶段的终止状态的过程,采取最优策略所得到的指标函数值,即
Fk(Sk)=OPTVk,n(Sk,Uk,Sk+1,Uk+1,…,Sn,Un,Sn+1).
(8)
全局最优目标函数为
(9)
3 算例与实验
3.1 算例
本文根据柴可夫斯基《杜鹃》作品之八中的选段进行算例实验.样本谱例如图5所示,样本是一首G大调的作品,包括7个待编配和弦的音符.

图5 柴可夫斯基《杜鹃》作品之八中的选段谱例
Fig.5 The example of selected passages in 8 of Tchaikovsky’sCuckoo
通过CFCS,阶段数k∈{0,1,2,3,4,5,6},构建基于G大调的和弦功能系统FFOH(MAG,i),通过自适应和弦搜索算法可得到每个阶段的和弦备选集合Sk,S1={T,S,TSⅥ},S2={TSⅥ,S,SⅡ},S3={SⅡ,S,DⅦ},S4={SⅡ,DⅦ,D},S5={T,D,DTⅢ},S6={T,DTⅢ,TSⅥ},S7={T,S,TSⅥ}.
构建动态规划模型如图6(第398页)所示.
根据指标函数F(Vk)对所有的路径进行赋值,如图7(第398页)所示,通过动态规划方程求解,得到一条最优路径如图8(第398页)所示.

图6 动态规划状态变量模型Fig.6 The model for dynamic programming state variable
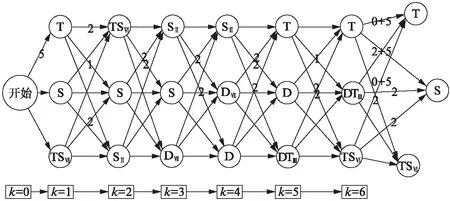
图7 动态规划指标函数F(Vk)模型Fig.7 The model for dynamic programming indicator function F(Vk)
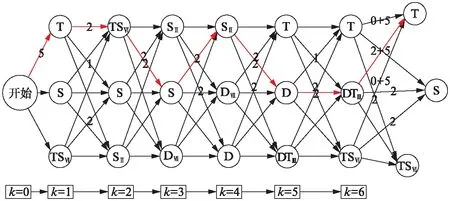
图8 最优求解图Fig.8 The diagram for optimal solution
图8所示模型分0~6共7个决策阶段,通过计算得出全局最优路径以红色实线标出.通过求解,最终得出一条最优路径P*,与作品本身的和弦编配完全一致,结果如下:
P*={T,TSⅥ,S,SⅡ,D,DTⅢ,T}.
所以,《杜鹃》作品之8中选段的和弦编配如图9所示.

图9 和弦编配图
Fig.9 The chart for chord arrangement
3.2 实验
本文选取伊·斯波索宾的《和声学教程》中的5个和弦编配样本(例18-245、例18-246、例20-267、例14-184、例17-233)对本算法进行了测试,测试结果如表1所示.

表1 算例实验的结果
尽管结果均不完全与标准示例一致,但由于和弦的编配本身是具有一定弹性的,无严格统一标准,并且实验结果与标准示例有较高重合率,故本实验总体结果为良好,实验证明本算法是有效可行的.
4 结 语
本文提出和弦体系构造函数(CFCS),将音乐中的和声学逻辑通过数学模型进行量化,通过设计一种自动和弦编配的动态规划算法,充分考虑和弦编配的逻辑性、连续性,将阶段变量、状态变量、决策变量、策略变量、指标函数等一系列动态规划指标完全渗入到音乐的和弦编配过程,最后通过对多个旋律样本开展自动和弦编配实验测试,评估结果显示本算法所自动编配的和弦具有良好的和声进行,是有效可行的.

