基于层次分析法和模糊综合评价的老年人建筑改造分析

邬樱 杨昌鸣

(北京工业大学 1建筑工程学院，北京 100124；2历史建筑保护北京市工程技术研究中心)

近现代建筑遗产不可避免与人类产生各种各样的关联，西方国家对待建筑遗产已经从被动式保护转变为主动适应。因为近现代建筑遗产具有使用价值，并不是孤立的“博物馆式保护”，所以在人们居住、利用、使用等实现建筑遗产使用价值的过程中，建筑会与人类相互影响。目前，对建筑改造的内容主要包括体量改变、功能改变和性能改变〔1，2〕。当前，全世界都在面对人口老龄化带来的挑战〔3，4〕。了解并满足老年人的需求是当今社会极为重要的课题。建筑对老年人的身心状况、行为模式等都会产生深远的影响。但是目前老年人对建筑的需求尚未得到足够的重视，建筑适老性相关的标准和规范体系也尚未完全建立起来。建筑评价是一项复杂的工作，涉及因素较多。同时，老年人的需求也呈现多样化，无法概括为某一项内容。现有对建筑的评价都是依托专家意见，或是仪器测量某些指标。而忽视使用者对于建筑需求的评价，尤其是从建筑利用、使用频率、与建筑联系紧密的使用者的需求角度对建筑进行评价。这种通过主观判断或是单一指标的评定是无法做到全面、科学地评判建筑。因此，本文基于老年人的需求，对老年人建筑改造进行分析，通过层次分析法和模糊综合评判的理论，提出科学、全面的评价方法，并依据评价结果提出相对应的改造策略，从而真正做到近现代建筑遗产改造的适老化设计、适老化改造、适老化更新等综合性适老性变革。

1 材料和方法

1.1层次分析法 层次分析法是一种结合了定性分析与定量分析的分析方法。它是由美国运筹学家A.L.Saaty所提出的，用来为选择最优方法提供依据。它适用于复杂的模糊综合评价系统,是目前一种被广泛应用的确定权重的方法〔5〕。层次分析法实现了对非定量事件科学的定性分析，同时还满足了精确的定量分析。本文首先采用层次分析法确定各层因子的权重，其步骤如下：

1.1.1建立应用层次分析法的结构模型 首先要把复杂的问题进行条理化、层次化，构建有递进关系的层次结构模型〔6〕。在这个模型中，可以分为目标层A、准则层B和方案层C，同一层的因素对下一层的某些因素具有支配作用，同时又受上一层次的某些因素支配。

1.1.2建立应用层次分析法的判断矩阵 为了比较指标层各因素对准则层的影响程度，对层次内的因素进行两两比较，得出各元素的权重，确定判断矩阵C=(Cij)n×n。本文中层次分析法采用1～9比例标度表示重要性的程度，见表1。

表1 1～9比例标度的含义

写作矩阵形式为：

(式1-1)

重要程度的赋值Cij由专家、学者或顾问酌定，减少主观方面的偏差。

补充说明，矩阵需满足完全一致性条件，即：

(1)对角线因素为1，即

Cij=1,i=j=1,2,…,n

(2)右上角和左下角对应因素需互为倒数，即

(3)元素具备优先次序的传递关系，即

1.1.3应用层次分析法进行单准则排序 对某个准则的各因素进行权重排序：

(1)将判断矩阵的元素按列进行归一化处理

(式1-2)

(2)所得到的C中元素按行相加：

(式1-3)

(3)对所得到的向量作归一化处理：

(式1-4)

得到的即为特征向量的近似解W=(W1,W2,W3,…,Wn,)T

(4)计算最大特征值λmax

(式1-5)

对于任意i=1,2,…,n,(BW)i为向量BW的第i个元素。

上述公式求得的权重是指由某一个评判人得出的结果，如果有多位评判人参与评价，需要采取算术平均的方法确定最终的权重。

1.1.4检验与修正判断矩阵的一致性 在实际的比较判断中，由于人类主观判断的差异性和客观事物的复杂性，因此需要检验和修正判断矩阵的一致性。具体步骤如下：

(1)计算偏离一致性指标CI

(式1-6)

式中n指判断矩阵的维数，λmax指最大特征值

(2)计算平均一致性指标RI

平均一致性指标，即同阶随机判断矩阵偏离一致性指标，由数理统计法得出，维数1～10，RI分别为：0.00，0.00，0.58，0.90，1.12，1.24，1.32，1.41，1.45，1.49。

(3)计算相对一致性指标CR

(式1-7)

计算所得的CR值必须符合CR≤0.1，CR值越小，表明判断矩阵的一致性越高；如果CR>0.1，需要重新修正，直到满足要求。

1.2模糊综合评价 模糊综合评价就是应用模糊变换原理和最大隶属度原则，考虑与被评价事物相关的各个因素，对其所做的综合评价〔7，8〕。模糊综合评价的步骤如下：

通过极差变换法，将每年影响生产设备采购量的相关数据均变为属于[0，1]区间的值。某生产设备各年采购量影响因素的相关数据经归一化处理的结果见表2。极差变换归一化处理并不改变各期数据之间的相对关系，因此，不会影响到采购量预测模型的构建。

(1)构建因素集

影响评价对象的所有因素组成的集合称为因素集，表示为U={u1,u2,u3,…,um}。等式左边表示因素集，等式右边表示具有不同程度模糊性的影响因素。

(2)构建评语集

评语集指评判者对评价对象所作评价等级的集合，表示为V={v1,v2,v3,…,vn}。等式左边表示评语集，等式右边表示各个评判等级。

(3)构建权重集

由于各因素的重要程度不同，为了反映各因素的重要程度，对各个因素ui(i=1,2,3,…m)赋予对应的权重Wi(i=1,2,3,…,n),权重集由各个权重组成的集合：

W={W1,W2,W3,…,Wn}

(式1-8)

一般来说，归一性和非负性条件是各权数Wi(i=1,2,3,…,n)应当满足的条件：

(式1-9)

可以把他们看作是每个因素ui对“重要”的附属程度。

(5)构建模糊关系矩阵

就一个因素单独出发，对因素集各元素的附属程度进行判定。设定ui为因素集中的第i个因素，rij是因素集中第j个因素vj的附属度。评判结果ui用模糊集合表示为：

(式1-10)

其中单因素评判集用 来表示是一个模糊子集：

Ri={ri1,ri2,ri3,…,rim}

(式1-11)

组成矩阵：

(式1-12)

(4)构建模糊综合评价

模糊综合评判就是对所有因素的影响进行考量，而不仅仅是一个因素的影响，基本的模型为：

B=W°R

(式1-13)

式(13)中，“°” 表示模糊运算。

最后，根据最大隶属度原则，得到所评价对象的评价等级：

(式1-14)

2 基于老年人的近现代建筑遗产二级模糊评价模型

老年人是相对较为特殊的群体，其社会角色、身体情况、心理状态随着年龄的增长在不断地发生变化。在经济社会的发展下，老年人的需求也已不再是简单的生理功能的满足，而是生理、心理、社会等多方面的需求。本文从老年人的需求角度出发，全面评价建筑的情况。这对促进老年人健康生活，进而推动和谐社会发展都具有重要的意义和价值。

2.1构建层次分析模型

2.1.1构建指标体系 依照指标选取的系统性、科学性、整体性、全面性、可比性、可操作性、开放性、可调整性的原则，综合相关研究成果〔9～15〕，并结合有关专家的征询和反馈意见，本文对影响老年人对建筑评价的因素进行了归纳分析，在此基础上建立基于老年人的近现代建筑遗产评价指标体系，见图1。

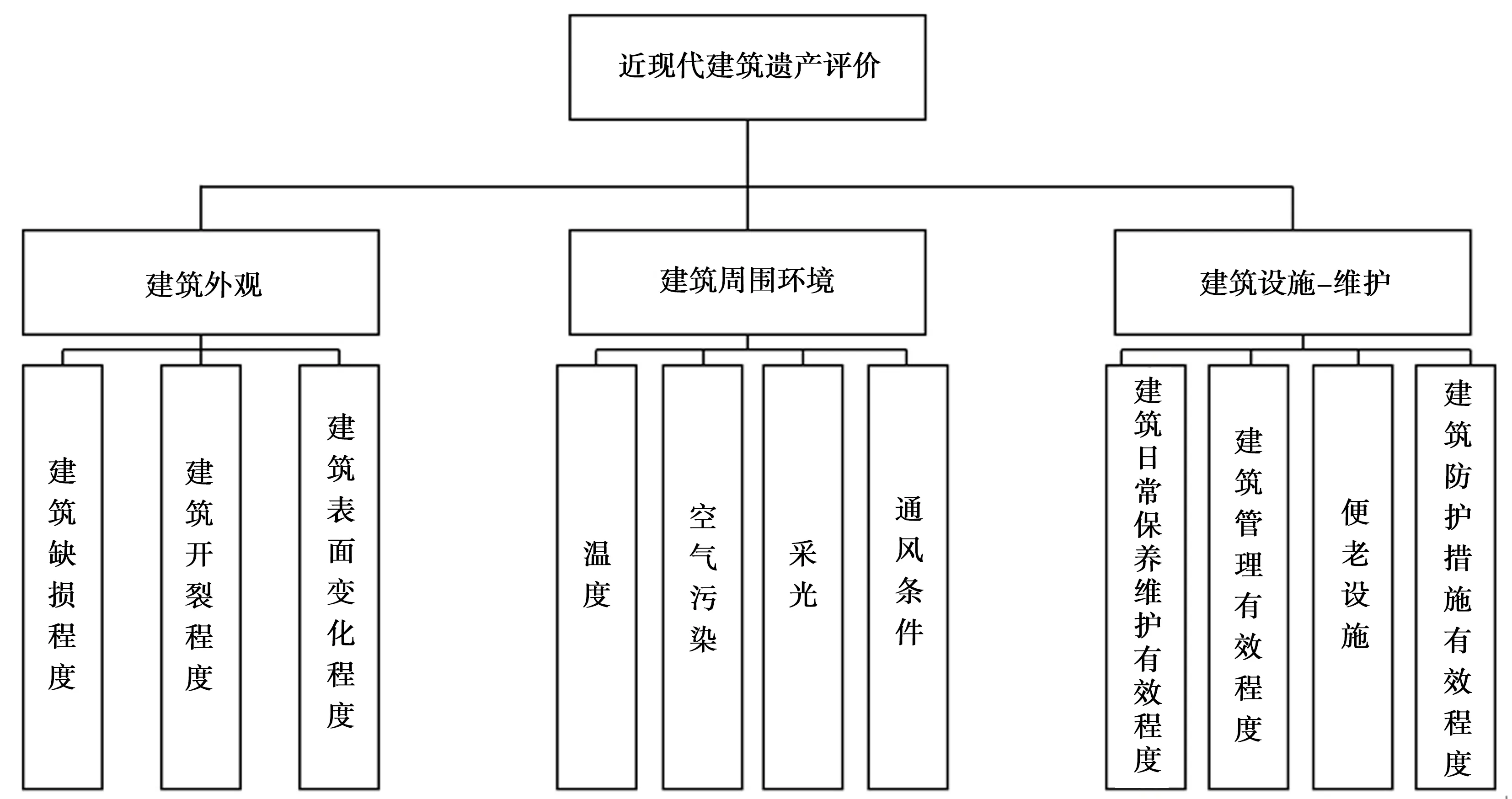
图1 基于老年人的近现代建筑遗产评价

2.1.2建立判断矩阵、单准则排序及检验与修正判断矩阵一致性 根据专家意见对老年人对建筑外观的需求、老年人对建筑周围环境的需求、老年人对建筑设施-维护的需求这三个因素的各项指标进行比较，建立判断矩阵，通过一致性检验结果后得到各要素指标的权重。

由上文中(式1-1)～(式1-7)计算所得：

w1=〔0.309 8,0.582 5,0.107 7〕

w2=〔0.363 6,0.363 6,0.207 1,0.065 7〕

w3=〔0.384 0,0.142 1,0.089 8,0.384 0〕

2.2构建模糊综合分析模型

2.2.1构建因素集 依据基于老年人的近现代建筑遗产评价层次分析模型，设立评价指标集U，一级评价指标为： U1(老年人对建筑外观的需求)、U2(老年人对建筑周围环境的需求)、U3(老年人对建筑设施-维护的需求)；二级评价指标为： u11(建筑缺损程度)、u12(建筑开裂程度)、u13(建筑表面变化程度)、u21(温度)、u22(空气污染)、u23(采光)、u24(通风条件)、U31(建筑日常保养维护有效程度)、U32(建筑管理有效程度)、u33(便老设施)、U34(建筑防护措施有效程度)。

2.2.2构建评语集 本文将基于老年人的近现代建筑遗产评价结果分为4个等级：优、良、中、差，V={优v1，良v2，中v3，差v4}。

2.2.3一级模糊评价 模糊评价根据模糊运算的不同，可分为Ⅰ型模糊评判和Ⅱ型模糊评判〔16〕。和Ⅰ型模糊相比，Ⅱ型模糊评判采用求积和加和的运算，是一种“加权平均型”的综合评判，信息损失量小〔17〕。由于本文所分析的因素较为复杂，在权重的分配上难以实现均衡，因此，本文的模糊综合评价采用二级模糊综合评判方法。二级模糊综合评判方法分为一级模糊评价和二级模糊评价。

(1)首先对每一因素进行单因素分析，由此得出该因素的矩阵为：

(式2-1)

(2)进行一级模糊评价：

Bi=wi°Ri

(式2-2)

(式2-2)中，“°” 表示模糊运算，根据本文的指标特性，采用 (·,∨) 型合成运算算子。

2.2.4二级模糊评价

(1)构建二级模糊评价的判断矩阵

在一级模糊评价的基础上，将每一个Ui看作是一个因素，用所得到的Bi作为单因素进行评价，构成二级模糊评价的判断矩阵：

(式2-3)

(2)计算权重向量

计算因素集U的s个子集的权重分配向量W={W1,W2,W3,…,Ws}

(3)进行二级模糊综合评价

B=Wi°R={B1,B2,B3,...,Bs}

(式2-4)

3 评价案例及分析

3.1评价案例

3.1.1北京宣武门教堂 宣武门教堂又称“南堂”，位于北京市西城区前门西大街141号，约建于1904年。它是北京天主教历史上第一座教堂，现在是北京教区主教座堂，其价值和地位是其他宗教类建筑所无法比拟的。1979年,宣武门教堂被列为北京市重点文物保护单位，1996年被列为全国重点文物保护单位。2017年12月2日，入选第二批中国20世纪建筑遗产名单。老年人因其特殊的身体情况和心理状况，容易感到孤独和恐惧，因此，宗教信仰成为老年人归属感的重要来源之一。随着宗教世俗化的发展，教堂已成为老年人群日常生活的重要活动场所之一。宣武门教堂作为北京重要的宗教活动场所，是与老年人活动密切相关的建筑。因此，本文选取北京宣武门教堂作为案例分析的对象。

3.1.2模型应用 选取北京宣武门教堂的80名老年人，使用基于老年人的近现代建筑遗产评价模型进行评价。

(1)确定各项指标的隶属度，建立指标集到评语集的模糊映射，分别确定矩阵为：

(2)一级模糊评价得到综合评价向量和矩阵：

B1=(0.158 0, 0.378 6, 0.081 6, 0.110 7)

B2=(0.963 6, 0.149 1, 0.040 0, 0.047 3)

B3=(0.095 0, 0.220 4, 0.098 8, 0.041 8)

(3)通过专家评估建立U的判断矩阵，通过一致性检验后得到：

W=〔0.637 0,0.104 7,0258〕

(4)二次模糊评价得到综合评价向量

B=(0.100 9, 0.241 2, 0.052 0, 0.070 5)。

基于老年人的北京宣武门教堂评价的最终结果为良。

3.2案例结果分析 通过使用本文的评价模型对北京宣武门教堂进行分析，得到基于老年人的北京宣武门教堂评价等级为良级，基本满足了老年人的需求。随机走访100位使用北京宣武门教堂的老年人(不含本文中选取的80名老年人)，得到的结论与本文评价方法的结果一致，证明本文评价方法有效、准确，可以满足要求。

4 讨 论

现有的建筑分析方法大多从设计者的角度出发，忽略了使用者的需求，特别是数量越来越庞大的老年人群的需求。同时，现有评价方法只能对单一因素进行分析，涉及多因素的分析时，无法科学进行评判。本文基于层次分析法、模糊综合评判的理论，采用基于层次分析法的二级模糊综合评判方法，在老年人的需求分析和建筑评价的特点上，提出基于老年人的近现代建筑遗产评价模型。该模型在实例验证下，证明其可行性和有效性。同时，该模型克服了传统一级模糊判断的弊端，实现了多目标、多因素问题的科学量化结果，有助于全面、准确地分析。通过本文的计算，得到基于老年人的北京宣武门教堂等级为良级，老年人对宣武门教堂的改造需求为一般性需求改造，老年人对宣武门教堂建筑外观的需求、对建筑设施-维护的需求在一定程度上得不到满足。老年人对宣武门教堂的改造需求主要集中在建筑表面变化、建筑开裂、空气污染、通风条件、建筑防护措施、便老设施的设置等几个方面。其中宣武门教堂建筑表面变化、建筑开裂、建筑防护措施等一般性需求改造属微生物劣化防治措施的范畴。宣武门教堂为地上1层砖木结构，三角木屋架，教堂南侧局部有2层，北侧钟楼局部有3层。室内木屋架为三角形木桁架。可根据老年人的一般性需求改造对宣武门教堂木质结构和砖墙结构分别实施微生物劣化的防治措施。醇酸、聚氨酯涂料可作为木质结构的预防性保护措施；三聚氰胺甲醛树脂MF法、环氧树脂修复法可作为木质结构的修缮性保护措施。有机硅化合物类、聚有机硅氧烷可作为砖墙结构的预防性保护措施；粒子喷射清洗法、超声波清洗法可作为砖墙结构的修缮性保护措施；同时，增加北京宣武门教堂的便老设施数量和种类，从而达到老年人对北京宣武门教堂建筑需求的改造。

老年人群是社会群体的重要组成之一，老年人对生活的满意度是衡量一个社会发展水平的重要指标，本研究从老年人的需求出发，将其作为建筑改造的出发点和落脚点，能够提升老年人的生活幸福感和满意度，对推进老龄社会发展、促进和谐社会稳定具有重要意义。