可证明安全的理性委托计算协议

田有亮，李秋贤，张铎,3，王琳杰

（1. 贵州大学计算机科学与技术学院，贵州 贵阳 550025；2. 贵州省公共大数据重点实验室，贵州 贵阳 550025；3. 贵州大学数学与统计学院，贵州 贵阳 550025）

1 引言

委托计算[1]是指计算能力相对较弱或资源受限的委托方将函数F的计算任务委托给不信任的计算方，计算方将返回一个计算结果及计算结果的正确性证明给委托方。委托方通过执行验证协议来验证返回结果的正确性，并且委托方验证该证明的工作量比计算函数F的开销要小得多，否则将失去委托计算的意义。委托计算一直受到学者的广泛研究，主要有基于复杂性理论构造方案和基于密码技术构造方案。基于复杂性理论构造方案主要应用的工具是交互式证明系统[2]、PCP（probabilistic checking of proofs）定理[3]等，Chung 等[4]在随机语言模型下对非交互式委托计算进行研究，给出了有效的解决方法。基于密码技术构造方案主要应用的工具有全同态加密[5]、基于属性加密[6]、混淆电路[7]等，Gennaro等[8]利用文献[7]的混淆电路构造了非交互式的委托计算方案，该方案有效地解决了基于计算理论方案的困难性问题。

理性委托计算属于理性密码学的研究范围，针对理性密码协议的研究领域，大多学者较多地关注利用博弈论方法来解决秘密共享、安全多方计算等问题，涉及理性委托计算的研究尚少。理性委托计算结合博弈论与委托计算的思想，协议中参与者都是理性的，而不是诚实的或是恶意的，且协议中通过效用函数来保证计算结果的正确性。传统的委托计算协议中，通常假设参与者要么是诚实的，要么是恶意的，但实际应用中，参与者大多是理性的，因此理性委托计算的研究成为当前的研究热点。Azar等[9]根据适当的评分规则，提出了一种理性证明系统，该系统中参与者既不是诚实的，也不是恶意的，而是理性的；随后Azar等[10]又利用Utility Gaps的思想构造了一种超有效的理性证明系统；Guo等[11]通过对理性证明系统的研究，解决了证明者计算能力受限的理性证明系统问题；Tian等[12]从理性的角度分析了安全通信问题，并提出了贝叶斯理性秘密共享方案；随后Chen等[13]从复杂性理论的角度研究了当存在多个证明者时，理性证明系统的理性证明问题。

关于理性委托计算的安全性问题是研究者最为关心的，如何利用效用函数构建安全可靠的理性委托计算协议更是当前的研究需求。Kilian等[14]提出了证明者使用 Merkle树向验证者发送对整个证明的短承诺的有效论证，证明者可以交互式地打开验证者的请求。Micali’s CS Proof[1]可以获得非交互式解决方案，该解决方案根据随机oracle应用承诺字符串来选择要打开的请求，消除涉及参数的交互。在最近的研究中，更多研究者较为关注非交互式协议，并且可以在标准模型中给予证明。

本文结合混淆电路和全同态加密技术提出了一种可证明安全的理性委托计算方案，该方案保证了所有理性参与者都得到最优的利益，保证委托计算输入和输出的隐私性。本文的具体工作如下。

1) 通过分析参与者的行为策略及参与者选择行为策略而得到的效用，设计了理性委托计算博弈模型。

2) 根据构建的委托计算博弈模型中纳什均衡需求，以及理性委托计算的安全需求，设计了可证明安全的理性委托计算安全模型。

3) 利用随机化混淆电路可重用的优点与全同态加密技术，保证了理性参与者结果的正确性及委托计算输入和输出隐私，从而构建了安全的理性委托计算协议。

4) 对协议的安全性与性能进行分析，证明了协议的安全性与输入输出隐私性，保证了所有参与者在协议中能获得利益的最大化即达到唯一纳什均衡。

2 基础知识

2.1 博弈论

定义1博弈。博弈表达的基本形式[15]由局中人集合P、策略空间S和效用函数u这3个要素组成，即G={P,S,u}，其中，P= {P1, …,Pn}，

S={S1,… ,Sn}，u= {u1,… ,un}。效用函数ui:S→R（R代表实数空间），表示第i(i=1,2,…,n)个局中人在不同组合下所得的效益。

定义2纳什均衡。对于博弈G={P,S,u}，如果由每个博弈方的一个策略所组成的策略组合中，任一博弈方Pi的策略都是应对其他博弈方策略组合的最佳策略，即对于所有的存在博弈对于任意sij∈S，则称为博弈G的一个纳什均衡。

2.2 全同态加密

全同态加密方案一般由以下4个阶段组成[16]。

加密阶段c←EncryptFHE(P KE,m)：输入公钥PKE和需要加密的消息m，利用加密算法输出一个对应的密文。

解密阶段m←DecryptFHE(S KE,c)：输入私钥SKE和需要解密的密文c，利用解密算法输出一个对应的明文。

运算函数cf←EvalFHE(P KE,ci,f)：输入公钥PKE，加密的密文组ci和需要求值的函数f，利用运算函数求解函数值。

其中，明文m= (m1,… ,mn)，密文c=(c1,…,cn)，密文组ci= (ci1,… ,cin)，函数值cf=f(ci)。

2.3 混淆电路

Yao的混淆电路[17]协议允许参与双方在不对明文做任何加密的情况下，对明文进行保密计算，该协议一般应用于半诚实参与者之间，是确保双方计算的通用方法。当应用在委托计算方案中时，委托方首先将委托的任意函数F转换为布尔电路C，然后将转换电路的混淆形式G(C)和委托方需要计算的函数x的混淆形式G(x)一起发送给计算方，这样代表该布尔电路的每条输入输出线的随机数均被加密。然后借助于准备阶段生成对应电路C的混淆表进行查表运算，通过计算布尔电路的每个门得到整个电路的输出。最后，计算方将计算结果的混淆形式G(F(x) )发送给对应的委托方，委托方根据混淆电路将计算结果转换为实际的输出y。

图1为混淆电路的结构，其中X和Y为输入线，Z为输出线。这3根导线分别对应有2个值：0和 1，即输入线的输入值和输出线的输出值。例如，当输入值a=0与b=1被选中后，混淆电路的任务就是需要安全地计算g(a,b)（g表示表 1中的输出线）的值。混淆电路表如表1所示。

由表1可知，每个输入输出线X、Y、Z，且每根导线制定2个随机值，对应于0和1。由表1可知，需要使用混淆电路表将联系起来，即在混淆电路表中，作为加密密钥，在合适的密钥输入下对进行加密，从而形成混淆电路。其中，当给定2个输入密钥时，混淆计算表只有一行是可以正确解密的，即这样可以有效地保证输入信息的隐秘性。

图1 混淆电路

表1 混淆电路表

在委托计算方案中，首先，委托方为每根导线选择2个随机密钥，因此委托方共具有6个密钥；其次，委托方对表1的每一行进行加密，形成混淆电路表；接着，委托方将混淆电路表进行重新随机排列，这样密钥的位置就不会显示与其有关联的值，保证了密钥的安全性。混淆电路表形成后，委托方将混淆电路表发送给计算方，以及输入计算值x和输入密钥由于计算方收到混淆电路表后，使用自己的密钥来解密混淆电路表，所以，委托方必须将密钥发给计算方。在此过程中，如果计算方将2个计算任务发送给委托方，那么计算方就可以解密更多信息，如果计算方要求委托方提供与其输入相对应的密钥，那么委托方就可以学习计算方的输入；为了避免信息的泄露，委托方与计算方使用不经意传输协议，使委托方获得与其在所有导线上的输入相关联的密钥，以保证输入输出的隐私性；最后，计算方计算电路，并将输出结果返回给委托方。

虽然混淆电路在委托计算方案中保护了客户端的输入输出隐私，但多次使用混淆电路进行计算时，恶意参与方可能将之前计算的标签输出作为本次的输出。结合全同态加密技术的混淆电路方法能够解决混淆电路的重用问题，委托方利用全同态加密技术为每次委托计算的输入选择一个新的密钥，以保证门电路信息不被泄露，从而解决了委托计算中混淆电路的重用问题。

2.4 可重用混淆电路

为解决混淆电路的重用问题，理性委托计算协议采用了随机化混淆电路技术，该技术主要利用全同态加密同态性质。可重用混淆电路方案中，密钥串s∈ { 0 ,1}l，需要使用的公钥是基于素数阶群q的元素向量；明文串x∈ { 0 ,1}n，其中，n=2l，l和n分别表示密钥串长度和明文串的长度，密文也是基于素数阶群q的多个元素向量。利用全同态加密的同态性质，通过群Zp上的 2个已知映射将0-1向量映射为同样长度的0-1向量。

将需要使用的混淆电路进行随机化处理，即在图1所示的布尔电路中，假设门电路g的第一根输入导线的2个标签为A0和A1，第二根输入导线的2个标签为B0和B1，输出导线的2个标签为C0和C1。为了实现随机化混淆，将每根导线随机化选择比特置换。假设将门电路g的第一根输入导线的2个标签A0和A1进行比特置换，其比特置换为θ和θ′，则输入导线新标签为θ(A0)和θ(A1)。根据全同态加密的密钥与明文的同态性质，随机选择h、h′∈ ( 0 ,1)l，则密文EAa(h)变换为Eθ(Aa)(θ′(h) )。继续选择随机数β∈ { 0 ,1}l，则形成的密文对为

由分析可知，通过为混淆电路的每根导线进行比特置换，实现重新随机化电路导线的标签和电路导线对应的密文对，从而实现随机化重复使用混淆电路的方法，且保证输入输出的隐私性。

2.5 理性委托计算

根据传统的委托计算定义，结合Yao的混淆电路与全同态加密技术，引出理性委托计算定义。假设理性委托方将计算函数F委托给理性计算方，理性计算方根据其博弈模型及效用返回计算结果。理性委托计算方案RD的形式化描述由以下4个算法构成。

1) K eyGen (F, 1λ)→ ( P K,SK)：将计算函数F用电路C来表示。根据Yao的混淆电路为每条导线随机选择2个值对于每个门电路g，计算其4个密文其中，公钥PK为全部的密文集，即私钥SK是其选择的导线值，即

2) P roGenSK(x) →σx：运行全同态加密算法，产生一个新的密钥对，(S K,PK )← Setup (1λ)。

EEFHE令wi⊂ S K 表示为输入x的二进制线值，且公共值为σx← (P KE,EncryptE( P KE,wi))，私有值为τx← S KE。

3) C omputePK(σx)→σy：计算Yao的混淆电路协议中的解密算法 D ecryptE(P KE,γi)，以获得正确输出线的标签，令σy为输出线的标签。

4) R ecoverSK(σy) →y∪ ⊥：使用公钥SK将输出线标签σy中的导线值映射到输出结果y的二进制表示形式上。如果映射失败，将输出⊥，并令计算方接受相应的惩罚。

定义3 正确性。如果问题生成算法生成的值使理性计算方输出正确的值，则理性委托计算协议RD是正确的，其形式化表示如下。

对于任意x∈Domain(F)，如果 K eyGen(F,1λ)→(PK,SK)，ProGenSK(x)→σx和 C omputePK(σx)→σy都成立，且以不可忽略的概率使 R ecoverSK(σy)→(y=F(x) ,1)成立，则理性委托计算协议RD是正确的。

在协议中，若对于所有的概率多项式时间，敌手A不能使委托方接受一个不正确的输出，则理性委托计算协议RD是安全的。

定义4 隐私性。理性委托计算协议RD的输入输出是隐私的，为理性委托计算协议RD定义敌手A，在协议中的优势为

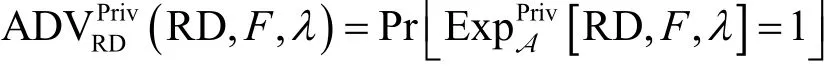
在协议中，若对于任意的函数F和所有的概率

多项式时间敌手A，概率是可以忽略不计的，则理性委托计算协议RD是隐私的，其形式化分析如下

即如果存在2个不相同的输入，产生的2个输出结果以可忽略的概率区分，则理性委托计算协议RD是隐私的。

3 博弈分析及其安全模型

3.1 博弈模型分析

理性委托计算是将博弈论与委托计算结合的新型的委托计算方案，通过引入理性参与者，使用效用函数来保证计算结果的正确性。一般来说，在委托计算方案中，存在3种类型的计算方：诚实的计算方，诚实的计算方会完全按照委托方的要求进行计算，并返回正确的结果；理性的计算方，理性计算方正确执行计算任务的效用必须大于执行其他任务的效用，如果在计算过程中懒惰计算的效用大于诚实计算，则理性计算方会选择懒惰计算；恶意的计算方，恶意计算方将试图破坏委托计算协议，并返回一个不正确的结果。实际上，由于协议中的参与者大多都是理性的，无论参与者是诚实或恶意的，在现实的协议中都是不合理的，因此，本文对理性的参与者进行分析。

假设存在理性委托方1P和理性计算方2P，理性委托方有计算任务F，其计算任务的本身价值为Re。此时，理性计算方有“诚实”地返回正确结果和“恶意”地返回错误结果这2种策略，即理性计算方P2的策略集为{诚实,恶意}。当理性计算方诚实地计算委托任务，其计算任务的成本为c( 1)，效用为u( 1)，返回正确答案后得到奖励为r，且奖励大于计算成本，即r＞c( 1)；若理性计算方存在恶意行为，则计算成本为c(q)，效用为u(q)，其中q为理性计算方作弊的概率，且u( 1)＞u(q)。

由于参与者都是理性的，此时理性委托方将根据理性计算方返回的计算结果选择“奖励”诚实的理性计算方或者“惩罚”恶意的理性计算方，即理性委托方1P的策略集为{惩罚, 不惩罚}。但当理性委托方未按照约定对理性计算方进行奖励，理性计算方可向可信第三方提出申诉，并对理性委托方进行罚款，记该罚款为Q1；同理，理性计算方存在恶意行为返回不正确的答案，理性委托方将对其进行惩罚，记该罚款为Q2。

基于对博弈模型的分析，可以得到理性参与者的效用矩阵。根据理性计算方的行为策略和理性委托方的行为策略，可以得到相应的效用矩阵，如表2所示。

表2 理性委托计算参与者的效用矩阵

根据理性参与者的行为策略分析，理性委托计算可以分为3个阶段进行。

1) 理性委托方1P对于计算任务F，可以选择自己计算，或者选择委托给计算能力强大的服务器，即理性计算方2P进行计算。

2) 理性计算方2P对于计算任务F，从策略集{诚实, 恶意}中选择一种策略进行反馈。

3) 理性委托方1P根据理性计算方2P反馈的结果，从策略集{惩罚, 不惩罚}中选择一种策略进行反馈。

将博弈论引入本协议中，利用子博弈精炼纳什均衡来分析理性委托计算。在每个阶段中，对应的参与方都有行为策略进行对应，例如，理性计算方2P“恶意”地返回错误结果，则理性委托方1P会选择惩罚理性计算方2P，即该策略组合可以达到纳什均衡状态，其理性委托方与理性计算方的策略与效用用博弈树来表示，如图2和图3所示。

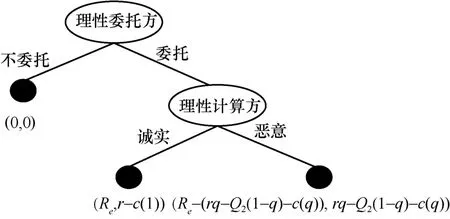
图2 理性计算方的效用博弈树

图3 理性委托方的效用博弈树

3.2 安全模型

根据上述的博弈分析，给出了基于全同态加密与随机化混淆电路相结合的理性委托计算安全模型。对真实实验中与理想实验中输出结果进行分析，如果任意概率多项式时间的区分器不能区分这 2个实验结果，则本实验是安全的，满足语义安全。此安全模型用于抵御恶意敌手的多项式次查询，保证委托计算输入输出的隐私性及委托计算结果的正确性。

1) 理性委托计算理想实验下的安全模型

理想实验挑战者与仿真器S。

初始化阶段挑战者将安全参数1λ发送给仿真器。

挑战阶段敌手向挑战者发送有效的明文概率分布wi，挑战者根据概率分布wi随机选择 2个明文wi0和wi1。

解密阶段仿真器随机选择b∈ { 0 ,1}，将其发送给挑战者。挑战者打开对应的明文分量得到(wi)i∈b，然后将明文分量发送给仿真器。

输出阶段仿真器调用解密算法σy←DecryptE(P KE,wi)得到解密结果，并输出解密结果σy。

2) 理性委托计算真实实验下的安全模型

真实实验挑战者与敌手。

初始化阶段挑战者调用密钥生成算法KeyGen( 1λ,F)→ ( P K,SK)得到公钥私钥对，并将公钥PK发送给敌手。

解密阶段1 敌手查询密文γi，挑战者调用解密算法 D ecryptE(P KE,γi)进行回复。

挑战阶段敌手向挑战者提交 2个长度相同的明文消息w0和w1，挑战者随机选择一个比特b，其中b∈ { 0,1}，调用加密算法加密wb，从而得到挑战密文。挑战者将得到的挑战密文发送给敌手。

解密阶段2 敌手查询密文σx，其中σx≠σx∗。挑战者继续调用解密算法σy←DecryptE(P KE,wi)得到解密结果σy。

输出阶段挑战者将结果yσ发送给敌手，敌手猜测b的值b′。

若敌手猜出bb′= ，则敌手赢得本次比赛。

4 理性委托计算方案构造

本节结合混淆电路与全同态加密技术，设计可重用的理性委托计算协议。在协议中，假设理性委托方P1将需要计算的函数F秘密地发送给理性计算方P2，只有当理性参与者发送正确的结果，才能使自己得到的效用最大；若理性参与者存在欺骗行为，则会受到远大于计算成本的惩罚。方案中λ为安全参数，执行计算函数F任务所需时间为t，具体如下。

初始化阶段

首先，理性委托方P1将计算函数F转换为布尔电路C，并生成混淆电路G(C)。根据Yao的混淆电路的构造，为每个电路导线wi随机选择 2个值，对于每个门电路g，计算其4个密文。每个门电路的公钥PK为密文组集合，即，私钥SK是其选择的导线值，即

然后，协议将执行全同态加密算法，首先由密钥生成算法生成一个新的密钥对(S KE, PKE)。在此过程中将随机选择的导线wi表示为输入x的二进制线值。利用全同态加密的密钥对将输入线值进行编码，其公有编码值为σx←(PKE,EncryptE(PKE,wi))。

最后，理性委托方P1把混淆电路G(C)和输入x的编码一起发送给接受计算任务的理性计算方P2，以便理性计算方在没有理性委托方存在的情况下获得G(x)关于x的任何信息，从而保证输入的安全性。

委托计算阶段

理性计算方P2接收到计算任务后，根据输入导线w、w′、γ和输出导线Dw(Dw′(γ))构建电路Δ，其中Dw为Yao的混淆电路中加密算法E对应的解密算法。根据Yao的混淆电路，计算方解析收到的输入编码σx。由解密算法DecryptE(PKE,γi)得到布尔电路正确的输出线的标签σy。其中σy←DecryptE为二进制中表示y=F(x)的线值。理性计算方将得到的计算结果作为输出返还给理性委托方P1。

支付效用阶段

理性委托方P1接收到计算结果σy后，首先利用同态加密算法的私钥SKE解密σy←EncryptE来获得然后使用公钥SK将输出线标签σy中的导线值映射到输出结果y的二进制表示形式上。

如果y=F(x)，理性委托方P1需根据约定在时间t内将奖励金r支付给理性计算方P2，此时理性委托方的效用为Re-r，理性计算方的效用为r-c( 1)。

如果映射失败，即y≠F(x)，理性委托方P1将会对理性计算方P2进行惩罚，罚金为Q2。此时理性委托方的效用为Re- (rq-Q2(1 -q) -c(q))，理性计算方的效用为rq-Q2(1-q) -c(q)。

由博弈分析可知，只有当理性委托方和理性计算方都选择诚实的行为策略时，他们的效益才最大，此时该策略组合也可以达到纳什均衡。

5 安全性分析

定理1 在 DDH（decision Diffie-Hellman）假设下，本文所提的理性委托计算协议是语义安全的。

证明本文所提理性委托计算协议是在 DDH假设下，以全同态加密与随机化混淆电路技术为基础的。在分析其安全性时，如果2次输入执行的猜测结果是以不可忽略的概率分辨的，则定理的结果成立。

假设存在概率多项式时间（PPT, probabilistic polynomial time）敌手A，其安全参数为λ，有不可忽略的δ，且

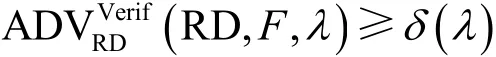
在协议中，定义L为敌手A执行查询的上限。且在理性委托计算的过程中，随机化混淆电路的门电路会随机生成，因此敌手A不能因为多次执行查询而学习标签的相关情况，如果敌手A在游戏中获得胜利，则必须是一次性查询就获得成功。

假设敌手A在第i次执行时获得成功，其中，1≤i≤L，则Hi(R D,F,λ)=1；如果执行失败，A则表示为

在协议执行过程中，如果敌手A在第i+1次执行时获得成功，则敌手A猜测的计算输入为Ai+1；如果执行失败，敌手A猜测的计算输入为Ai。因此敌手A在2次实验过程中有可忽略的概率区分，具体如下。

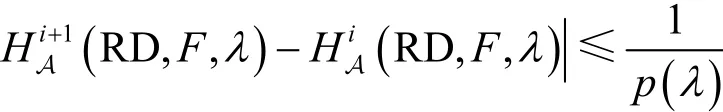
其中，p是一个多项式，且对任意多项式时间敌手A有

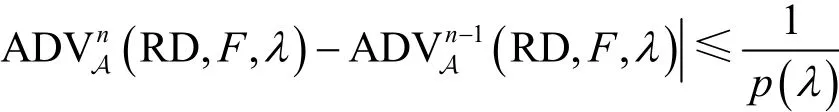
在上述的实验中的优势为

在协议中，若对于所有的概率多项式时间敌手A，概率 A DVVerif(R D,F,λ)是可以忽略不计的，

RD则理性委托计算协议RD是安全的，即敌手A在2次实验中以可以忽略的概率区分 2次猜测结果，因此，上述理性委托计算协议是语义安全的。在存在恶意参与方的情况下，理性计算方无法获得关于输入w和输出σy的任何信息，则可以保证委托方的输入输出隐私。

证毕。

定理2 根据设计的理性委托计算协议，当理性参与者都选择诚实策略时，协议可以满足纳什均衡状态，即全局可以达到效益最优。

证明在协议的初始化阶段，如果理性委托方P1和理性计算方P2都遵守协议规则，双方将会选择最有利的行为策略。理性计算方P2在其计算能力范围内接受理性委托方P1发送的计算任务G(C)和输入x。

在委托计算阶段，理性计算方P2在时间t内将计算结果σy← D ecryptE(P KE,wi)作为计算输出发送给理性委托方P1。此时需要考虑理性参与者选择的行为策略，若理性委托方与理性计算方都采取诚实策略，理性委托方就可得到R-r的效用，理性计算方也可得到r-c( 1)的效用；若理性委托方选择诚实策略，按时将奖励金返回给理性计算方，而理性计算方选择恶意策略，理性委托方就可得到Re- (rq-Q2(1 -q) -c(q))的效用，理性计算方也可得到rq-Q2(1 -q) -c(q)的效用；若理性委托方选择恶意策略，没有将奖励金返回给计算方，而理性计算方选择诚实策略，理性委托方就可得到Re-Q1的效用，理性计算方也可得到r-c( 1)+Q1的效用；如果理性委托方和计算方都选择恶意策略欺骗对方，理性委托方就可得到Re-Q1的效用，理性计算方也可得到rq-Q2(1 -q) -c(q)的效用。

在支付效用阶段，由于在博弈模型中奖励金大于计算成本，即r＞c( 1)，且其效用有u( 1)＞u(q)，罚金Q1与Q2也远大于计算成本。所以只有当理性参与方都选择诚实的策略时，理性委托方P1和理性计算方P2才能得到最大的效用，此时全局状态也达到最优。

证毕。

根据协议的分析可知，用子博弈精炼纳什均衡来分析理性委托计算，只有当理性参与方都选择诚实策略时，全局才可以达到最优状态，执行协议结束，即该协议具有正确性，且满足纳什均衡状态。

6 仿真实验与性能分析

6.1 仿真实验

针对本文所提的可证明安全的理性委托计算协议，将不同数量的模指数运算委托出去后引入本模型中，使用本文所提理性委托计算协议，理性委托方不需要对返回结果进行验证，委托计算所需时间对比如图4所示。由图4可知，用户通过理性委托计算所消耗时间比直接计算和委托计算消耗时间都要少，并且当委托数量增大时，3种方式所需时间的差距也在增大，而理性委托计算的计算效率也更高。

图4 委托计算不同模型的时间开销

6.2 性能分析

本文提出的理性委托计算协议与现有的委托计算协议进行比较，具体如表3所示。从委托计算的计算复杂度、通信复杂度、可证明安全等方面进行对比。其中，“√”表示满足该性能，“×”表示不能满足性能。

Kupcu等[18]提出了一种理性的委托计算协议，该协议激励所有的理性计算方正确地执行委托任务，但不关心计算任务或数据的隐藏，只关心计算结果的正确性，其计算复杂度为O(1)，通信复杂度为1，未能满足可证明安全的性能。

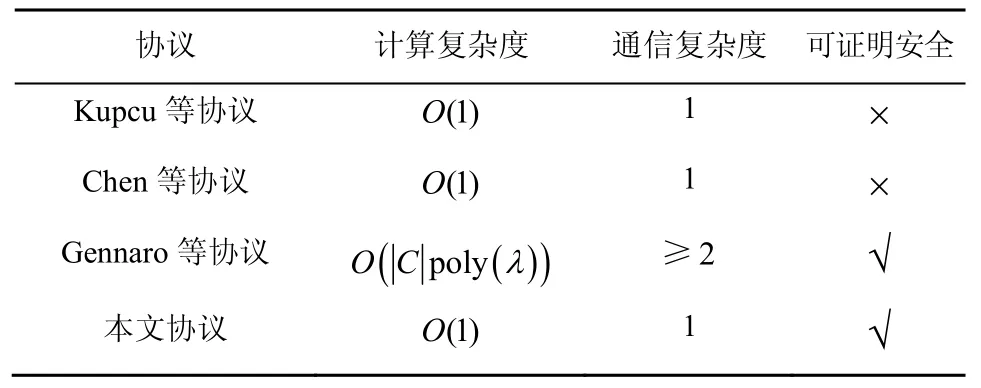
表3 本文协议与其他协议性能对比

Chen等[19]提出了在分布式环境中将计算任务委托给不受信任的计算方，利用新的公平有条件支付方案解决委托方与不诚实的计算方之间的信任问题。该协议的计算复杂度为O(1)，通信复杂度为1。但该方案未能对安全性进行有效的证明，未能满足可证明安全的性能。

Gennaro等[20]提出了基于Yao的混淆电路与全同态加密技术构造可验证的委托计算协议，该协议虽然将计算任务委托给不受信任的计算方，但能保证参与者输入和输出的隐私。该协议虽然满足了可证明安全的性能，但由于方案中需要验证计算结果的正确性，所需的计算复杂度为通信复杂度至少为2，因此性能较低。

本文协议是基于 Yao的混淆电路技术和全同态加密技术构造的理性委托计算协议。在协议中构造委托计算博弈模型，取消了委托方对结果的验证过程，而是通过参与者的效用函数保证计算结果的正确性。只要参与者遵守协议，最终他们都能获得最大的收益，并能达到最终的纳什均衡状态。本文协议的计算复杂度为O(1)，通信复杂度为1，且满足可证明安全的性能。

7 结束语

本文引入了理性委托计算的概念，将计算任务委托给不受信任的服务器，并详细分析了在博弈论框架下委托计算中各参与方的效用及策略，设计了可证明安全的理性委托计算协议，该协议将Yao的混淆电路与全同态加密方案相结合，即使协议中存在恶意的敌手也能保证高效的委托。该协议也保证了委托方的输入输出隐私安全，以及输出结果的正确性。本文是基于Yao的混淆电路与全同态加密方案设计了可证明安全的理性委托计算协议，而将计算任务委托给比全同态加密更有效的委托计算方案中，这将是下一步要研究的工作。