基于Python的圆锥滚子轴承滚子修形软件开发

张军飞，郭玉飞，李震

(1.大连理工大学 机械工程学院，辽宁 大连 116024；2.瓦房店轴承集团有限公司，辽宁 瓦房店 116300)

圆锥滚子轴承具有承载能力大，可同时承受径向和轴向联合载荷以及长寿命等性能，被广泛应用于汽车、机床、机车、轧机等机械行业[1-3]。滚子与滚道接触属于有限长线接触，由于滚道在滚子两端的外侧处于凹陷状态会引起边缘应力集中，导致滚子与滚道接触应力过大，从而过早失效[4]。为减小边缘效应，需对滚子或滚道素线进行修形。文献[5]分析了直线型、圆弧型和对数型修形圆锥滚子的接触应力，并对轴承疲劳寿命进行了分析；文献[6]分析了在不同修形素线下圆锥滚子的刚度、位移及接触应力分布情况；文献[7]分析了圆锥滚子处于偏斜时的接触应力分布情况；文献[8]分析了圆锥滚子与滚道接触力的数值求解方法。目前，圆锥滚子修形基础理论与接触问题研究较多，修形滚子接触应力大多通过有限元进行计算，建模复杂，计算时间长[9]。鉴于此，以某型号圆锥滚子轴承为研究对象，基于接触应力计算模型开发了滚子修形软件，用于滚子修形设计及接触应力快速计算。

1 圆锥滚子轴承接触应力计算模型

滚子与滚道间的接触问题可应用Hertz线接触理论进行求解，而线接触理论只适用于无限长柱体间的接触，圆锥滚子轴承中滚子的长度有限且小于滚道宽度，属于非Hertz接触问题，一般采用数值计算方法进行接触应力求解。将滚子和滚道看作2个弹性体，在径向载荷Q作用下发生弹性变形，并形成接触区域Ω。滚子与滚道接触的变形协调关系如图1所示，接触区域如图2所示。

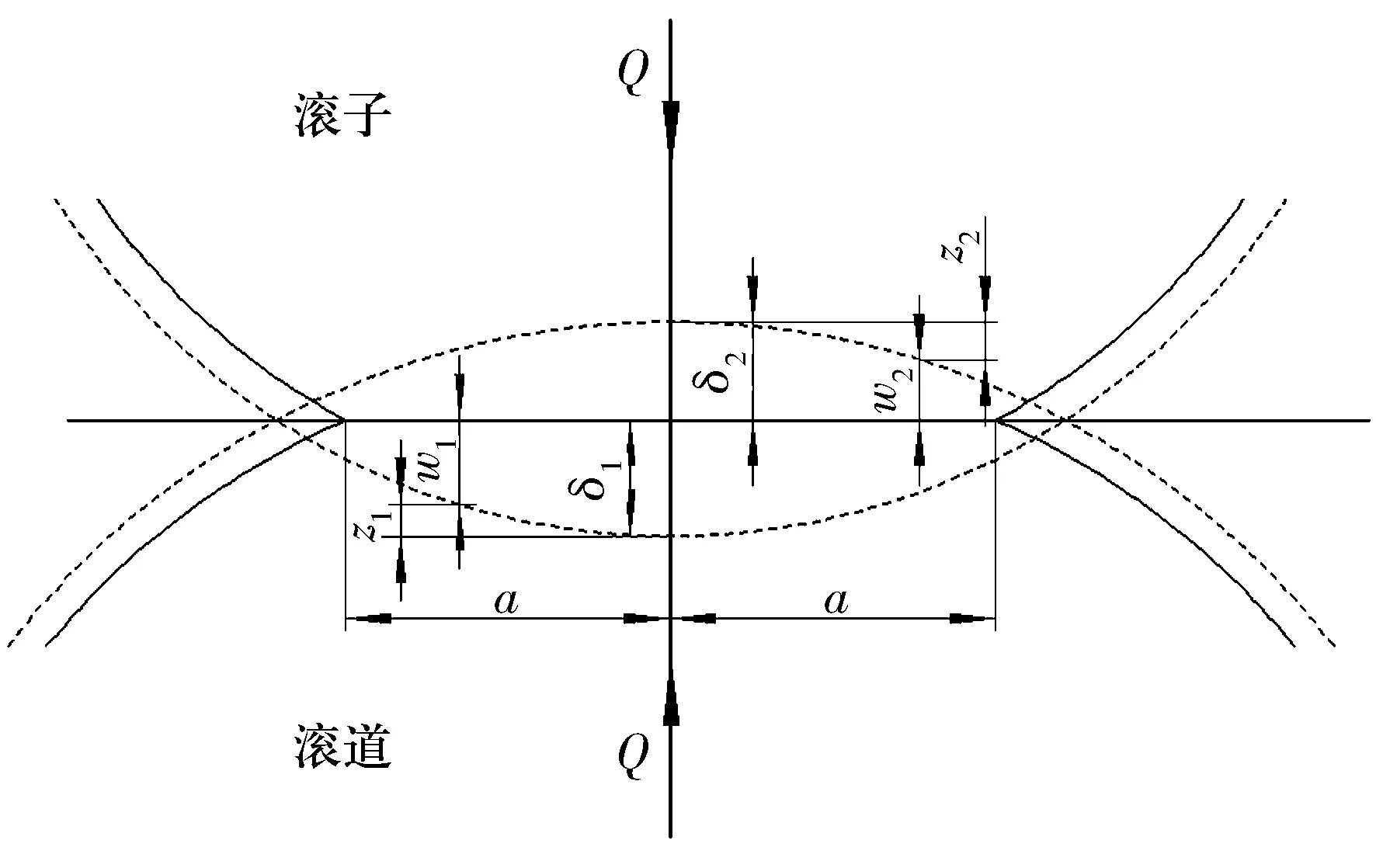
图1 滚子与滚道接触的变形协调关系

图2 滚子与滚道的接触示意图

设滚子与滚道的弹性趋近量为δ，则

δ=δ1+δ2=w1+w2+z1+z2，

(1)

滚子与滚道的接触变形为[10]58

w(x,y)=w1+w2=

，(2)

(3)

式中：w1，w2分别为滚子和滚道在接触点的弹性变形量；z1，z2分别为未变形前滚子表面与滚道表面对应点到初始接触点的垂直距离；E1，E2分别为滚子与内圈的弹性模量；ν1，ν2分别为滚子与内圈的泊松比；p(x′,y′)为接触区内点(x′,y′)的接触应力。

滚子受力平衡条件为

(4)

设接触区域长度为滚子有效接触长度Lwe，接触区域半宽初值为a0。滚子在垂直于素线方向上的截面是大小不同的椭圆，Zk为修形曲线上k点距滚道表面的垂直距离，Lk为k点与滚子小端距离，接触点曲率半径为[10]62

Rk=0.5Dk/cosθ，

(5)

Dk=(1-Lk/Lw)d+(Lk/Lw)D，

(6)

式中：d为滚子小端直径；D为滚子大端直径；θ为滚子半锥角；Lw为滚子公称长度。

从位置1移动到位置2，弹性趋近量与接触半宽关系如图3所示，接触半宽初值a0为

图3 δ-a0关系示意图

(7)

将接触区域划分为m×n个网格单元，假设每个单元内接触应力pj恒定，任意单元j的长半轴为aj，短半轴为bj。接触区域划分如图4所示，接触单元如图5所示。

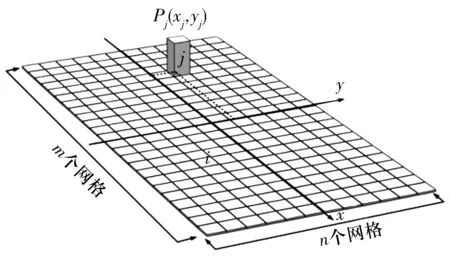
图4 接触区域划分示意图

图5 接触单元示意图

单元j区域内的接触应力对单元i中心点(xi，yi)处产生的弹性变形为

(8)

柔性系数为

(9)

弹性趋近量初始值为

(10)

通过求解方程组计算出每个单元上的接触应力，在计算迭代过程中得到接触应力为负值的点表示此处单元未发生接触，应在下次迭代计算中排除这些单元，通过判断滚子受力平衡条件进行弹性趋近量δ的修正。接触应力计算流程图如图6所示。

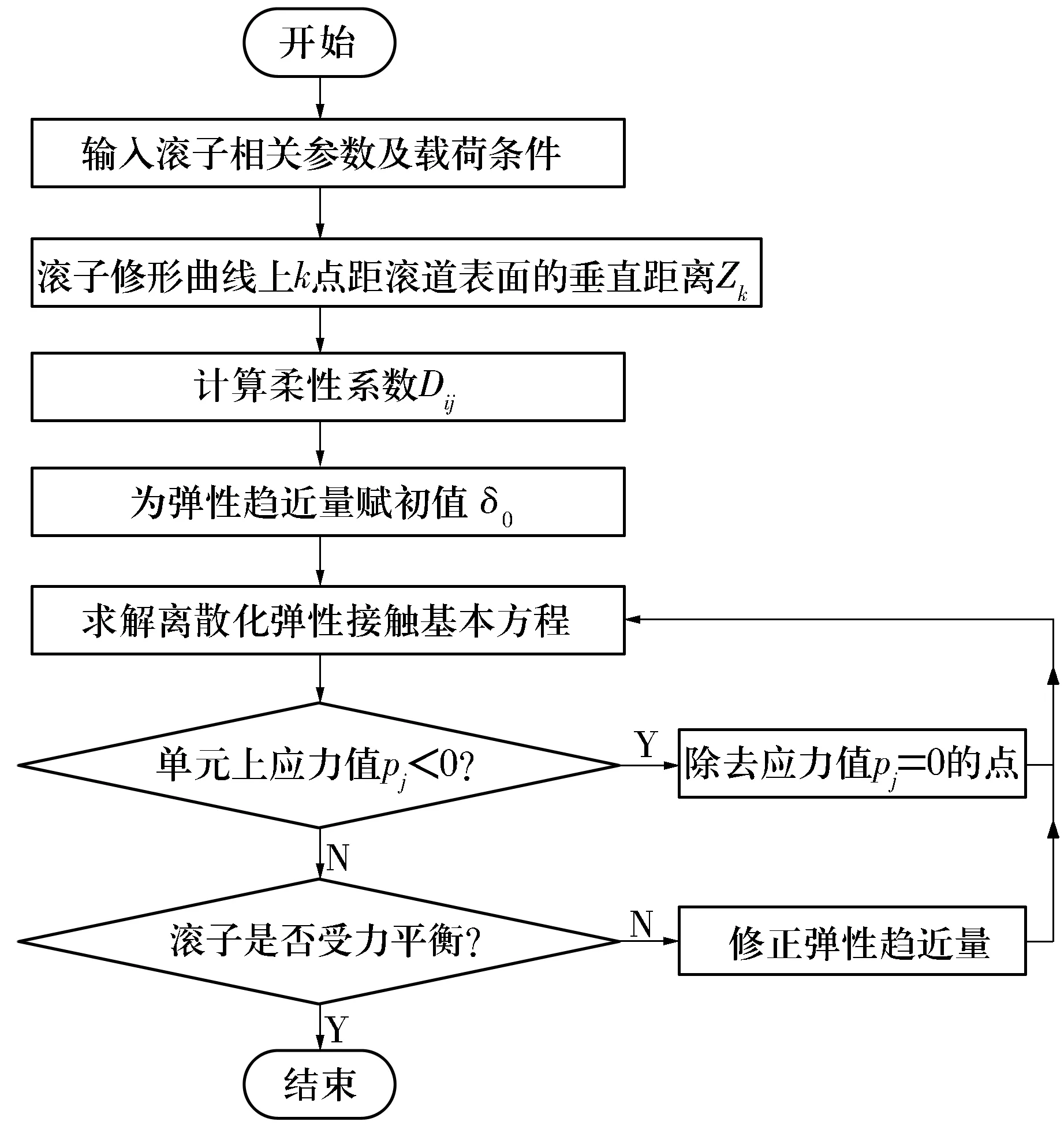
图6 接触应力求解流程图

圆弧修形滚子和对数修形滚子分别如图7、图8所示，圆弧修形曲线方程为

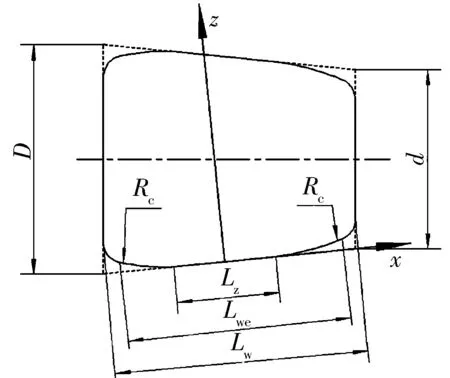
图7 圆弧修形滚子

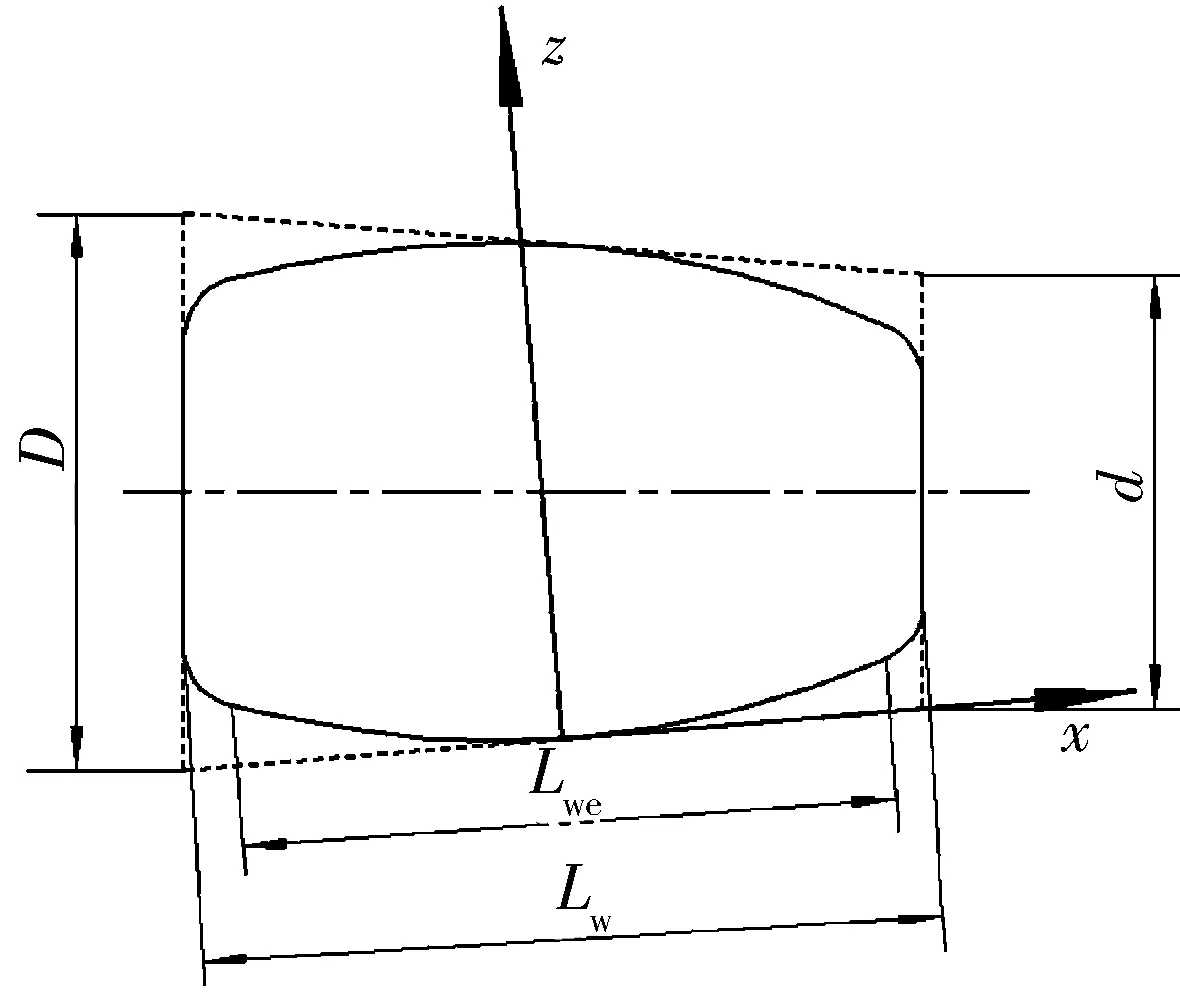
图8 对数修形滚子

,(11)

对数修形曲线方程为

(12)

式中：Rc为修形圆弧半径；Lz为滚子素线直线段长度。

2 滚子修形软件开发

为提高滚子修形设计工作效率，基于弹性接触力学模型及滚子修形设计理论，采用Python语言设计开发了滚子修形软件，可应用于圆柱和圆锥滚子的修形曲线设计。与有限元法相比，该软件能计算滚子在不同修形方式下的接触应力，并将计算数据进行可视化处理，利用该软件可以极大提高滚子修形设计效率。

2.1 软件开发工具

Python是一种面向对象的解释型高级计算机程序设计语言，语法简洁，可读性高，程序开发与维护难度低，具有众多丰富强大的模块，可大大提高开发效率。软件采用了Numpy，Scipy，Matplotlib等科学计算与绘图的扩充程序库。软件图形用户界面采用Tkinter模块实现，Tkinter是Python的标准Tk GUI工具包的接口，Tk和Tkinter可以在大多数的Unix平台下使用，同样可在Window和Macintosh系统中应用，系统兼容性较好。

2.2 软件开发与功能组成

滚子修形软件的模块主要包括滚子类型选择，滚子尺寸及材料参数、工况及修形参数输入，后台处理，计算结果存储和数据可视化，软件架构如图9所示。

图9 滚子修形分析软件架构图

在软件开发过程中，为了使程序结构模块化及便于后期维护修改等，将软件中各功能模块编写在主程序文件及多个不同的子程序文件中，主程序主要包括用户界面的建立，功能模块的调用，数据传入接口，通过在主程序中导入其他程序文件来实现各功能模块的调用及数据的传输与处理。

在软件主程序中利用Tkinter库中GUI相关功能开发了便于学习和使用的图形用户界面，采用参数化的操作方式对滚子结构及工况参数进行设定，用户输入的数据在计算过程中可自动传入计算处理模块进行数据处理及保存。软件可对圆柱滚子和圆锥滚子进行修形，提供直线型、圆弧型、对数型3种修形方式。不同的滚子类型和修形方式有其相对应的参数输入面板(图10)。

图10 滚子修形系统参数输入与数据可视化界面

软件的后台计算处理模块基于文中弹性接触力学及滚子修形理论进行开发。首先应用Sympy符号计算库进行了相关方程式的推导工作，程序中关于柔度系数、修形曲线方程、滚子与滚道表面间矩等物理量通过建立相应的函数进行调用计算。滚子受力平衡方程使用Numpy库中的linalg模块进行求解，并通过while循环对计算结果进行判断来对弹性趋近量进行修正，直到计算结果满足求解条件。

软件数据存储模块可将重要物理量参数以及计算处理结果进行存储和分类，保证数据安全以防止数据流失，并可供用户调用分析。软件可视化功能模块将Tkinter库中的显示功能与Matplotlib库中的绘图功能相结合使用，可将计算结果以图像方式展示在用户界面中，便于用户直观快速地分析问题。软件具体程序代码可参考网址进行查看[11]，读者只需下载安装Anaconda集成开发环境即可运行软件代码，软件工作流程图如图11所示。

图11 滚子修形软件工作流程图

3 实例分析

3.1 软件计算结果分析

以某型号圆锥滚子轴承为研究对象，主要参数见表1。轴承套圈与滚子材料为GCr15，弹性模量为207 GPa，泊松比为0.29。

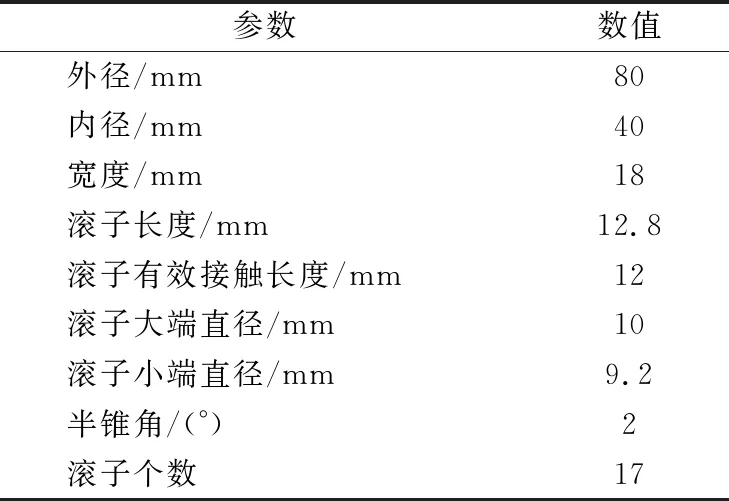
表1 圆锥滚子轴承主要结构参数

在外载荷Q为1 kN时滚子接触应力如图12所示。由图可知：1)直线型滚子端部出现明显应力集中现象，滚子中间段应力分布较均匀；2)圆弧型滚子应力峰值高于直线型和对数型滚子，这是由于圆弧型滚子接触面积小于另外2种滚子，圆弧型滚子应力分布较均匀，在圆弧与直线过渡处有微小边缘效应；3)对数滚子应力分布较均匀，无明显应力突变。

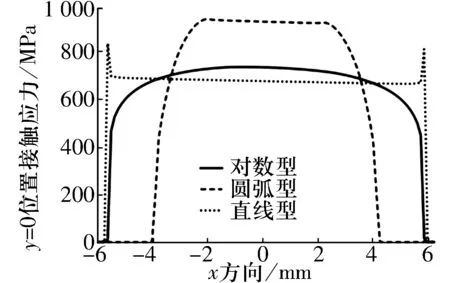
图12 Q=1 kN时滚子接触应力

在外载荷Q为1 kN时3种修形滚子与滚道接触区域(图2)应力分布如图13所示，由图可知：在接触区域两端应力曲线分布较为密集，滚子中部较为稀疏，由于滚子小端接触点曲率半径较小，滚子小端接触应力会略大于滚子大端。

图13 Q=1 kN时3种修形滚子接触应力分布

3.2 有限元仿真分析

为验证软件分析的合理性，基于ANSYS分析了对数修形滚子的接触应力分布情况，其有限元仿真与软件分析结果对比如图14所示。由图可知：最大接触应力误差在15%以内，软件分析与有限元仿真分析滚子接触应力变化一致。

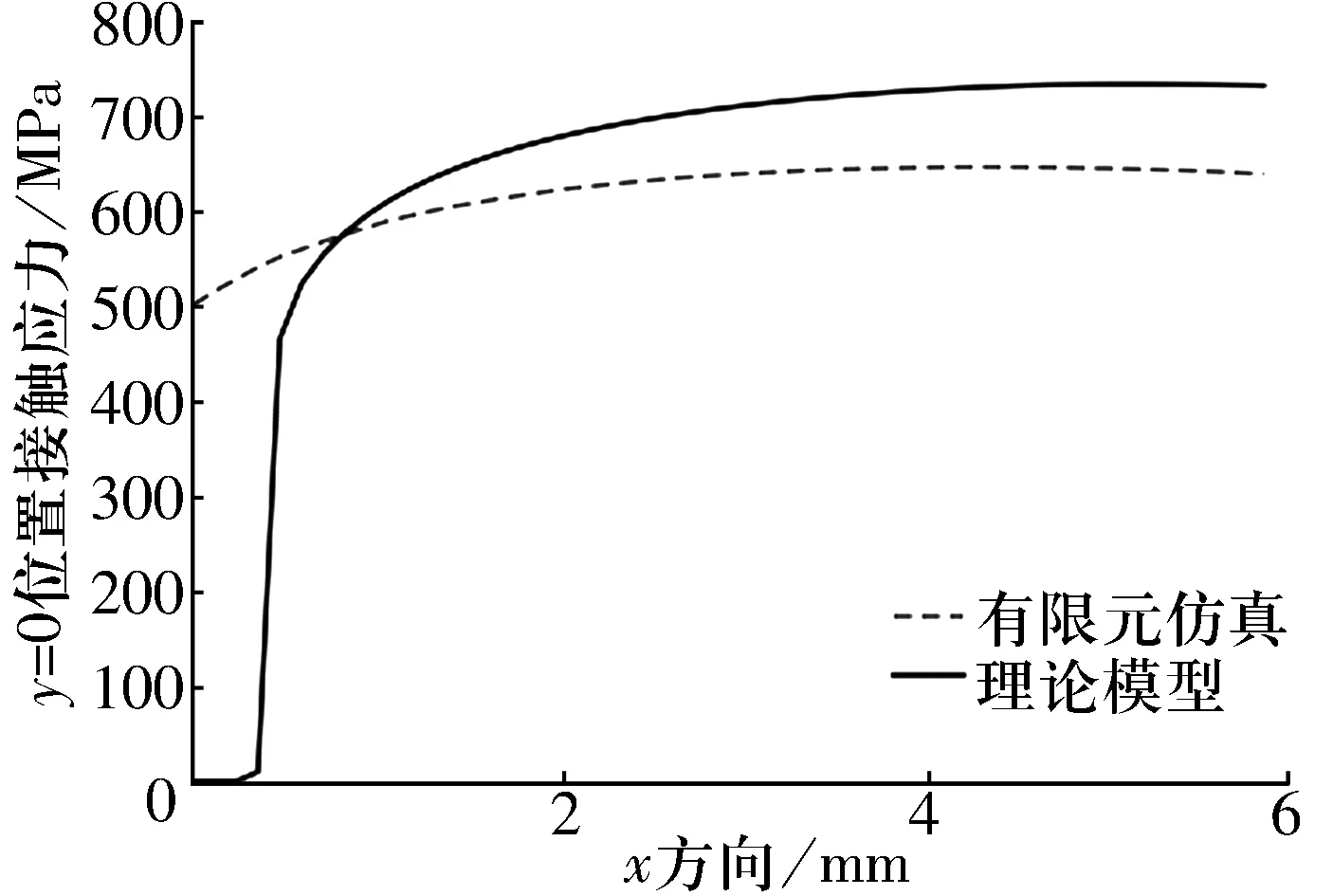
图14 Q=1 kN时对数形滚子接触应力

4 结束语

开发了圆锥滚子修形软件，提供直线型、圆弧型及对数型3种修形方式，可快速实现滚子修形曲线设计及接触应力分析，大大提高了滚子修形设计的工作效率。